广义Fitzhugh-Nagumo方程的无穷序列新解*

伊丽娜包俊东 套格图桑

（内蒙古师范大学数学科学学院，呼和浩特 010022）

广义Fitzhugh-Nagumo方程的无穷序列新解*

伊丽娜†包俊东 套格图桑

（内蒙古师范大学数学科学学院，呼和浩特 010022）

利用辅助方程的几种结论，构造了广义Fitzhugh-Nagumo方程的多种无穷序列新解.步骤一，利用函数变换与首次积分，给出了辅助方程的新解、Bäcklund变换和解的非线性叠加公式.步骤二，通过函数变换，将广义Fitzhugh-Nagumo方程的求解问题转化为非线性常微分方程的求解问题.步骤三，利用符号计算系统Mathematica与辅助方程的几种结论，构造了广义Fitzhugh-Nagumo方程的多种无穷序列新解.

广义Fitzhugh-Nagumo方程， 辅助方程， 首次积分， 无穷序列新解

引言

在孤立子理论中给出试探函数法、辅助方程法、同伦映射法和Bäcklund变换法等方法，构造了具任意次非线性项的非线性发展方程的新精确解［1-7］.比如：文献［1］用试探函数法，构造了广义mKdV方程（1）的新解.文献［2］用同伦映射法，构造了任意次非线性项的非线性发展方程（2）的新精确解

这里α，β，γ是任意非零常数，p，q，r非负常数，n是非零任意常数.

文献［3-6］用辅助方程法与Bäcklund变换法，构造了广义BBM方程和广义Zakharov-Kuzentsov方程的新精确解

这里α，β，γ，s，δ，ρ是常数，p是非零常数.

文献［7］用试探函数法，构造了广义Fitzhugh-Nagumo方程（6）的指数函数型新解这里v，k和p是任意非零常数.

本文用一种辅助方程的几种结论，构造了广义Fitzhugh-Nagumo方程的多种无穷序列新解.步骤一，利用函数变换与首次积分，给出了辅助方程的新解、Bäcklund变换和解的非线性叠加公式.步骤二，通过函数变换，将广义Fitzhugh-Nagumo方程的求解问题转化为非线性常微分方程的求解问题.步骤三，利用符号计算系统Mathematica与辅助方程的几种结论，构造了广义Fitzhugh-Nagumo方程的由双曲函数、Jacobi椭圆函数、Riemannθ函数、三角函数和有理函数组成的多种无穷序列新解.这些解包括了光孤立子解、尖锋孤立子解和紧孤立子解.

1 辅助方程的几种结论

下面给出辅助方程的几种新结论，并构造广义Fitzhugh-Nagumo方程的多种无穷序列新解

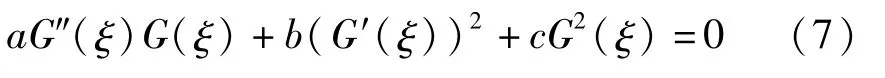
其中a，b，c是常数.

1.1 辅助方程与首次积分

通过函数变换，可以把二阶非线性常微分方程（7）转化为一阶常微分方程组

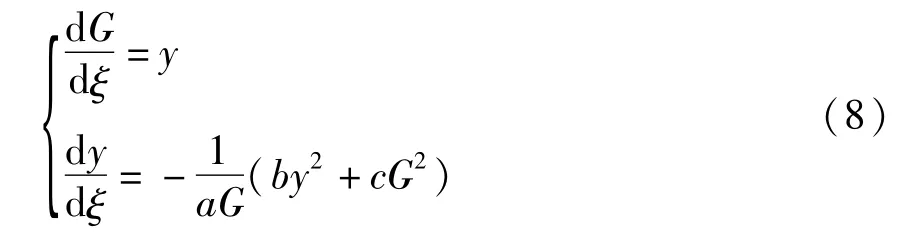
通过函数变换（9），把一阶常微分方程组（8）转化为一阶常微分方程组（8）

经计算获得了一阶常微分方程组（10）的如下首次积分

这里m是任意常数.

把（11）式代入常微分方程组（10）的第一方程后得到下列常微分方程

1.2 辅助方程的解与Bäcklund变换

下面在三种情况下，获得了辅助方程（12）的新结论.

情况1.当b＝0时，方程（12），通过下列变换，转化为Riccati方程（14）

情况2.Riccati方程（15）的解

经计算获得了Riccati方程（15）的下列解

这里d1，d2是任意常数.

情况3.Riccati方程（15）的Bäcklund变换.

若Z（τ）是Riccati方程（15）的非常数解，则下列也是Riccati方程（15）的解

这里A，B，C，d是不全为零的任意常数.

情况4.当b＝0时，方程（12）存在如下解

情况5.当b＝0时，若G（τ）是辅助方程（12）的非常数解，则下列也是辅助方程（12）的解

这里f，h，s是不全为零的任意常数.

情况6.当b＝a时，若G（τ）是第二种辅助方程（12）的解，则下列也是第二种辅助方程（12）的解

情况7.当b＝a时，方程（12）存在如下Jacobi椭圆函数解

情况9.当a＝-2b时，方程（12）通过下列变换（35），转化为Riccati方程（36）

情况10.Riccati方程（36）的Bäcklund变换.

若U（τ）是Riccati方程（36）的解，则也是Riccati方程（36）的解

其中P，Q，S是不全为零的任意常数.

情况11.Riccati方程（36）的解

这里d1是任意常数.

1.3 辅助方程与Riccati方程的Bäcklund变换

辅助方程（7）通过函数变换（39），转化为Riccati方程（40）

根据文献［9］～［11］中给出的有关结论，可以获得Riccati方程（40）的解、Bäcklund变换和解的非线性叠加公式（未列出）.因而，通过函数变换（39），获得辅助方程（7）的无穷序列解.

2 广义Fitzhugh-Nagumo方程的多种无穷序列新解

下面用辅助方程的几种结论，构造广义Fitzhugh-Nagumo方程的由Jacobi椭圆函数和Riemannθ函数等函数构成的多种无穷序列新解.

将u（x，t）＝u（ξ），ξ＝μx+ωt（这里μ和ω是待定常数），代入广义Fitzhugh-Nagumo方程（6）后得到下列非线性常微分方程

在非线性常微分方程（41）中进行如下函数变换（42）后得到非线性常微分方程（43）.

选择非线性常微分方程（43）的如下形式解，构造广义Fitzhugh-Nagumo方程（6）的新解

这里g0，g1和g2是待定常数.

将形式解（44）与辅助方程（7）一起代入非线性常微分方程（43），并令Gj（ξ）（G′（ξ））i（i＝0，1，2，3，…，7，8；j+i＝8）的系数为零后得到一个g0，g1，g2，a，b，c，μ，ω为未知量的非线性代数方程组（未列出）.利用符号计算系统Mathematica求出该方程组的如下解

在（45）～（50）中（a+b）c＜0.

将代数方程组的解（45）～（50）分别与形式解（44）一起代入（42）式后获得Fitzhugh-Nagumo方程（6）的如下形式解

2.1 无穷序列光滑孤立子新解

根据文献［9］～［11］中给出的有关结论，可以获得Riccati方程（40）的解、Bäcklund变换和解的非线性叠加公式（未列出）.利用这些结论与关系式（39）和（40），构造Fitzhugh-Nagumo方程的无穷序列新解.这里包括双曲函数、三角函数和有理函数组成的光滑孤立子解.比如：通过下列叠加公式，可以获得双曲函数无穷序列新解

这里A，B，C，d是不全为零的任意常数.

2.2 无穷序列类孤子新解

当b＝0，b＝a和a＝-2b时，通过形式解（51）～（56），获得Fitzhugh-Nagumo方程的Riemannθ函数型、Jacobi椭圆函数型、双曲函数型、三角函数型和有理函数型无穷序列新解.下面用形式解（55），构造无穷序列类孤子新解.

情形1.当b＝0时，通过下列叠加公式，构造双曲函数型无穷序列类孤子新解

这里A，B，C，d是不全为零的任意常数.

情形2.通过下列叠加公式，构造Fitzhugh-Nagumo方程的指数函数型无穷序列尖锋孤立子新解

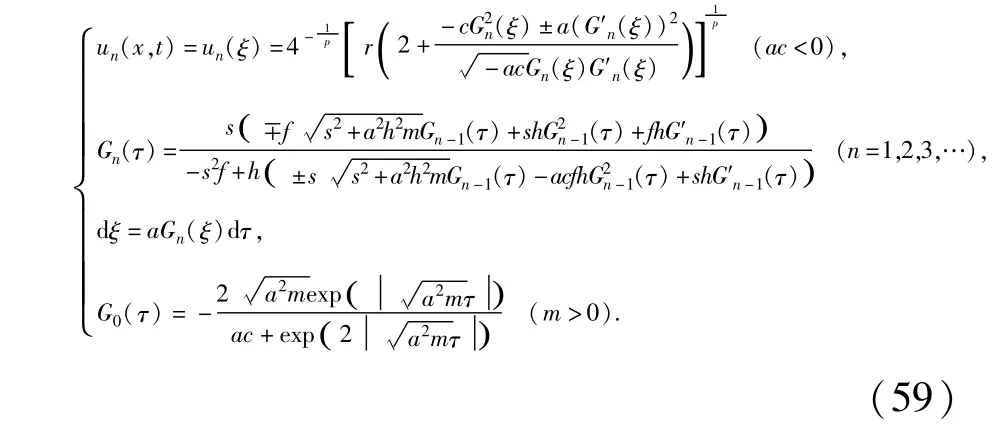
这里f，s，h是不全为零的任意常数.

情形3.当b＝a时，通过下列叠加公式，构造Fitzhugh-Nagumo方程的Jacobi椭圆函数型无穷序列新解

情形4.当b＝a时，通过下列叠加公式，构造Fitzhugh-Nagumo方程的Riemannθ函数型无穷序列新解

情形5.当a＝-2b时，通过下列叠加公式，构造Fitzhugh-Nagumo方程的有理函数型无穷序列新解

其中P，Q，S是不全为零的任意常数，d1是任意常数.

3 结论

文献［1］～［7］用辅助方程法和试探函数法，获得了具任意次非线性项发展方程的由双曲函数、三角函数和有理函数组成的有限多个新解.本文在辅助方程法［3-15］的基础上，给出二阶非线性常微分方程的相关结论，构造了广义Fitzhugh-Nagumo方程的由双曲函数、Jacobi椭圆函数、Riemannθ函数、三角函数和有理函数组成的多种无穷序列新解.这些解包括了光孤立子解、尖锋孤立子解和紧孤立子解.

1 Fu Z T，Chen Z，Liu SK，Liu SD.New solutions to Generalized mKdV equation.Communnications in Theoretical Physics（Beijing），2004，42（1）：25～28

2 莫嘉琪，张伟江，陈贤峰.强非线性发展方程孤波同伦解法.物理学报，2007，56（11）：6169～6172（Mo JQ，ZhangW J，Chen X F.The homotopic solving method of solitary wave for strong nonlinear evolution equation.Acta Physica Sinica，2007，56（11）：6169～6172（in Chinese））

3 Zheng X D，Chen Y，Li B，Zhang H Q.A new Generalization of extended tanh-function method for solving nonlinear evolution equations.Communnications in Theoretical Physics（Beijing），2003，39：647～652

4 Taogetusang，Sirendaoerji.New exact solitary wave solutions to generalized mKdV equation and generalized Zakharov-Kuzentsov equation.Chinese Physics B，2006，15（6）：1143～1148

5 Chen Y，Li B，Zhang H Q.Bäcklund transformation and exact solutions for a new Generalized Zakharov-Kuzentsov equation with nonlinear terms of any order.Communnications in Theoretical Physics（Beijing），2003，39（2）：135～140

6 Chen Y，Li B.New exact travellingwave solutions for Generalized Zakharov-Kuzentsov equations Using general pro-jective Riccatiequationmethod.Communnications in Theoretical Physics（Beijing），2004，41（1）：1～6

7 Liu C P，Chen JK，Cai F.A direct algebraicmethod finding particular solutions to some nonlinear evolution equations.Communnications in Theoretical Physics（Beijing），2004，42（1）：74～78

8 王军民.修正的Korteweg de Vries-正弦Gordon方程的Riemannθ函数解.物理学报，2012，61（8）：080201（1～5）（Wang JM.Riemannθfunction solutions to modified Korteweg de Vries-sine-Gordon equation.Acta Physica Sinica，2012，61（8）：080201（1～5）（in Chinese））

9 套格图桑，白玉梅.非线性发展方程的Riemann theta函数等几种新解.物理学报，2013，62（10）：100201（1～9）（Taogetusang，Bai Y M.Riemann theta function and other several kinds of new solutions of nonlinear evolution equations.Acta Physica Sinica，2013，62（10）：100201（1～9））（in Chinese））

10 Taogetusang，Sirendaoerji，Li SM.Infinite Sequence Soliton-like Exact Solutions of The（2+1）-dimensional Breaking Soliton Equation.Communnications in Theoretical Physics（Beijing），2011，55（6）：949～954

11 Taogetusang，Sirendaoerji，Li S M.New application to Riccatiequation.Chinese Physics B，2010，19（8）：080303（1～8）

12张文玲，马松华，陈晶晶.（2+1）维Korteweg-de Vries方程的复合波解及局域激发.物理学报，2014，63（8）：080506（1～7）（ZhangW L，Ma SH，Chen JJ.Complex wave solutions and localized excitations of（2+1）-dimensional korteweg-de Vries system.Acta Physica Sinica，2014，63（8）：080506（1～7）（in Chinese））

13 Khaled A.Gepreel，Saleh Omran.Exact solutions for nonlinear partial fractional differential equations.Chinese Physics B，2012，21（11）：110204（1～7）

14 Md Nur Alam，Md Ali Akbar，Syed Tauseef Mohyud Din.A novel G′（ξ）／G（ξ）-expansion method and its application to the Boussinesq equation.Chinese Physics B，2014，23（2）：020203（1-10）

15 Xie F D，Chen J，LüZ S.Using symbolic computation to exactly solve the integrable Broer-Kaup equations in（2+1）-dimensional spaces.Communnications in Theoretical Phys-ics，2005，43（4）：585～590

NEW INFINITE SEQUENCE SOLUTIONSOF THE GENERALIZED FITZHUGH-NAGUMO EQUATION*

Yi Lina†Bao Jundong Taogetusang
（The College of Mathematical Science，Inner Mongolia Normal University，Huhhot010022，China）

According to several conclusions of auxiliary equation，the new infinite sequence solutions of the generalized Fitzhugh-Nagumo equation is constructed in this paper.Firstly，the function transformation and the first integral are presented to obtain the new solutions，Bäcklund transformation and the nonlinear solution superposition formula of the auxiliary equation.Secondly，through the function transformation，the problem to gain the solutions of the generalized Fitzhugh-Nagumo equation is changed to the problem of obtaining the solutions of the nonlinear ordinary differential equations.Thirdly，some conclusions of the auxiliary equation are employed to construct various new infinite sequence solutions of the generalized Fitzhugh-Nagumo equation with the help of symbolic computation system‘Mathematica’.

generalized Fitzhugh-Nagumo equation， auxiliary equations， first integral， new infinite sequence solutions

10.6052／1672-6553-2015-77

2015-9-28收到第1稿，2015-10-20收到修改稿.

*国家自然科学基金（11361040）、内蒙古自治区自然科学基金（2015MS0128）、内蒙古自治区高等学校科学研究基金（NJZY16180）、内蒙古自治区2016年硕士研究生科研创新项目（S20161013502）和内蒙古师范大学研究生科研创新基金项目（CXJJS16081）资助的课题

†通讯作者E-mail：573028703＠qq.com

Received 28 September 2015，revised 20 October 2015.

*The project supported by the Natural Natural Science Foundation of China（11361040），the Natural Science Foundation of Inner Mongolia Autonomous Region，China（2015MS0128），the Science Research Foundation of Institution of Higher Education of InnerMongolia Autonomous Region，China（NJZY16180），the Inner Mongolia autonomous region in 2016 graduate student scientific research innovation projects（S20161013502）and the Inner Mongolia normal university graduate student scientific research innovation fund projects（CXJJS16081）

†Corresponding author E-mail：573028703＠qq.com