偏角不对中轴系振动的工艺控制措施研究*

李永哲王德石 周奇郑

（海军工程大学兵器工程系，武汉 430033）

偏角不对中轴系振动的工艺控制措施研究*

李永哲†王德石 周奇郑

（海军工程大学兵器工程系，武汉 430033）

考虑非线性非稳态油膜力、局部碰摩力和质量不平衡的耦合激励，建立偏角不对中轴系非线性动力学方程，数值模拟并分析不对中偏角量对系统振动特性的影响，根据计算结果制定不对中偏角量的工艺控制标准.仿真计算研究表明：非稳态油膜力激励下，轴系动力学方程形式繁琐，求解困难，导致系统产生复杂的动力学行为，难以通过理论分析有效控制轴系非线性振动，而通过制定工艺可以避免理论研究难题，达到控制非线性振动级别的目的.

非线性振动， 振动控制， 工艺措施， 偏角不对中， 非稳态油膜力

引言

由于制造、加工和安装误差，轴承架的不均匀热膨胀及转子质量不平衡等原因，致使旋转机械轴系中必然存在不对中现象.偏角不对中是轴与轴之间的连接存在偏斜量，是造成旋转机械故障的重要根源.轴系存在偏角不对中会造成油膜失稳、转子与定子碰摩、轴挠曲变形、联轴器偏转、轴承断裂等严重危害.最终导致机械设备强烈振动，影响旋转机械正常工作的稳定性［1］.因此，揭示偏角不对中轴系振动特性，研究振动控制工艺措施，对于提高旋转机械故障诊断和预测水平以及治理轴系振动具有重要意义.

多年来，国内外学者对轴系不对中进行了大量的研究.较早时期，陆钟等［2］就对凸缘联轴节转子不对中现象进行动力学分析，以获得系统故障发生机理，研究推导出参数，强迫激励下的系统动力学方程，并使用Fourier级数展开法求解方程获得系统稳态运动解.文献［3］考虑转子系统分别存在交角不对中和平行不对中两种情况，分析和比较两种状态下系统的扭转振动响应特征.不对中会产生附加力和力矩，Sekhar等［4］给出了附加力和力矩的数学表达式，推导了不对中转子系统模型，指出了系统振动特性与附加力和力矩激励位置密切相关.Al-Hussain等［5］以刚性联接平行不对中转子为研究对象，数值模拟了系统横向和扭转振动特性，给出了其振动产生的激励源.冯昌林［6-7］考虑万向铰传动的偏斜轴系，建立系统横向振动数学模型并进行稳定性分析，采用希尔行列式法获得共振稳定图，并分析系统参数对系统稳定性的影响.周奇郑等［8］考虑非稳态油膜力、转子与定子碰摩及非稳态油膜力因素的耦合作用，推导了不对中轴系的横向振动微分方程.数值模拟了系统在加速运动过程，分析了系统的横向振动特性与系统参数的关系.

现有文献主要是通过揭示偏角不对中轴系的复杂振动特性，探究振动控制机理，利用理论分析达到控制轴系振动的目的.然而由于轴系是复杂的振动系统，理论上的分析以及振动响应也十分复杂，故仅仅依靠理论分析难以降低轴系振动级别.为此，本文提出避开理论研究难题，通过制定工艺，控制偏角不对中轴系进行非线性振动分析.

1 动力学模型

基于文献［8］中的偏角不对中轴系动力学方程，考虑非稳态油膜力、局部碰摩力及不平衡质量耦合作用，建立系统动力学模型（如图1所示）.图1中，主动轴O1的初始旋转速度为φ′0，通过刚性联轴器联接从动轴O2，主、从动轴的轴心线之间存在偏斜现象，产生不对中偏角量α.转盘1和转盘2分别在主、从动轴的中心位置处，承载主、从动轴的全部质量m1和m2.以垂直于主动轴O1轴心线的平面作为参考平面，建立轴系静平衡参考坐标系oxy（如图2所示）.图2中，转盘1中心的坐标位置为O1（x1，y1），质心坐标位置为O′1（x′1，y′1），质量为m1，质量偏心距为ε1，与x轴夹角为φ1.转盘2的坐标位置为O2（x2，y2），质心坐标位置为O′2（x′2，y′2），质量为m2，质量偏心距为ε2，与x轴夹角为φ2.将主、从动轴的刚度、阻尼等效到转盘1和转盘2处，K1、K2、D1、D2分别为两转盘处转轴的等效刚度与阻尼，fx和Fx分别为作用在主动轴上的非稳态油膜力和局部碰摩力.

图1 偏角不对中轴系动力学模型Fig.1 The dynamicalmodel ofthe shafting with angularmisalignment

图2 轴系参考坐标系Fig.2 Coordinate system of the shafting

1.1 轴系动力学方程

取轴颈平均间隙cz＝0.2mm，引入无量纲参数如下所示：

式中，记（）′＝d（）／dτ，（）″＝d（）／dτ2.建立非稳态油膜力激励下的偏角不对中轴系的横向振动微分方程：

1.2 非稳态油膜力

由文献［9］列出非稳态油膜力：

式中，σ＝μωRL（R／cz）2（L／2R）2为Sommerfeld修正数，μ为粘度系数，ω为转轴转速，L为轴承长度，R为轴承半径.

无量纲油膜力分量为

式中，X、Y分别为轴颈中心在x、y方向上的无量纲位移分量分别为轴颈中心在x、y方向上的无量纲速度分量，其中，

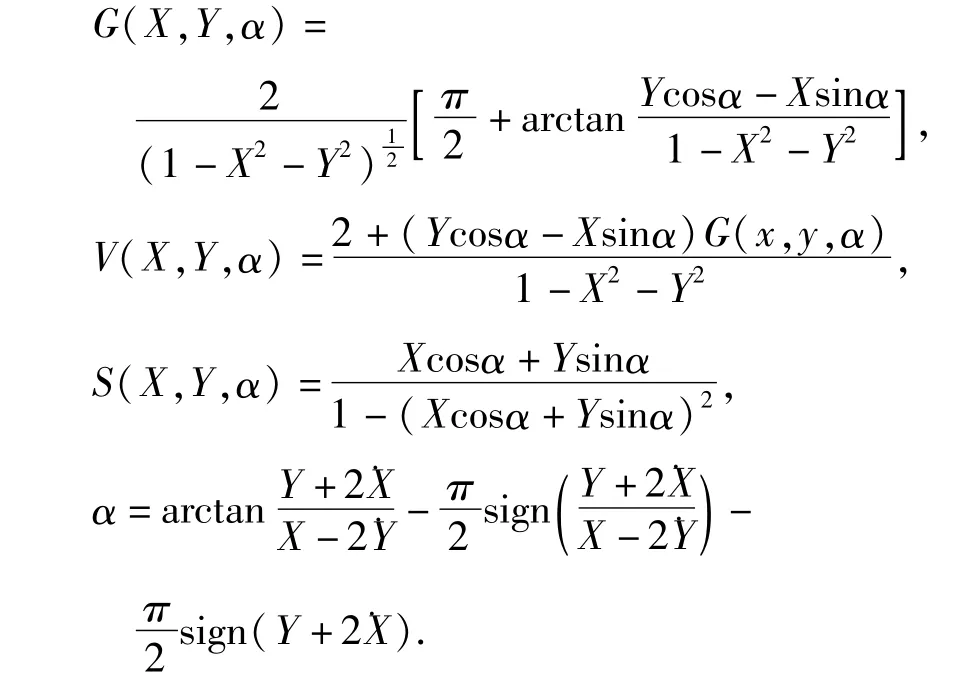
1.3 局部碰摩力

由文献［10］给出局部碰摩力表达式：

式中，k为定子径向刚度为转子轴心的径向位移，E0为转子、定子间初始间隙.

碰摩力在o-xy坐标系上的分量为：

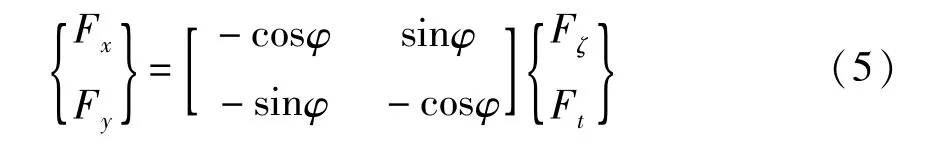
将式（4）代入式（5）中可得局部碰摩力分量为：

式中，f为不考虑速度影响时的摩擦系数，b为速度影响因子，n为速度项的次数.

根据式（1）可知，由于非线性油膜力和局部碰摩力的激励，偏角不对中轴系振动微分方程是非线性非齐次三阶变系数的常微分方程，其中含有许多几何和运动耦合项，形式复杂，难以求出解析解.系统动力学方程的非线性和复杂性，就决定了系统复杂的振动特性.

2 轴系振动特性分析

计算时取图1所示系统的结构参数为m1＝50kg，η＝0.8，D1＝D2＝0，μ＝0.0373N·s·m-2，cz＝0.2mm，φ0＝0rad.采用Runge-Kutta法对式（1）进行数值积分.取不对中偏角量α＝0～5×10-4，分析轴系的振动特性.

图3 当ω＝0.8，m′＝0.8时，无量纲位移X1的分岔图Fig.3 The bifurcation diagrams ofX1whenω＝0.8，m′＝0.8

由分岔图3可知：当ω＝0.8时，在α＝0～5× 10-4整个范围内，Poincare截面上呈现为模糊一片的散点集，说明轴系振动响应存在混沌运动.比较图5（a）和5（b）可知，在不对中偏角量一定时，转轴质量偏心的改变并没有改变系统的振动特性.

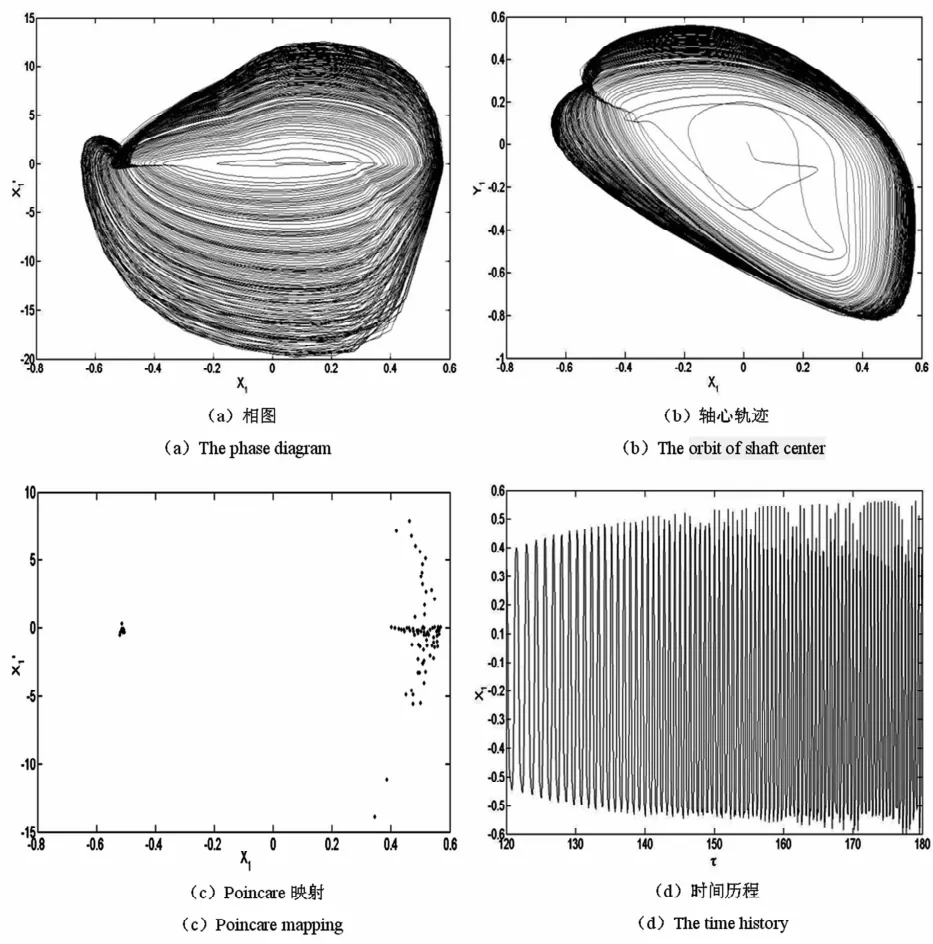
图4 ω＝0.8，α＝3.6×10-4时系统振动响应Fig.4 The vibration response of the system whenω＝0.8 and α＝3.6×10-4

由图4可知，当取系统参数ω＝0.8，ε1＝ε2＝0.04及α＝3.6×10-4时，系统在τ＝120～180范围内表现为混沌运动.表现为相轨迹和轴心轨迹为局限于有界区域内的复杂不封闭曲线，Poincare截面映射图4（c）为一些散点集，时间历程图呈现随机信号的特征.此时，系统平均振动幅值为X1A＝0.3030，最大振动幅值为X1M＝0.5457.

不考虑非线性非稳态油膜力和局部碰摩力激励，仍取偏角不对中量α＝0～5.0×10-4，分析轴系的振动特性.

比较分岔图3和分岔图5（a）可知，不考虑非线性作用力激励时，轴系在α＝0～5.0×10-4整个范围内仍然做概周期运动或混沌运动.又由图5（b）可得，在α＝0.65～1.00范围内，分岔图上显示为孤立的点.说明此时系统做倍周期运动，退出混沌状态，但是此时系统振动幅度显著增加.

图5 无量纲位移X1的分岔图Fig.5 The bifurcation diagrams ofX1

由振动响应图6可知，忽略非线性作用力，系统取不对中偏角量为α＝5×10-5时，轴系仍然表现为混沌运动.

图6 系统振动响应Fig.6 The vibration response of the system

综上所述，无论是否考虑非线性油膜力和局部碰摩力激励，系统在不对中偏角的作用下，都会产生复杂的混沌运动，说明不对中偏角决定了系统振动特性，并且系统振动幅度随不对中偏角量改变成无规律变化.

3 轴系振动控制工艺分析

取系统参数质量偏心距ε1＝0.1，ε2＝0.2，旋转轴系质量比m′＝0.8，主动轴无量纲角速度ω＝0.8，改变不对中偏角量，计算得到相应的偏角不对中轴系振动响应的平均振动幅值X1A和最大振动幅值X1M，如表1所示.

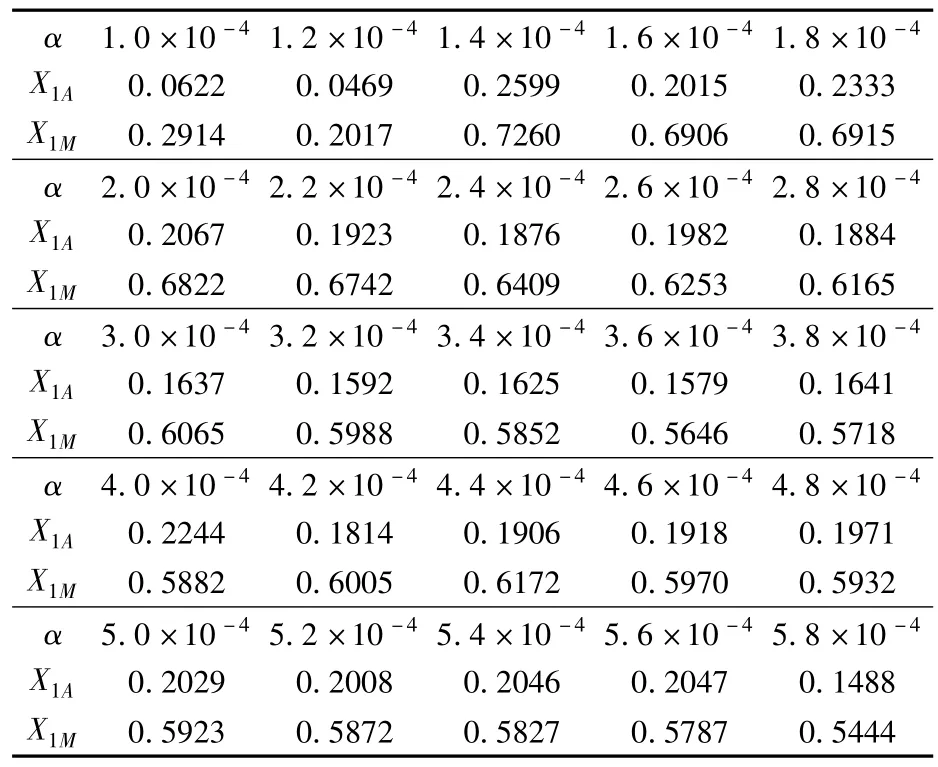
表1 对应不同偏角量的系统振动幅值Table 1 The system vibration amplitude corresponding to different anglemisalignment

根据表1所示数据，绘制出系统振动响应幅值随不对中偏角量的变化曲线，如图7所示.

图7 系统振动幅值与偏角量变化关系曲线Fig.7 Therelationship of the system vibration amplitude and anglemisalignment

由表1数据和图7变化曲线可以看出，系统振动幅度随不对中偏角量改变成无规则变化.当α＝1.2×10-4时，系统振动响应幅值最小，即α＝1.2× 10-4是系统最优偏角量.

忽略非线性油膜力和局部碰摩力激励，在相同系统参数下，计算得到相应于不同不对中偏角量的轴系平均振动幅值XA和最大振动幅值XM，如表2所示.

根据表2所示的数据，绘制出系统振动响应幅值随不对中偏角量的变化曲线，如图8所示.

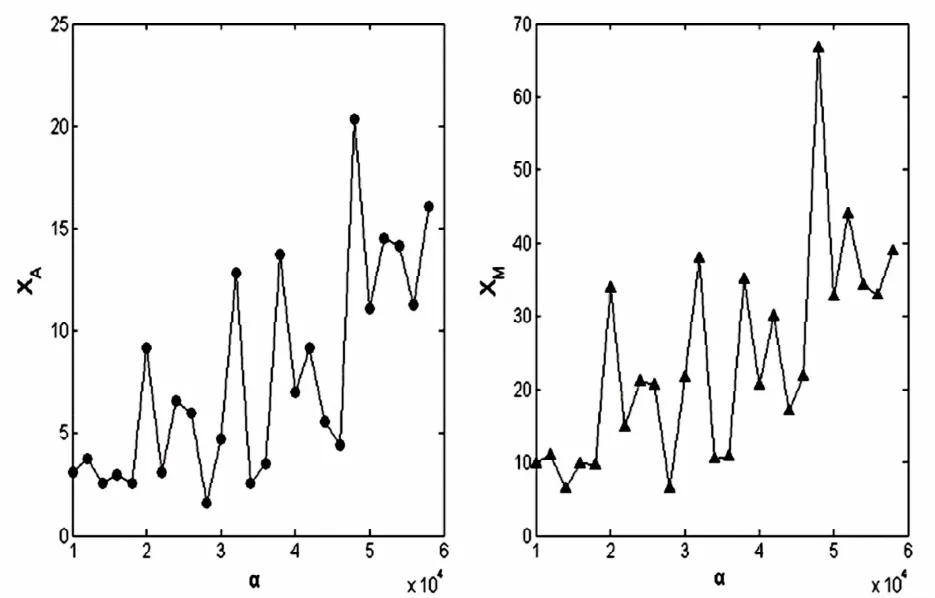
图8 系统振动响应幅值与不对中偏角量的关系变化曲线Fig.8 Therelationship of the system vibration amplitude and anglemisalignment

由表2和图8可知，当忽略非线性作用力激励时，随着不对中偏角增大，轴系振动幅度依然成无规则变化，并且与图7所示情况不同.微小的不对中偏角量的变化会引起系统振动幅度较大的改变.又比较表1和表2的数据结果易得，考虑非稳态油膜力激励的情况下，系统振动水平降低1至2个数量级.说明非稳态油膜力显著地降低了系统的振动级别.并且当不对中偏角量为α＝1.2×10-4时，系统振动响应幅值最小.因此在工艺上，应使轴系的不对中偏角量为α＝1.2×10-4，以最大限度地降低系统振动，保证机械运行的稳定性.

4 结论

（1）由于非线性油膜力和局部碰摩力的激励，偏角不对中轴系振动微分方程是非线性非齐次三阶变系数的常微分方程，其中含有许多几何和运动耦合项，形式复杂，难以求出解析解.

（2）非线性力激励下偏角不对中轴系呈现出更为复杂的振动特性.表现为：系统振动响应包括概周期运动、混沌运动等复杂非线性动力学行为.系统振动幅值随不对中偏角量的变化成无规则改变，但微小的参数变化却可以较大改变系统振动水平.

（3）非稳态油膜力的存在，没有改变偏角不对中轴系的复杂振动特性，但有效地降低了系统振动级别.

（4）由于存在非线性力激励，偏角不对中轴系动力学方程形式繁琐，求解困难.系统的振动响应又是复杂的混沌，导致理论研究轴系非线性振动控制的困难.因此通过制定工艺可以避免复杂繁琐的理论分析，达到降低轴系振动级别的目的.

（5）工艺上，应选择不对中偏角量为α＝1.2 ×10-4的轴系，以有效降低系统振动，确保机械运行稳定.

1 Jack SC.Successful shaft hot-alignment.Hydrocarbon Processing，1969，39：110～123

2 陆钟，李惠昌.转子不对中故障的振动特性和试验.上海机械学院学报，1987，9（3）：49～53（Lu Z，LIH C.Vibration characteristics and the test ofmisaligned rotors.Journal of ShangHai Institute of Mechanical Engineering，1987，9（3）：49～53（in Chinese））

3 黄典贵，蒋滋康.交角不对中转子系统的扭振特性分析.汽轮机技术，1995，37（3）：150～152（Huang D G，Jiang Z K.Torsional vibration analysis of rotor system with angle misalignment.Turbine Technology，1995，37（3）：150～152（in Chinese））

4 Sekhar A S，Prabhu B S.Effects of coupling misalignmenton vibrations of rotating machinery.Journal of Sound and Vibration，1995，185（4）：655～671

5 Al-Hussain K M，Redmond I.Dynamic response of two rotors connected by rigid mechanical coupling with parallel misalignment.Journal of Sound and Vibration，2002，249（3）：483～498

6 冯昌林，朱拥勇，王德石.万向铰传动偏斜轴系横向振动的主共振分析.舰船科学技术，2011，33（10）：17～20（Feng C L，Zhu Y Y，Wang D S.Principal resonance analysis on lateral vibration ofmisaligned shafting driven by universal joint.Ship Science And Technology，2011，33（10）：17～20（in Chinese））

7 冯昌林，王德石，朱拥勇.过度过程中万向铰传动偏斜轴系的横向振动分析.船舶力学，2012，16（11）：1314～1320（Feng C L，Zhu Y Y，Wang D S.Lateral vibration analysis of misaligned shafting driven by a universal joint during transient process.Journal of Ship Mechanics，2011，33（10）：17～20（in Chinese））

8 周奇郑，王德石，张恺.加速过程偏角不对中轴系横向振动特性研究.动力学与控制学报，2014，12（4）：315～320（Zhou Q Z，Wang D S，Zhang K.Lateral vibration characteristics analysis of shafting with angle misalignment in accelerating process.Journal of Dynamics and Control，2014，12（4）：315～320（in Chinese））

9 张文.转子动力学理论基础.北京：科学出版社，1990（Zhang W.Rotor dynamics theory foundation.BeiJing：Science Publishing，1990（in Chinese））

10 丁千，陈予恕.转子碰摩运动的非稳态分析.航空动力学报，2000，15（2）：191～195（Ding Q，Chen Y S.Nonstationary analysis of rotor／casing rubbing.Journal of Aerospace Power，2000，15（2）：191～195（in Chinese） ）

TECHNOLOGYCONTROL MEASURESOF SHAFTING VIBRATION W ITH ANGLE M ISALIGNMENT*

Li Yongzhe†Wang Deshi Zhou Qizheng
（Department ofWeaponry Engineering Naval University of Engineering，Wuhan430033，China）

Considering the coupling excitation of nonlinear unsteady oil film force，rub-impact forces and mass unbalance，the shafting nonlinear dynamic equationswith angularmisalignment is firstly proposed.And through numerical simulation，the effect of angularmisalignment level on the system vibration characteristics is also studied.Moreover，the technology control standard formisalignment angle value based on the calculation results is developed.Simulation results show that under the unsteady oil film forces excitation，shafting dynamic equations are complicated，and it is difficult to solve them.This leads to the complex dynamic behavior of the system，and makes it difficult to effectively control shafting nonlinear vibration by theoretical analysis.It can avoid theoretical research problems through the developed control process and achieve the purpose of controlling the nonlinear vibration level.

nonlinear vibration， vibration control， technology measures， angle misalignment， unsteady oil film force

10.6052／1672-6553-2015-83

2015-10-23收到第1稿，2015-11-5收到修改稿.

*国家自然科学基金资助项目（11372350）

†通讯作者E-mail：1084911058＠qq.com

Received 23 October 2015，revised 5 November 2015.

*The project supported by the National Natural Science Foundation of China（11372350）

†Corresponding author E-mail：1084911058＠qq.com