周期激励下四维非线性系统的簇发共存现象*

张晓芳吴 磊 毕勤胜

（江苏大学土木工程与力学学院，镇江 212013）

周期激励下四维非线性系统的簇发共存现象*

张晓芳†吴 磊 毕勤胜

（江苏大学土木工程与力学学院，镇江 212013）

在一个周期激励的四维非自治系统中，当激励的频率远小于系统的固有频率时，系统表现出了两时间尺度的动力学行为.将激励项定义为慢变参数，激励系统可以转化为广义自治系统.分析了广义自治系统平衡点的稳定性及其分岔条件.应用快慢分析法和转换相图，探讨了系统对应于不同初始条件的簇发现象及其产生机制，并对其中多种簇发共存的形成机理进行了讨论.同时，由于慢过效应的存在，簇发振荡的激发态和沉寂态的连接点和理论分析中的分岔点相比存在一定的滞后现象.

周期激励， 分岔， 簇发， 两时间尺度

引言

在非线性动力系统中，两时间尺度会导致系统产生复杂的动力学行为，因而受到国内外学术界广泛的关注［1-4］.其动力学行为通常表现为周期簇发（periodic bursting）［5-6］，即在一个周期过程中呈现出大幅振荡和小幅振荡的组合.大幅振荡可看作是快慢系统的激发态（spiking state）［7］.小幅振荡可看作是快慢系统的静息态（quiescent state）［8］.

近几十年来，国内外学者分别从理论分析和数值模拟等多方面对两时间尺度的动力学行为进行了研究.起初，人们通过将整个系统约化到单时间尺度上，给出系统的近似解［9］.随后，奇异摄动法被用来分析多时间尺度系统的解析解［10］.然而，这两种方法都无法深入探讨不同时间尺度相互影响下产生的复杂动力学特性.直到Rinzel提出了快慢分析法［11］，不同时间尺度之间的相互作用及其所导致的簇发振荡机理才得到很好的揭示.例如，利用该方法和几何分岔理论，Simo等［12］研究了双阱磁耦合电子振荡器组合系统的簇发振荡；Bertrain等［13］研究了具有双参Chay-Cook模型的簇发行为；Izhikevich［14］则提出了根据连接簇发态和静息态的两个分岔来命名不同簇发行为的方法，并给出了所有余维一分岔的簇发模式.到目前为止，虽然在多时间尺度的研究领域取得了一定的成果［15］，但大多数成果都基于低维系统而展开的，对于高维系统中的两时间尺度问题则涉及较少.高维系统由于其自身的复杂性，如多平衡态共存［16-18］，使得系统所表现出的簇发行为也尤为复杂.所以，高维系统的多时间尺度问题还有待进一步深入探索.

本文针对一个周期激励的四维非线性系统，通过参数调节使得激励频率远小于系统的固有频率，系统具有频域上的两个时间尺度，从而表现出明显的快慢效应.应用快慢分析法重点分析不同初始条件下系统产生的簇发共存现象，揭示簇发产生的机理.同时，进一步探讨了簇发共存现象的产生机制.

1 系统模型及分岔分析

为探讨高维系统的复杂簇发行为，我们在Abooee等［19］提出的一个三维混沌系统的基础上增加一个控制项u，并引入周期激励，得到了一个新的四维非自治系统

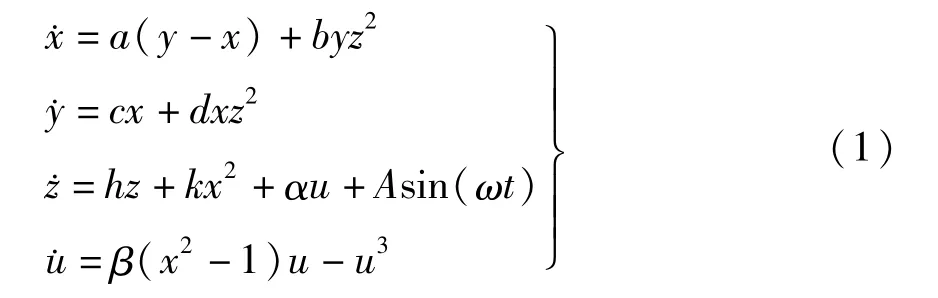
其中，A为激励幅值，ω为相应的激励频率.定义w＝Asin（ωt），系统（1）可转换为

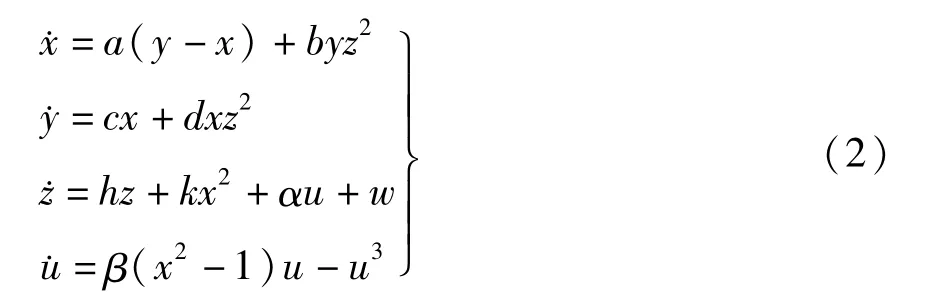
当激励频率ω远小于系统固有频率ΩN时，系统存在两个时间尺度.在每一个与固有频率有关的快变周期TN＝2π／ΩN中，激励项w＝Asin（ωt）在WA＝Asin（ωt0）和WB＝Asin（ωt0+2πω／ΩN）之间变化.由于ω／ΩN≪1，对于任意一个快变周期，激励项w变化很小，因此可以将其作为系统（2）的一个慢变参数.相应地，系统（2）可称之为广义自治系统，这样就可以应用传统的快慢分析法来揭示周期激励中不同簇发的产生机制.

当β＞0，c＞0，d＜0时，广义自治系统的平衡点可以表示为E0＝（0，0，-w／h，0），Ei±＝（xi0，yi0，zi0，0）以及Ej±＝（xj0，yj0，zj0，uj0），

其中，

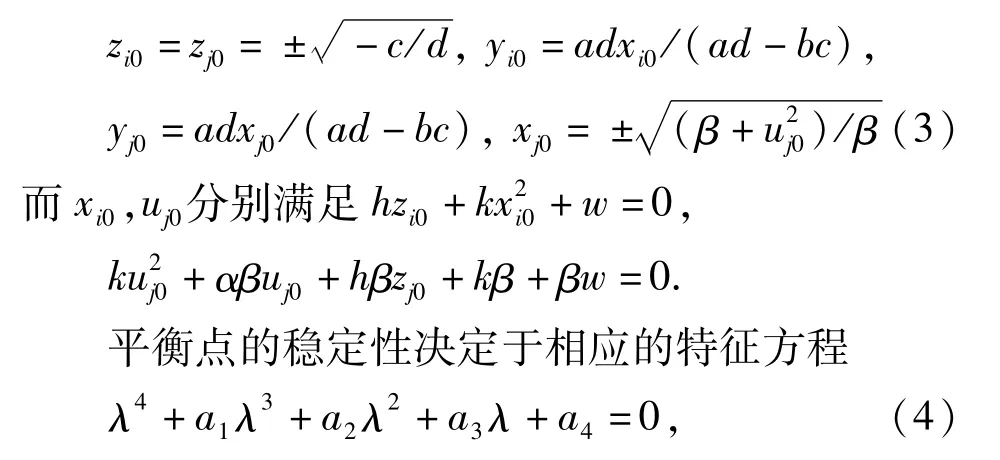
我们讨论E0的稳定性及其分岔条件.其中，E0所对应的特征方程的系数分别为

显然，E0发生简单分岔的条件为a4＝0，即

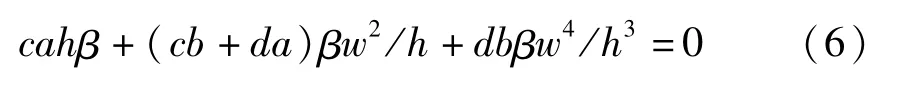
将λ＝iω0代入特征方程，可以得到E0产生Hopf分岔的条件为

由于表达式繁琐，就不在此列出.为了进一步讨论平衡点的稳定性及其分岔，将参数取定为a＝40.0，b＝1.0，c＝5.0，d＝-1.0，h＝-5.0，k＝-6.0，α＝1.0，β＝5.0，不难得到，E0＝（0，0，w／5，0）在w＝±11.180处产生简单分岔.并且，在11.180时稳定，E0在［-11.180，11.180］内不稳定，E0不满足产生Hopf分岔的条件.

同样方法也可以分析其他平衡点的稳定性及其分岔条件，只是比较繁琐，就不在此一一赘述，而是通过图1给出了所有的平衡点及其分岔产生出的极限环.图1（a）中，黄色、红色、蓝色和粉色曲线分别表示平衡点E0，E1±，E2±和E3±，其中实线表示平衡点稳定，虚线表示平衡点不稳定.图1（b）（c）（d）中的红色、蓝色和粉色曲线分别表示经过超临界Hopf分岔点H1±、H2±和H3±所产生的独立的极限环CYi±（i＝1，2，3）以及极限环CYi±碰撞所产生的大的极限环CYi（i＝1，2，3），各极限环的存在区间和存在形式详见表1.

图1 平衡点曲线图及其分岔产生出的极限环Fig.1 Equilibrium curves and limit cycles

表1 极限环的存在区间Table 1 The existence interval of limit cycles

2 周期激励下的簇发共存现象

在上述参数条件下，取定激励幅值A＝10.0，激励频率ω＝0.200，此时的激励频率远小于系统的固有频率，初始点分别取SP1（1.610，1.430，-2.240，2.820），SP2（1.400，1.250，-2.240，0.0），SP3（1.210，1.080，-2.240，-1.540）时，系统产生了不同簇发共存的现象.

2.1 初始点取SP1（1.610，1.430，-2.240，2.820）

图2给出了初始值取SP1（1.610，1.430，-2.240，2.820）时系统的时间历程图.从图中可以看出，系统产生了明显的簇发现象.

图2 初始点取SP1时簇发振荡的时间历程图Fig.2 Time historyof bursting oscillation for initial pointSP1

为了分析该簇发现象产生的机制，图3将平衡点曲线与转换相图进行了叠加.图3（a）给出了wx的二维叠加图，其中，红色实心圆点表示极限环CY1±和CY1.图3（b）给出了w-x-y的三维叠加图，红色曲线表示了w＝10.000时的极限环CY1.

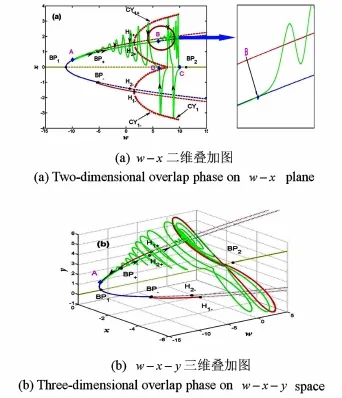
图3 初始点取SP1（1.610，1.430，-2.240，2.820）时系统平衡点曲线与转换相图的叠加Fig.3 Overlap of equilibrium curves and transformed phase onw-x-yspace for initial pointSP1（1.610，1.430，-2.240，2.820）

假定轨线自A点出发，由时间历程图可以判断，它将沿着稳定的平衡点E2+向右运动.当经过分岔点BP+（w＝-5.180）时，E2+失去其稳定性.需要说明的是，由于滞后现象的存在，轨线并没有立即跳跃，而是沿着不稳定的平衡点E2+走了一段路程，直至B（1.663，1.483，-2.222，0.101）点，此时w＝5.418.

经过B点后轨线向E1+跳跃，围绕平衡点E1+振荡，由于此时的E1+并不稳定，而在轨线的附近有由Hopf分岔而产生的稳定极限环CY1+存在，受到CY1+的吸引，轨线的振荡幅值迅速增大，系统由静息态进入激发态.随着w的增大，振荡的幅度也继续增加，直到w达到最大值10.000时，轨线到达C点.由图3（b）可知C点在大极限环CY1上，所以轨线沿着CY1运动到下半部分.之后受激励项w的影响，轨线围绕着极限环CY1开始向左运动直到D（0.0，0.029，-2.012，1.074）点，此时w＝6.135，广义自治系统中的极限环CY1消失，轨线回到CY1+的吸引域中，因此围绕着极限环CY1+振荡并继续向左运动.由于极限环逐渐缩小，振荡幅值也随之减小，直到穿过分岔点H1+，轨线退出激发态最终收敛于稳定平衡点E2+，回到初始点A，完成一个振荡周期.值得注意的是，在一个完整的簇发周期内，系统进入簇发态和退出激发态都是由于Hopf分岔引起的，因此我们将该簇发定义为非对称结构的Hopf／Hopf簇发.由于系统的对称性，当取初始点SP（-1.610，-1.430，-2.240，2.820）时，系统还存在一个和上述轨线关于x＝0.0平面对称的吸引子.

下面，要对轨线经过B点和D点后的运动方向作进一步探讨.由表1可知，在B点和D点处广义自治系统中有稳定的极限环CY1±，CY2，CY3同时存在.为了说明B点的运动趋势，我们将广义自治系统中的慢变参数w值取定为B点处对应值5.418，将（1.663，1.483，-2.222，0.101）作为初始条件，作出w＝5.418时广义自治系统的相图（见图4（a）），可见轨迹很快稳定到极限环CY1+上.由此可以说明此时的B点位于广义自治系统中极限环CY1+的吸引域内，所以系统轨线穿过B点之后受到CY1+的吸引，而逐渐趋向于CY1+.同样的方法，将w值取定为D点处的对应值6.135，以（0.0，0.029，-2.012，1.074）为初始条件作出广义自治系统的相图（见图4（b）），可以看出系统的轨迹很快稳定到极限环CY1+，说明D点同样位于广义自治系统中极限环CY1+的吸引域内，所以系统轨线穿过D点之后受到CY1+的吸引并逐渐趋向于CY1+.可见，轨线所处的吸引域决定了其运动方向.

图4 广义自治系统的相图Fig.4 Phase portrait of the generalized autonomous system

2.2 初始点取SP2（1.210，1.080，-2.240，-15.40）

取定初始点SP2（1.210，1.080，-2.240，-1.540），图5给出了系统的时间历程图.可以看出，相比较初始点SP1，系统的簇发行为发生了明显的变化.

图5 初始点取SP2时簇发振荡的时间历程图Fig.5 Time history of bursting oscillation for initial pointSP2

为了揭示该簇发现象产生的原因，图6展示了平衡点曲线与转换相图的叠加图，其中，图6（a）给出了w-x的二维叠加图，粉色实心原点表示极限环CY3±及其发生碰撞后产生的同样具有对称结构的大极限环CY3.图6（b）给出了w-x-y的三维叠加图，粉色曲线表示w＝9.443处的极限环CY3.由叠加图不难发现，相比较图3，系统的轨线在两个极限环CY3+和CY3-之间来回运动.

图6 初始点取SP2时系统平衡点曲线与转换相图的叠加Fig.6 Overlap of equilibrium curves and transformed phase onw-x-yspace for initial pointSP2

还是假定轨线从A点出发，沿着稳定的平衡点E2+向右运动.当经过分岔点BP+时，E2+失去其稳定性.由于滞后现象的存在，轨线没有立即跳跃，而是沿着不稳定的平衡点E2+走了一段路程，直至B（1.668，1.484，-2.228，-0.039）点，此时w＝5.552.

经过B点后轨线向E3+跳跃，围绕平衡点E3+振荡，由于此时的E3+同样不稳定，受到由Hopf分岔产生的稳定极限环CY3±发生碰撞后产生的大极限环CY3的吸引，轨线的振荡幅值迅速增大，系统由静息态进入激发态.随着w的增大，振荡的幅度也随之增大，直到w达到9.443时，轨线到达C点.由图6（b）可知C点在极限环CY3上，所以轨线围绕着CY3运动到下半部分.之后，轨线围绕大环CY3继续向右运动，直到运动到最右点w＝10.000，受激励项w的影响，轨线围绕极限环CY3开始向左运动.当运动到D（0.0，-0.016，-2.286，-1.257）点，此时w＝3.011，广义自治系统中的极限环CY3消失，且轨线运动到CY3-的吸引域中，因此围绕着极限环CY3-继续振荡并向左运动.随着极限环的逐渐减小，振荡幅值也随之减小，直到穿过分岔点H3-，轨线退出激发态最终收敛于稳定平衡点E2-，直到运动到最左点P（w＝-10.000），完成半个振荡周期.由于相空间的对称性，系统下半个周期的运动机理和上半个周期的运动机理相同，直到回到初始点A，完成一个周期振荡.这里，在一个完整的簇发周期内，轨线共经历了四个沉寂态和四个激发态，并且沉寂态和激发态同样是由Hopf分岔引起的，因而可以将其定义为对称式double-Hopf／Hopf簇发.

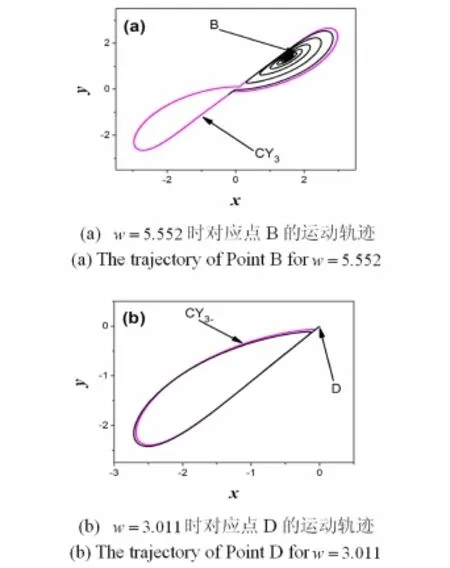
图7 广义自治系统的相图Fig.7 Phase portrait of the generalized autonomous system

同样方法可以说明轨线在经过B点和D点后的运动方向.由表1可知，在B点处广义自治系统中同时存在稳定的极限环CY1±，CY2，CY3，而在D点处广义自治系统中同时存在稳定的极限环CY1±，CY2±，CY3±.将广义自治系统中的w值取为B点处对应值5.552，将（1.668，1.484，-2.228，-0.039）作为初始条件，作出广义自治系统的相图（见图7（a）），可见轨迹很快稳定到极限环CY3上.由此说明B点位于广义自治系统中极限环CY3的吸引域内，所以系统轨线穿过B点之后受到CY3的吸引，而逐渐趋向于CY3.同样，将w值取为D点处对应值3.011，作出以（0.0，-0.016，-2.286，-1.257）为初始条件的广义自治系统的相图（见图7（b））.可以看出系统的轨迹很快稳定到极限环CY3-上，说明D点位于广义自治系统中极限环CY3-的吸引域内，所以系统轨线穿过D点之后受到CY3-的吸引并逐渐趋向于CY3-，从而运动到极限环CY3-上.

由此可见，在多个吸引子共存的情况下，系统的轨迹在运动过程中会穿过广义自治系统中不同吸引子的吸引域，从而受到不同吸引子的吸引，改变它的运动方向，导致了不同的簇发形式的产生.

2.3 初始点取SP3（1.400，1.250，-2.240，0.0）

取定初始点SP3（1.400，1.250，-2.240，0.0）.图8给出了系统的时间历程图.

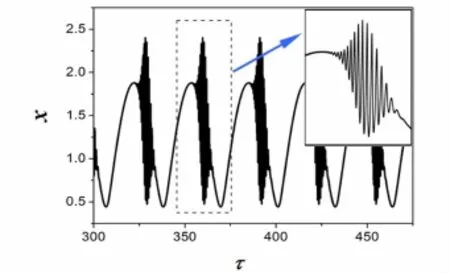
图8 初始点取SP3时的簇发振荡的时间历程图Fig.8 Time history of bursting oscillation for initial pointSP3

为了揭示该簇发现象产生的机制，图9将平衡点曲线与转换相图进行了叠加.其中，图9（a）给出了w-x的对称式二维叠加图，蓝色实心原点表示极限环CY2±.图9（b）给出了w-x-y的三维叠加图（上半支），蓝色曲线表示极限环CY2+.通过与图3和图6的比较不难发现，系统的轨线围绕单个吸引子振荡.

仍然假定轨线从A点出发，沿着稳定的平衡点E2+向右运动.当经过分岔点BP+时，E2+失去其稳定性并经过Hopf分岔点H2+产生极限环CY2+.由于滞后现象的存在，轨线没有因为失去稳定性而立即产生振荡，而是沿着不稳定的平衡点E2+走了一段路程，直到运动到最右点即w取得最大值10.000时向左折回运动才由于极限环CY2+的吸引开始振荡，由静息态进入激发态.当然，向右运动的整个过程中，系统的轨线没有发生跳跃的原因是因为轨线向右运动的整个过程中始终处于极限环CY2+吸引域中.之后，受到极限环CY2+的作用，随着w的减小，振荡幅度逐渐增大.当振荡幅值增大到极限环CY2+上时，轨线将围绕着该极限环继续向左运动，直到穿过分岔点H2+退出激发态，轨线受到稳定平衡点E2+的吸引，振荡幅值逐渐减小，最终收敛于稳定平衡点E2+，回到初始点A点，完成一个振荡周期.可以看出，整个周期振荡过程中，系统的簇发行为同样是由一个Hopf分岔点引起的，因此可以将其定义为Hopf／Hopf簇发.由于系统的对称性，当初始点取定为SP（-1.400，-1.250，-2.240，0.0）时，系统还存在一个和上述簇发振荡相对称的吸引子（见图9（a））.

图9 初始点取SP3时系统平衡点曲线与转换相图的叠加Fig.9 Overlap of equilibrium curves and transformed phase onw-x-yspace for initial pointSP3

3 结论

对于一个四维周期激励系统，当激励频率远小于原系统的固有频率时，系统存在两时间尺度，表现出明显的快慢效应，从而产生各种复杂的簇发现象.在特定的参数下通过对广义自治系统平衡点的分岔分析，发现了在某些参数条件下存在多个吸引子共存的现象.在相同激励幅值下取定不同的初始点，由于广义自治系统多吸引子的共存，随着初始点的变化，激励系统轨线运动到不同的吸引域，从而产生不同的簇发行为，得到不同的簇发形式.如非对称结构的Hopf／Hopf簇发，对称结构的double-Hopf／Hopf簇发以及Hopf／Hopf簇发.此外，滞后现象在簇发现象中表现的较为明显.

1 Dai H H，Yue X K，Liu C S.A multiple scale time domain collocation method for solving non-linear dynamical system.International Journal of Non-linear Mechanics，2014，67（1）：342～351

2 Kim S Y，Lim W.Thermodynamic order parameters and statistical-mechanical measures for characterization of the burstand spike synchronizations of bursting neurons.Physica A，2015，438（1）：544～559

3 Xu Jie，Miao Yu.Lp（p＞2）-strong convergence of an averaging principle for two-time-scales jump-diffusion stochastic differential equations.Nonlinear Analysis：Hybrid Systems，2015，18（1）：33～47

4 张艳娇，李美生，陆启韶.ML神经元的放电模式及时滞对神经元同步的影响.动力学与控制学报，2009，7（1）：019～5（Zhang Y J，Li M S，Lu Q S.Firing patterns and the effect of time-delay coupling on synchronization of two copuled chaotic ML neurons.Journal of Dynamics and Control，2009，7（1）：019～5（in Chinese））

5 Ferrari F A S，Viana G L，Lopes SR，et al.Phase synchronization of coupled bursting neurons and the generalized Kuramotomodel.Neural Networks，2015，66（1）：107～118

6 Teerawat S，Suwat K.Adaptive synchronization of hyperchaotic systems via passivity feedback controlwith time-varying gains.Journal of Sound and Vibraion，2010，329（13）：2490～2496

7 张晓芳，陈章耀，毕勤胜.周期激励下Chen系统的簇发现象分析.物理学报，2010，59（6）：3802～3808（Zhang X F，Chen Z Y，BiQ S.Analysis of bursting phenomenon in Chen′s system with periodic excitation.Acta Physica Sinica-Chinese Edition，2010，3802～2808（in Chinese））

8 Bi Qinsheng.The mechanism of bursting phenomenon in BZ chemical reaction with multiple time scales.Science in China Series E，2012，10（3）：2820～2830

9 Gyorgyi L，Field R.A three-variablemodel of deterministicchaos in the Belousov-Zhabotinsky reaction.Nature，1992，355（27）：808～810

10 Valorani M，Goussis D A.Explicit time-scales splitting for stiff problems：auto-lgnition of gaseous-mixtures behind a steady shock.Journal of Computational Physics，2001，169（1）：44～79

11 Rinzel J.Ordinary and Partial Differential Equations.Berlin：Springer-Verlag，1985

12 Simo H，Woafo P.Bursting oscillations in electromechanical systems.Mechanics Research Communications，2011，38（8）：537～541

13 Bertram R，Butte M J，Kiemel T，et al.Topological and phenomenological classification of bursting oscillationa.Bulletin of Mathematical Biology，1995，57（57）：413～439

14 Izhikevich EM.Neural excitability，spiking and bursting.International Journal of Bifurcation and Chaos，2000，10（6）：1171～1266

15 BiQ S，Zhang R，Zhang Z D.Bifurcation mechanism of bursting oscillations in parametrically excited dynamical system.Applied Mathematics and Computation，2014，243（1）：482～491

16 Kitio Kwuimya CA，Enjieu Kadjib H G.Recurrence analysis and synchronization of oscillators with coexisting Attractors.Physics Letters A，2014，387（30-31）：2142～2150

17 Zhang Y X，Kong GQ，Yu JN.Critical curves and coexisting attractors in a quasiperiodically forced delayed system.Physics Letters A，2009，373（15）：1341～1345

18 张晓芳，陈小可，毕勤胜.多分界面下四维蔡氏电路的张弛簇发及其机制研究.物理学报，2013，61（1）：0105021～0105028（Zhang Xiaofang，Chen Xiaoke，Bi Qinsheng.Relaxation bursting and themechanism of fourdimensional Chua′s circuit with multiple interfaces.Acta Physica Sinica-Chinese Edition，2013，61（1）：0105021～0105028（in Chinese））

19 Abooee A，Yaghini-Bonabi H A，Jahed-Motlagh M R.A-nalysis and circuitry realization of a novel three-dimensional chaotic system.Communication in Nonlinear Science＆Numerical Simulation，2013，18（5）：1235～1245

BURSTING COEXISTENCE PHENOMENONOF A FOUR-DIMENSIONAL NON-AUTONOMOUS SYSTEM UNDER PERIODIC EXCITATION*

Zhang Xiaofang†Wu Lei Bi Qinsheng
（Faculty of Civil Engineering and Mechanics，Jiangsu University，Zhenjiang212013，China）

For a periodically excited four-dimensional non-autonomous system，when the exciting frequency is much less than its nature frequency，dynamical behaviors associated with two time scales can be observed.The excited system can be transformed into a general autonomous system by defining thewhole exciting term as a slowvarying parameter.Firstly，the stability and bifurcation conditions of equilibrium points in the generalized autonomous system are presented.Secondly，the slow-fast analysis and transformed phase are employed to explore the different types of bursting behaviors with different initial conditions.In addition，the mechanism of coexistence phenomenon is discussed.Meanwhile，delay phenomenon is observed between the points connecting the spiking states and the quiescent states and the bifurcation points obtained theoretically.

periodic excitation， bifurcation， bursting， two time scales

10.6052／1672-6553-2015-68

2015-10-13收到第1稿，2015-10-23收到修改稿.

*国家自然科学基金资助项目（21276115，11572141）

†通讯作者E-mail：xfzhang＠ujs.edu.cn

Received 13 October 2015，revised 23 October 2015.

*The project supported by the National Natural Science Foundation（21276115，11572141）

†Corresponding author E-mail：fzhang＠ujs.edu.cn