Jacobi椭圆函数展开法在两个非线性偏微分方程解中的应用

阮传同，张瑞丽



Jacobi椭圆函数展开法在两个非线性偏微分方程解中的应用

*阮传同，张瑞丽

（周口师范学院数学系，河南，周口 466001）

介绍构造非线性方程精确解的一种直解代数方法——Jacobi椭圆函数展开法，并分析了Jacobi椭圆函数展开法的适用条件，揭示了Jacobi椭圆函数展开法的解题思想和技巧。最后，运用此方法构造出了两个非线性方程的精确解，并给出特殊情况下的波形图。

Jacobi椭圆函数；秩；非线性方程；齐次平衡法；精确解

自然学科中的很多现象是非线性学科研究的重要内容，我们可以把非线性的许多问题归结为求解非线性偏微分方程的精确解的问题。可由于非线性方程的复杂性，对于非线性方程还没有通用的解法。不过经过长时间不断努力，学者们发现了很多求解非线性演化方程的方法，如齐次平衡法[1]、Jacobi椭圆函数展开法[2]、双曲正切函数展开法[3]、试探方程法[4]等，它们各具特色。其中刘式适提出的Jacobi椭圆函数展开法，不但算法直接，而且求得的非线性偏微分方程的精确解类型丰富，深受学者们喜爱。

本文利用文献[5]提出了“秩”的概念，分析了Jacobi椭圆函数法的适用条件，介绍了Jacobi椭圆函数展开法的基本思想。通过求解两个非线性方程的精确解，加深了对Jacobi椭圆函数展开法的理解。同时，也丰富了非线性方程的精确解。

１ Jacobi椭圆函数展开法[6]

假设非线性方程的一般形式为：

寻找它如下形式的行波解：

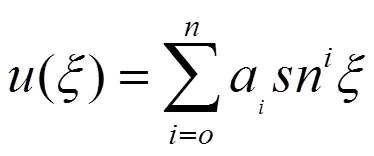
由于

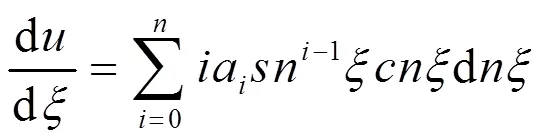
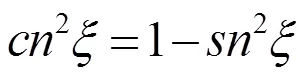
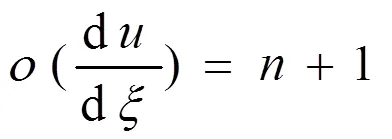
以此类推：

在（3）中选择，使得非线性方程(1)中的非线性项和最高阶导数项平衡。

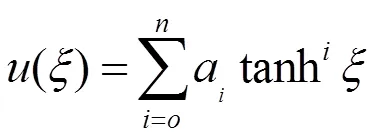
所以Jacobi椭圆函数法包含了双曲正切函数展开法。

下面，对Jacobi椭圆函数展开法适用条件进行分析，把(2)式代入方程(1)，方程可化为

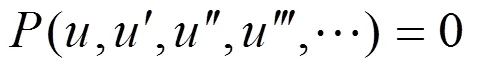
假设方程的项数为，最高阶导数的阶数为，则上式（5）的任一项都可表示为：

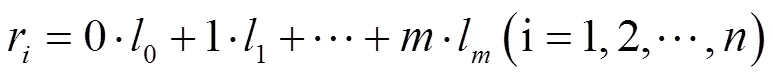
根据Jacobi椭圆函数间的关系，只有(5)中每一项的秩同为奇数或偶数的情况下，才能应用Jacobi椭圆函数展开法来求解方程(1)。

2 求解非线性方程

2.1 非线性波动方程[7]

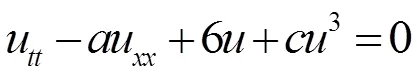
寻找方程行波解：

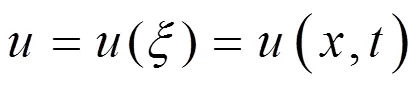
把它代入方程(6)得到常微分方程如下：

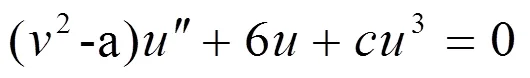
并且

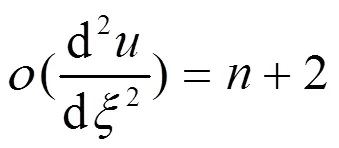
根据齐次平衡原则，应有

从而，得到=1。

因此方程有如下形式的解：

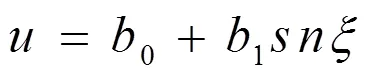
对其求二阶导，得

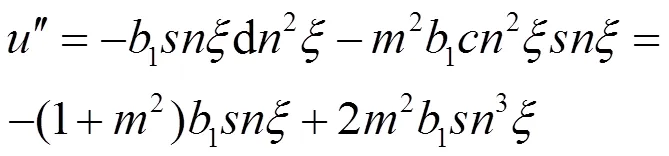
把（8）、（9）代入（7），得

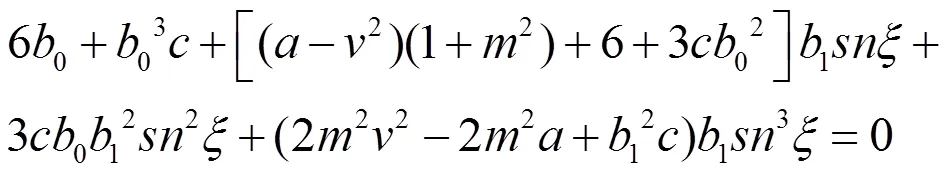
根据吴消元法得到

从而，得到方程（6）的精确解为：

2.2 Zhiber-Shabat方程[8]

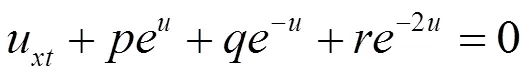
首先作变换

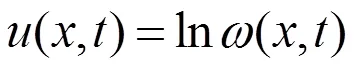
将（11）代入方程（10），可得

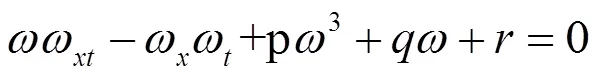
再作行波变换

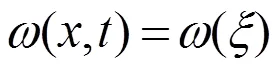
其中为待定非零常数，将(13)代入方程(12)得

并且

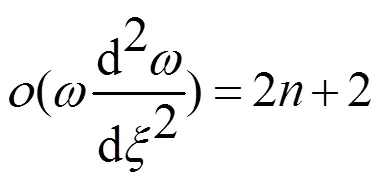
根据齐次平衡原则

对其求导得

并且

把（15）、（16）、（17）、（18）代入（14）得方程

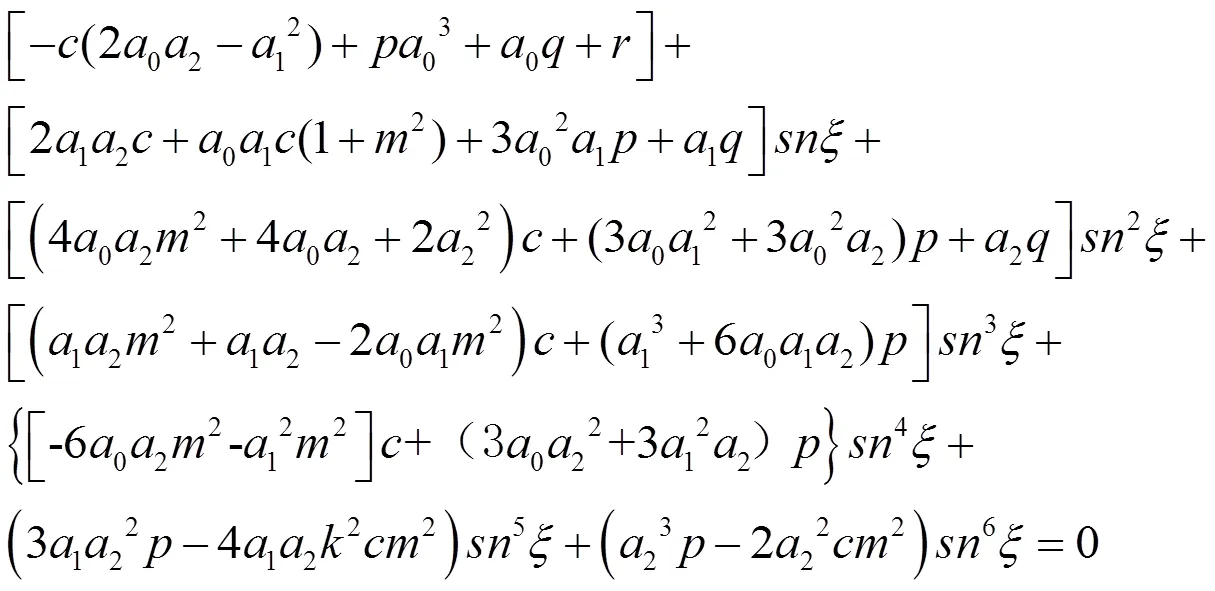
根据吴消元法得到

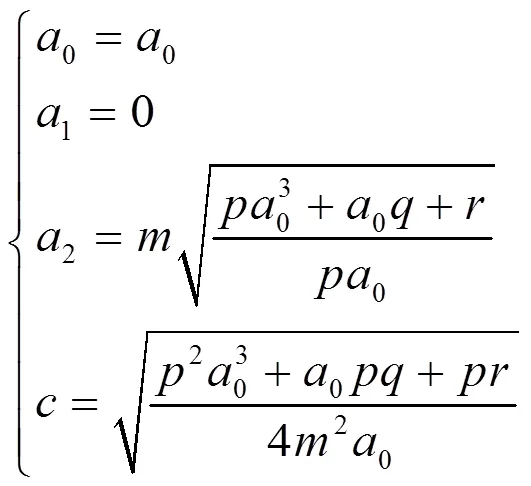
将（20）代入（15），则

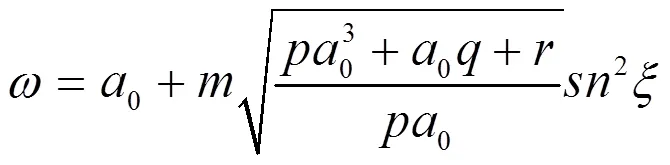
最后将(13)，(22)代入(11)中可得到方程(10)的精确解为：

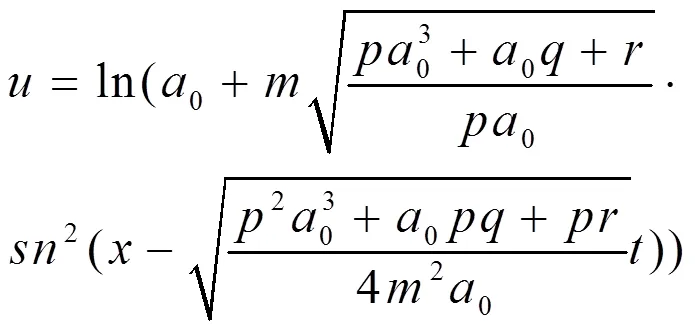
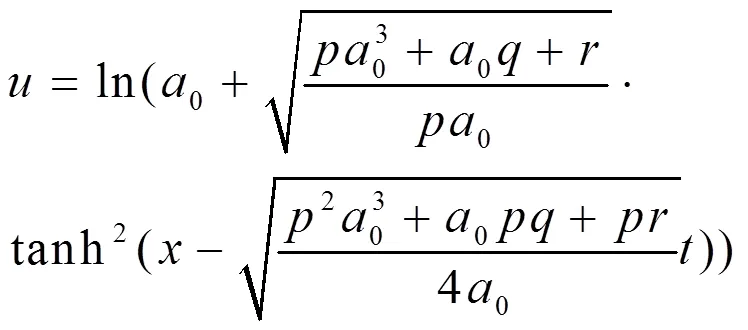
这时，（24）、（26）可约化为

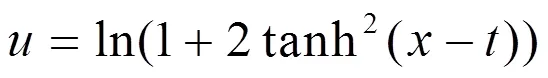
３　总结

把自然学科中的非线性问题化为非线性偏微分方程求解，具有很重要的意义。通过介绍Jacobi椭圆函数展开法，求解了两个非线性偏微分方程的显式精确解，清楚了此方法的解题思路和步骤。仿照此方法，利用换算关系，同样可以求解出其它形式的Jacobi椭圆函数解，限于篇幅，本文从略。值得注意的是，一定要在Jacobi椭圆函数展开法适用的条件下才能使用此方法。Jacobi椭圆函数展开法在很多自然科学中求解其它重要的方程也发挥着重要的作用。

[1] 范恩贵，张鸿庆. 非线性孤子方程的齐次平衡法[J].物理学报,1998,47 (3):353-362.

[2] 刘式适.Jacobi椭圆函数展开法及其在求解非线性波动方程中的应用[J].物理学报,2001,50(11):2068-2073.

[3] Parkes E J, Duffy B R.Travelling solitary wave solutions to a compound KdV-Burgers equation[J].Physics Letters A,1997,229:217-220.

[4] 刘成仕.试探方程法及其在非线性发展方程中的应用[J]. 物理学报,2005,54 (6) :2505-2509.

[5] 张善卿, 李志斌. Jacobi 椭圆函数展开法的新应用[J]. 物理学报, 2003, 52(5):1066-1069.

[6] 沈水金.Jacobi椭圆函数展开法的应用[J].绍兴文理学院学报,2006,26(10):13-16.

[7] 曹瑞.一类非线性波动方程的精确行波解[J].大学物理，2012,31(6):25-27.

[8] 郭鹏，张磊，王小云，等.几个特殊类型非线性方程的显示精确解[J].山东大学学报: 理学版, 2012,47(12): 117-120.

Jacobi elliptic function expansion method is applied to two nonlinear partial differential equations

*RUAN Chuan-tong, ZJANG Rui-li

(Department of Mathematics, Zhoukou Normal University, Zhoukou, Henan 466001, China)

We mainly introduced a method of direct Algebra -- the Jacobian elliptic function expansion method, using for constructing the exact solutions to the nonlinear equations. We also analyzed the application conditions of the Jacobi elliptic function expansion method. Furthermore, we revealed the solving ideas and skills of the Jacobi elliptic function method. Finally, we constructed the exact solutions of two nonlinear equations based on the method and the waveform diagram was given under special circumstances.

Jacobi elliptic function expansion method; rank; nonlinear equation; homogeneous balance method; exact solution

1674-8085(2013)05-0004-05

O159.1

A

10.3969/j.issn.1674-8085.2013.05.002

2013-05-08；

2013-07-16

周口师范学院青年科研基金项目(2012QNB09)

*阮传同(1979-)，男，河南淮阳人，讲师，硕士生，主要从事孤立子与可积系统研究(E-mail:ruangong8888@sina.com);

张瑞丽(1989-)，女，河南中牟人，主要从事偏微分方程及应用研究(E-mail:859142354@qq.com).