二阶非线性动力方程有界解振动的充分必要条件

王志伟，邓志云，杨云苏



二阶非线性动力方程有界解振动的充分必要条件

*王志伟，邓志云，杨云苏

（井冈山大学数理学院，江西，吉安 343009）

利用Lebesgue控制收敛定理，给出了二阶非线性动力方程有界解振动的充分和必要条件。

二阶动力方程；振动性；时标

0 引言

随着微分方程和差分方程的研究逐渐深入，人们发现微分方程的很多结果可以直接应用到差分方程上去。但在某些结论上，他们又有着本质的不同。这时人们把目光放在这个问题上，能不能找到一个新的东西，能够将二者统一起来。1988年Stefan Hilger 首先提出了时标的概念，它将连续分析和离散分析两种理论统一起来。实际生活中有许多时标的例子。例如，一年生植物的繁殖模型，假设该植物的数量在某一季节是连续的，而在冬季会全部死亡，但是他们的种子又会在新的季节生根发芽，成为不交叉的种群数量。泛函微分方程的振动性理论和差分方程的振动理论是方程定性理论的两个重要分支，如文献[2]-[7]，而时标上动力方程作为方程的一个新领域，其振动性理论近年来更是引起国内外学者的关注，如文献[8-10]，他们研究了几类的动力方程的振动性问题。

本文讨论二阶非线性动力方程

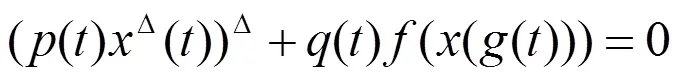
在文中假设：

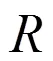
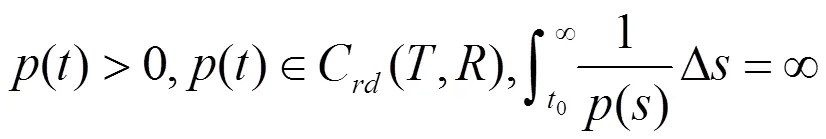
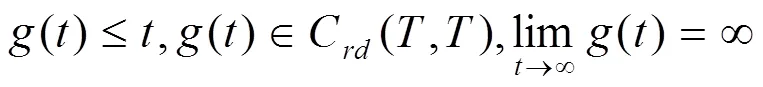
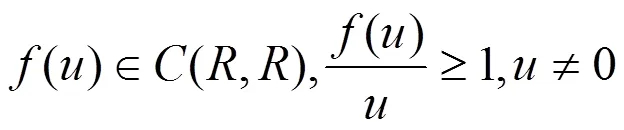
1 预备知识

定义1.1[1]设为实数集的任意非空闭子集，则称为一时标。例如实数集，整数集，自然数集都是时标；但有理数集，无理数集，复数集，开区间(1，2)都不是时标。

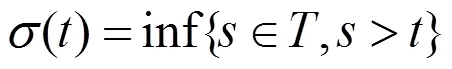
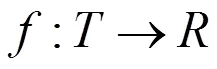
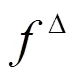
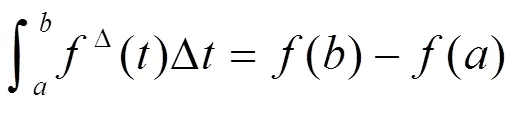
2 主要结果

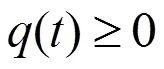
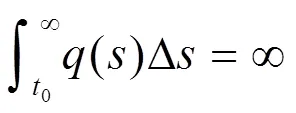
则方程(0.1)是振动的。

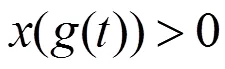
由方程(0.1)及条件(4)有

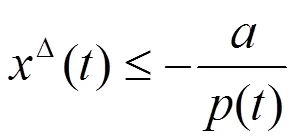
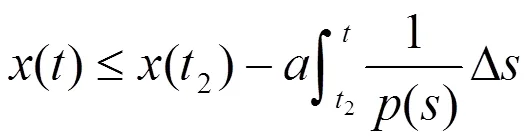
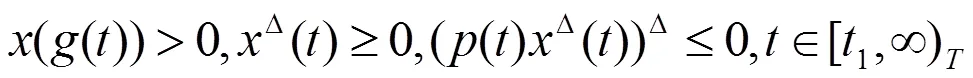
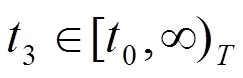
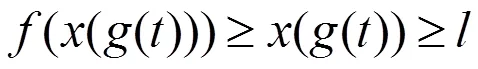
将(2.5)代入(0.1)，得到

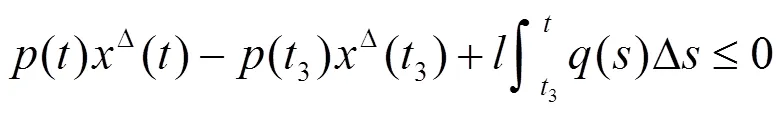
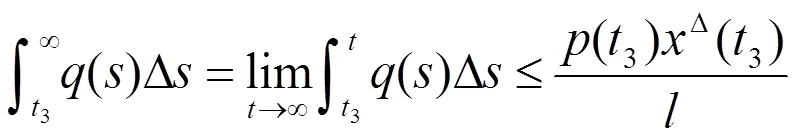
与假设条件(2.1)矛盾。证毕。

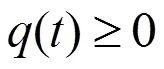
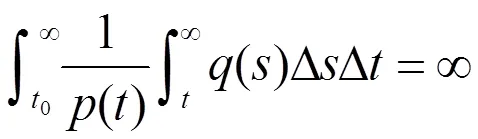
证明：充分性

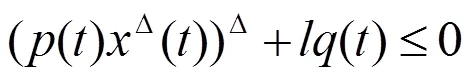
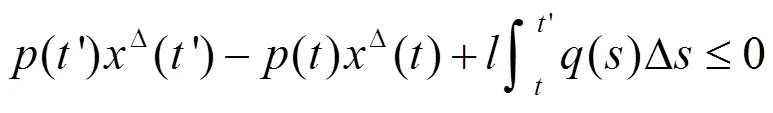
必要性

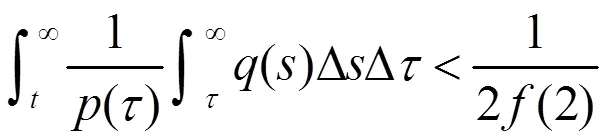
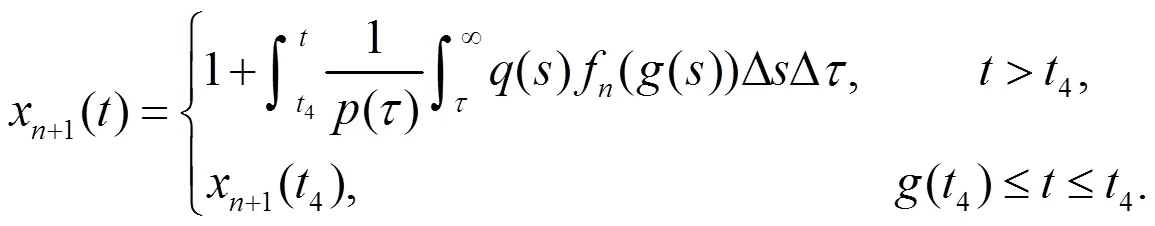
则有

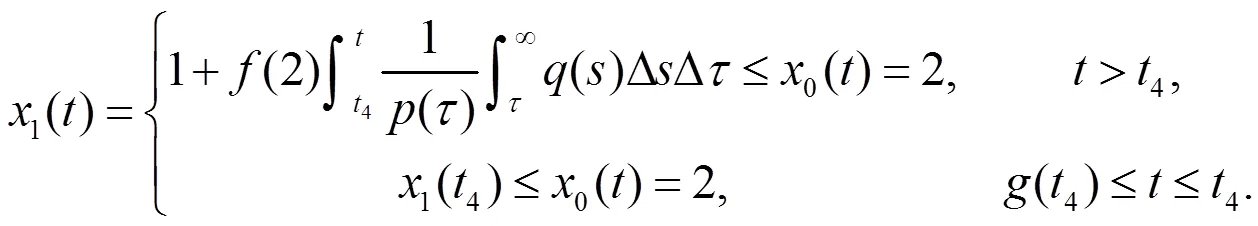
由数学归纳法知：对任意正整数，则有

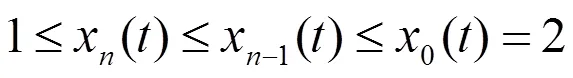
3 例题

考虑二阶非线性动力方程

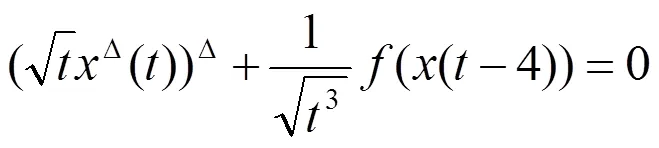
从而得

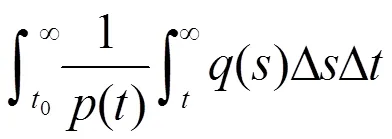
利用定理2.2知，方程（3.1）的每一个有界解都是振动的。

[1] Bohner M, Peterson A. Dynamic Equations on Time Scales[M]. Boston: Birkhauser, 2001.

[2] Ebe L H, Kong Q K, Zhang B G. Oscillation theory for functional differential equations[M]. New York: Marrcel Kekker, 1995.

[3] Yang Jun, Wang Chunyan, Guan Xinping. Oscillation of a nonlinear variable delays difference equation with nonlinear neutral terms[J]. Pure and Applied Mathematics, 2005,21: 300-304.

[4] 林丹玲.非线性中立型微分方程的振动准则[J]. 西南师范大学学报:自然科学版, 2008, 33(1): 22-26.

[5] 韩振来,孙书荣.带有多个变滞量的二阶中立型差分方程振动性判据[J].数学实践与认识, 2002,32(1):61-64.

[6] 欧阳瑞,陈春华.二阶中立型时滞差分方程的振动性与正解存在性[J].四川理工学院学报,2011,24（2）:145-147.

[7] 杨甲山. 具有正负系数的二阶非线性中立型差分方程正解的存在性[J]. 邵阳学院学报, 2010,7(1):1-5.

[8] Zhang B G, Zhu S. Oscillation of Second Order Nonlinear Dynamic Equations on Time Scales [J]. Computers Math Applic, 2005,49(4):599-609.

[9] Bohner M, Saker S H . Oscillation of Second-Order Nonlinear Dynamic Equations on Time Scales [J]. Rocky Mountain J Math, 2004,34(4):1239-1254.

[10] Erbe L, Peterson A,Saker S H. Oscillation Criteria for Second Order Nonlinear Dynamic Equations on Time Scales [J]. Math Anal Applic, 2007,333:505-522.

Necessary and Sufficient Conditions for Oscilation of Bounded Solutions of Second order Nonlinear Dynamic Equations

*WANG Zhi-wei，DENG Zhi-yun，YANG Yun-su

(School of Mathematics and physics jinggangshan University, Ji’an, Jiangxi 343009, China )

We mainly give necessary and sufficient conditions for oscilation of bounded solutions of second order nonlinear dynamic equations by Lebesgue’s Dominated Convergence Theorem.

second order dynamic equation; oscillation; time scales

1674-8085(2013)05-0009-04

0175.1

A

10.3969/j.issn.1674-8085.2013.05.003

2013-04-08；

2013-05-21

*王志伟(1977-)，男，江西吉水人，讲师，硕士，主要从事动力系统与稳定性研究(E-mail:whzhwh_2003@126.com);

邓志云(1975-)，男，江西吉水人，副教授，硕士，主要从事应用数学研究(E-mail:danzhiyun@163.com);

杨云苏(1968-)，女，江西泰和人，副教授，硕士，主要从事泛函分析研究(E-mail:pengyou19820124@163.com).