Local Existence and Global Nonexistence Theorems for a Viscous Damped Quasi-Linear Wave Equations

SONG Ruili(宋瑞丽),WANG Shubin(王书彬)

( 1.College of Information and Business,Zhongyuan University of Technology,Zhengzhou 450007,China; 2.School of Mathematics and Statistics,Zhengzhou University,Zhengzhou 450001,China)

Abstract: In this paper,the existence and uniqueness of the local solution for the initial boundary value problem for a class of three-dimensional space of quasi-linear viscous damping wave equation are proved by the Galerkin method and compactness principle.The blow-up of the solution in limited time for this question is proved by means of the energy integral inequality.

Key words: Viscous damped; Quasi-linear wave equation; Initial boundary problem;Local solution; Blow-up of solution

1.Introduction

In this paper,we consider the 3-dimensional initial boundary value problem:

whereu(x,t)denotes the unknown function,α>0,β >0,p ≥1,q >1 are constants,f(s)is a given nonlinear function,the subscripttindicates the partial derivative with respect tot,∇denotes the gradient operator,u0andu1are the given initial value function,Ωis a bounded domain in R3with a smooth boundary∂Ω.

The equations of the type of(1.1)are a class of nonlinear development equations which are proposed to control the motion of a viscoelastic solid of the material of the rate type.[1−3,5−6]It can also be considered as the longitudinal field equation governing the viscoelastic bar obeying the nonlinear Voigt model.[4]Whenα=β=0,there have been a lot of results on the global existence and other natures of solutions of the equation(1.1).[1−2,7,10]In[8],YANG and CHEN have proved the global existence and uniqueness of the solution of (1.1)-(1.3)in one-dimensional space when the authors replacedα|ut|p−1utandβ|u|q−1ubyf(ut)andg(u).In [9],the authors have proved the existence and uniqueness of the local generalized solution and the local classical solution and given the conditions for blow-up of the solutions in finite time,but they were all in one-dimensional space.In the present paper,we overcame the design problem of embedding theorem and interpolation theorem index and proved the existence and uniqueness of the local solution of (1.1)-(1.3)under certain conditions in three-dimensional space.

Throughout this paper,we use the notation:||·||p=||·||Lp(Ω)(1≤p ≤∞),||·||m(Ω)=||·||Hm(Ω),||·||Wm,p=||·||Wm,p(Ω).In particular,||·||=||·||2.Ci(i=1,2,···)are positive constants,and they don’t depend onNandt.

2.The Existence and Uniqueness of Local Solution

In this section we will prove the existence and uniqueness of local solution for the problem(1.1)-(1.3)by the Galerkin method and compactness principle.

Let{yi(x)} be the orthonormal basis inL2(Ω),namely∇2y+λy=0.

Let

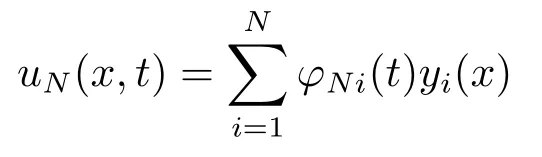
be the Galerkin approximate solutions of the problem (1.1)-(1.3),whereφNi(t)are the undermined functions,Nis a natural number.Suppose that the initial value functionu0andu1can be expressed as

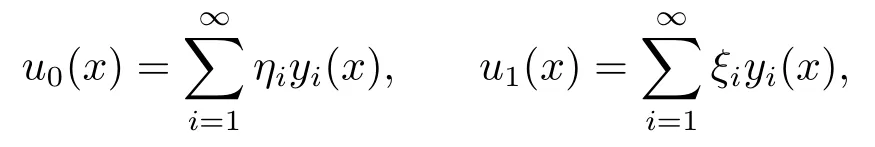
whereηiandξiare constants,uN(x,t)is determined by the following system of ordinary differential equations

Lemma 2.1Suppose thatf ∈C3(R),|f(s)|≤K|s|ν,|f′(s)|≤K|s|ν−1etc.,andf′′(0)=0,whereν ≥2 is natural number,K >0 is constant,q >1,p ≥1 and min {p+1,q+1}≥3.If

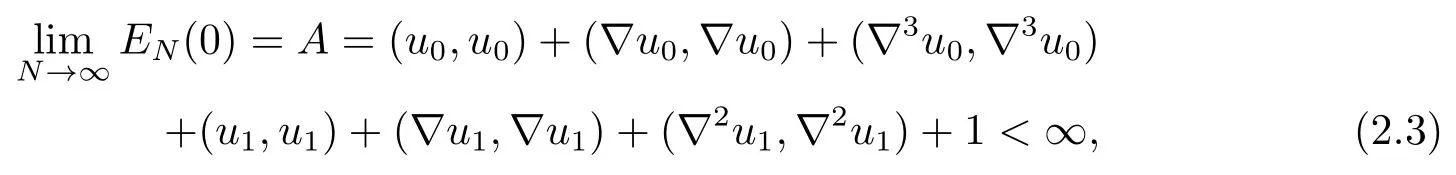
then the initial value problem (2.1)-(2.2)admits the classical solutionφ(t)=(φN1(t),φN2(t),··· ,φNN(t))on [0,t1]and

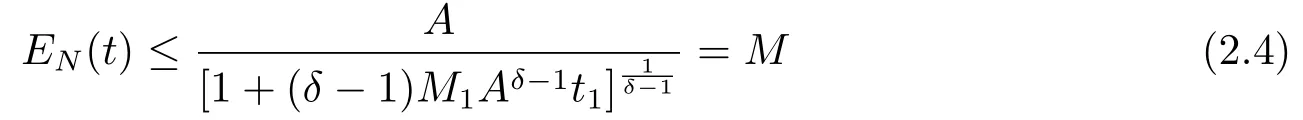
is uniformly bounded,wheret1,M1are positive constants independent of the boundM,and

ProofThe local solution of the initial value problem(2.1)-(2.2)always exists according to ordinary differential equation theory.Let [0,TN]be the maximum time interval in which the solution exists.Now we are going to estimate the solution of the initial value problem(2.1)-(2.2).

Multiplying both sides of the equation (2.1)by 2(1+λs+λ2s)(t)and summing up fors=1,2,··· ,N,adding 2[(uN,uNt)−(∇2uN,uNt)+(∇3uN,∇3uNt)]to both sides of(2.1)and integrating by parts ofx,we have

Using the Gagliardo-Nirenberg interpolation theorem and (2.5),we can get

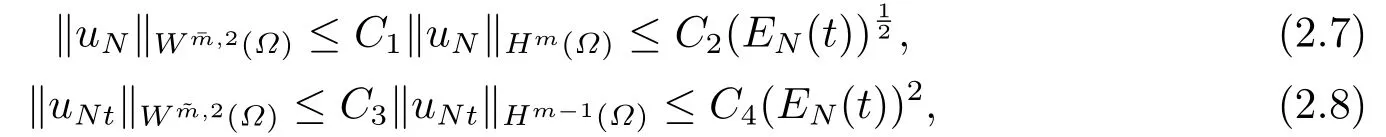
where 0≤≤m−1≤4,0≤≤m−2≤3.Using the Hlder inequality,(2.7),(2.8)and the assumption of Lemma 2.1,we obtain

By using of the differentiation and the assumptions off(s),we have calculation that

Making use of the Hölder inequality,the Cauchy inequality,from (2.5)and (2.11),we obtain that

Using differential method and simple calculation,we arrive at

We obtain from (2.11),(2.13)and (2.14)that

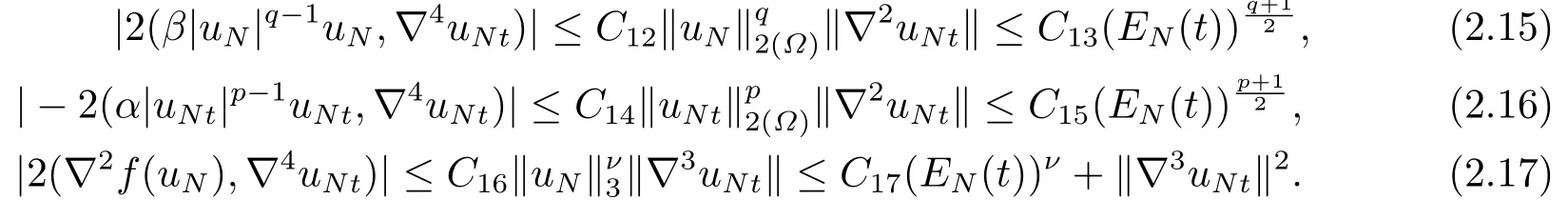
From (2.5)and the Hölder inequality,we conclude that

Substituting (2.9)(2.10)(2.12)and (2.15)-(2.18)into (2.6),we get

whereM1>0 is a constant independent ofN,for anyt ∈(0,TN).It follows from (2.19)that

If we take the appropriatet1to make 0<1+(1−δ)M1t1Aδ−1< ηtrue,where 0< η <1,then (2.4)holds on [0,t1].This means thatTNhas the positive lower bound independent ofN.Lemma 2.1 is proved.

It is easy to deduce the following lemma is true from Lemma 2.1

Lemma 2.2Under the conditions of Lemma 2.1,the approximate solutionuNof the question (1.1)-(1.3)has estimation as follows

Theorem 2.1Suppose thatf ∈C3(R),|f(s)|≤K|s|ν,|f′(s)|≤K|s|ν−1etc.,andf′′(0)=0,whereν ≥2 is natural numbers,K >0 is constant,q >1,p ≥1 and min {p+1,p+1}≥3.Ifu0∈H2(Ω),u1∈H2(Ω),then the initial boundary value problem (1.1)-(1.3)has a unique local generalized soluteu(x,t).

ProofMultiplying both sides of the equation (2.1)by 2äN,sand summing up fors=1,2,··· ,N,we arrive at

Using the Hölder inequality and the Cauchy inequality,using (2.11)(2.13)(2.14)(2.21)and(2.22),we obtain

Using the Sobolev imbedding theorem and (2.21),we obtain

where 0< λ ≤0.5.It follows from (2.24)and the Ascoli-Arzel´a theorem that there exists a functionu(x,t)and a subsequence of{uN(x,t)},still labeled by{uN(x,t)},such that whenN→∞,{∇iuN(x,t)}(i=0,1,2)and{uNt(x,t)} uniformly converge to∇iu(x,t)(i=0,1,2)andut(x,t)on,respectively.The subsequence{∇iut(x,t)}(i=1,2)weakly converge to∇iut(x,t)(i=1,2)inL(Qt1).Thus the initial boundary value problem (1.1)-(1.3)has a local generalized solution.

We now demonstrate the uniqueness of local generalised solutions.Suppose thatu(x,t)andv(x,t)are two generalized solutions of the initial boundary value problem(1.1)-(1.3).Let

Thenω(x,t)satisfies the initial boundary value problem

Multiplying both sides of equation (2.25)by−2∇2ωt,increasing 2ωωt−2∇4ωωtto the both sides and integrating onΩ,using the Cauchy inequality,we arrive at

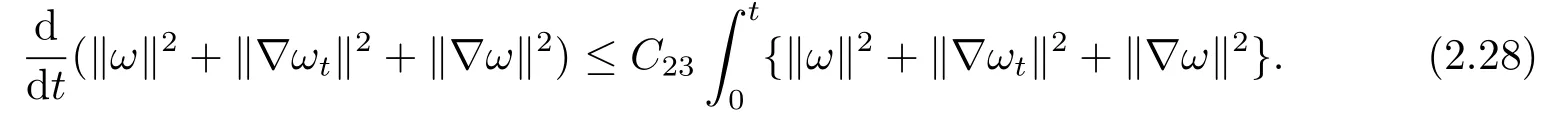
The Gronwall inequality yields

Thereforeu(x,t)=v(x,t).This completes the proof of the theorem.

To prove the local classical solution of the question (1.1)-(1.3),we estimate the approximate solution furtherly.

Lemma 2.3Suppose that the conditions of Lemma 2.2 hold,andf ∈C7(R),f(2l−1)(0)=0,l=1,2,3,4,u0∈H7(Ω),u1∈H6(Ω),then the approximate solution of the problem (1.1)-(1.3)has the following estimates

ProofMultiplying both sides of equation(2.1)by 2(1+λ6s)(t)and summing up fors=1,2,··· ,N,adding 2[(uN,uNt)+(∇2uN,∇12uNt)]to both sides of (2.1)and integrating by parts ofx,we obtain that

where

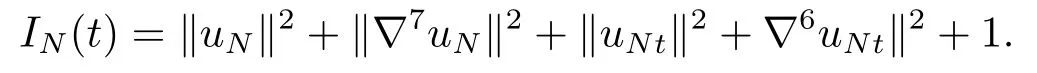
Making use of the Hölder inequality,the Cauchy inequality,analogous to (2.9)(2.10),we get

By virtue of the Hölder inequality,the Cauchy inequality and (2.30),we have

Substituting (2.31)-(2.34)into (2.30),we infer

Multiplying both sides of the equation (2.1)by(t)and summing up fors=1,2,··· ,N,making use of Hölder inequality and Cauchy inequality,similarly to(2.31)-(2.33),we conclude that

Differentiating(2.1)with respect tot,multiplying both sides byλ2s...αN,s(t)and summing up fors=1,2,··· ,N,we can find

By means of Cauchy inequality and Hölder inequality,from (2.37)we arrive at

It is easy to see that (2.29)is valid from (2.35)(2.36)(2.38).This completes the proof of the lemma.

Theorem 2.2Suppose thatf ∈C7(R),|f(s)|≤K|s|ν,|f′(s)|≤K|s|ν−1etc.,f2l(0)=0,l=1,2,3,4,whereν ≥2 is natural numbers,K >0 is constant,q >1,p ≥1 andmin{p+1,p+1} ≥3.Ifu0∈H7(Ω),u1∈H6(Ω),then the initial boundary value problem(1.1)-(1.3)has a unique local classical solutionu(x,t).

ProofIt follows from (2.29)and Sobolev embedding theorem that

where 0< λ ≤0.5.It follows from (2.24)and the Ascoli-Arzel´a theorem that the initial boundary value problem (1.1)-(1.3)has local classical solutionu(x,t).It is easy to see the classical solution of the initial boundary value problem (1.1)-(1.3)is unique.This completes the proof of the theorem.

3.The Global Nonexistence Theorem of the Solution

In this section,to acquire the global nonexistence theorem of the solution for the initial boundary value problem (1.1)-(1.3),we quote the following lemma.

Lemma 3.1[9]Suppose that a positive differentiable functionM(t)satisfies the inequality

with

whereM(0),˙M(0),r >1,C >0 are constants and

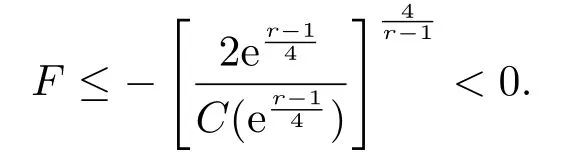
Then there is a constant ˜Tsuch thatI(t)→∞ast→.

Theorem 3.1Suppose thatp=1,q >1,u0∈H10(Ω)∩Lq+1(Ω),u1∈H10(Ω),f(s)∈C1(Ω),sf(s)≤KG(s),G(s)≤−η|s|r+1,G(∇u0)∈L1(Ω)and

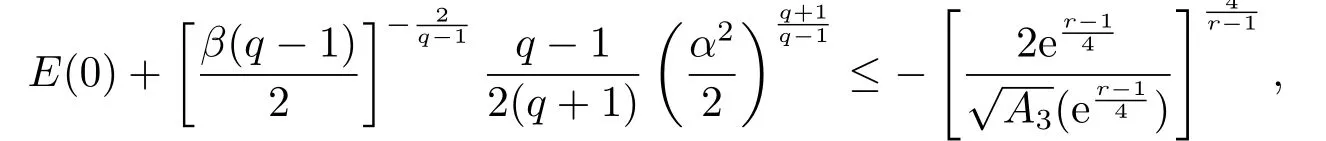
whereG(s)=f(y)dy,K >2,η >0,r >1,

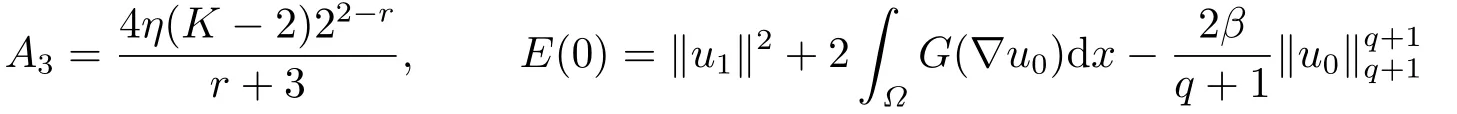
are constants.Then the generalized solution or the classical solution of the initial boundary value problem (1.1)-(1.3)blows-up in finite time,i.e.,

whent→.

ProofAssume that the maximal time of existence of the initial boundary value problem (1.1)-(1.3)is infinite.Multiplying both sides of (1.1)by 2u(t),integrating overΩand integrating by parts,we get(t)=0,t>0,where

ThusE(t)=E(0),t>0.

Let

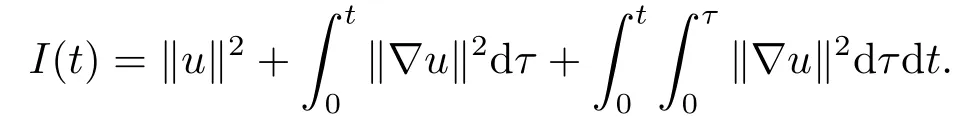
We get

Further we infer by the assumptions of Theorem 3.1 that

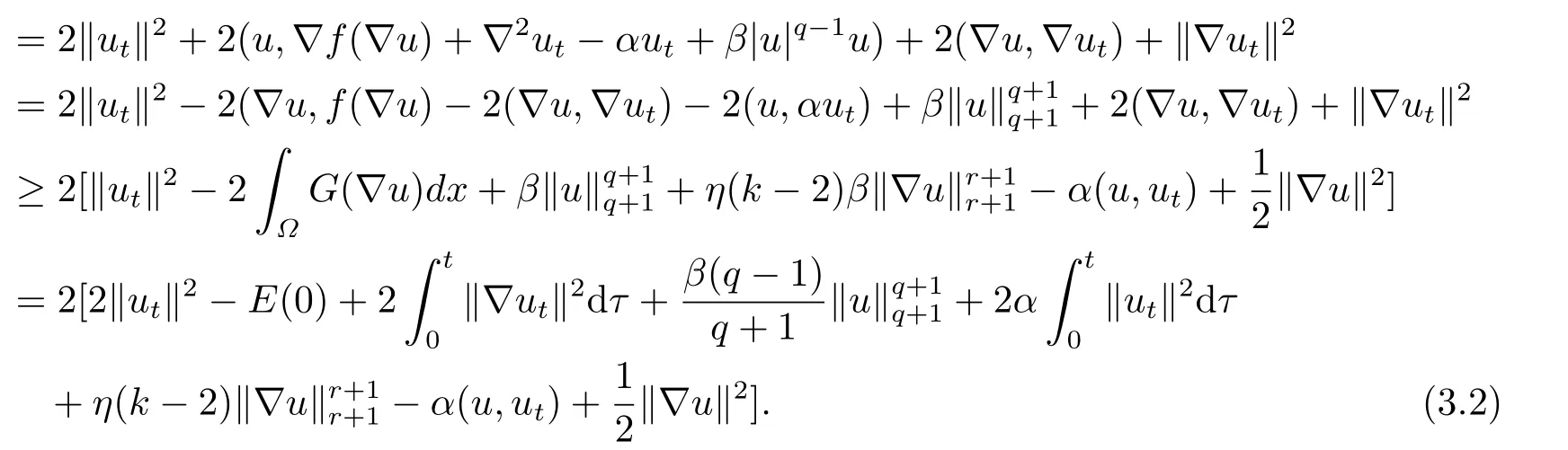
Making use of the Cauchy inequality,the Hölder inequality and the Young inequality,we have

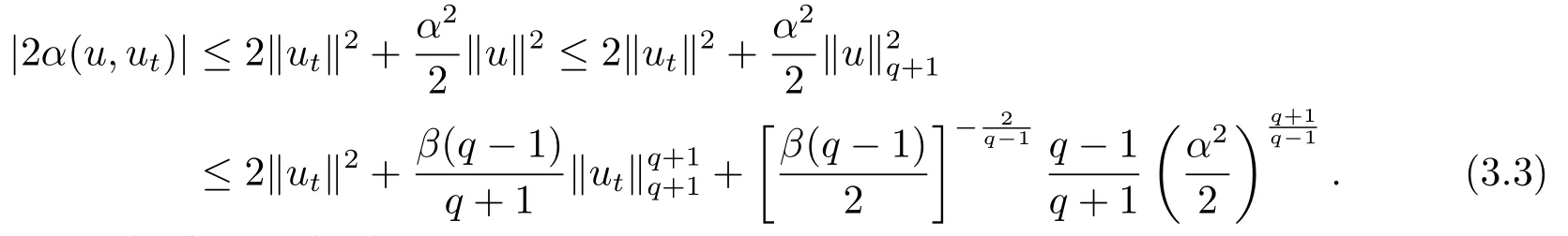
Substituting (3.3)into (3.2),we can find

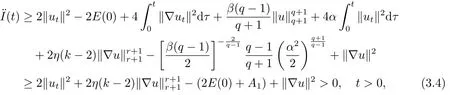
where

It follows from (3.4)that

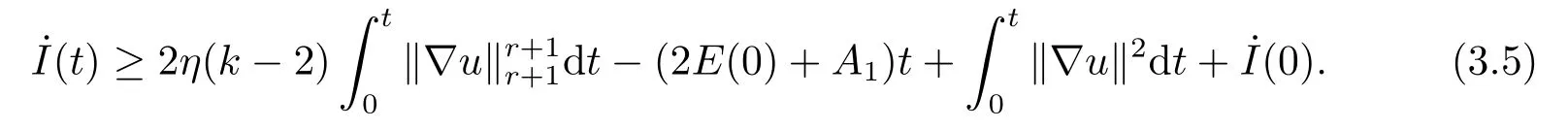
Further

From (3.1)(3.4)-(3.6)and the Cauchy inequality,we obtain

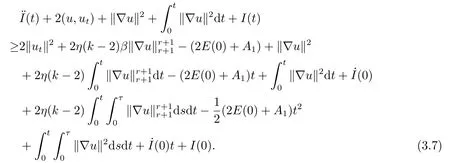
Since 2(u,ut)≤||u||2+||ut||2and>0,I(t)>0,from (3.7)we deduce

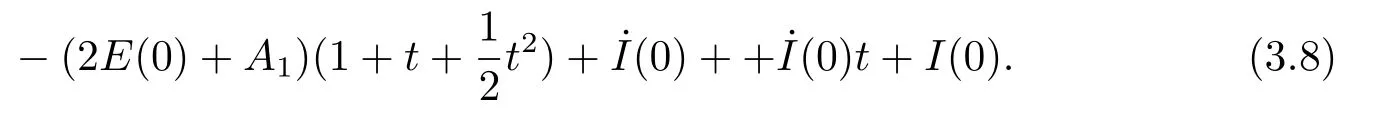
Using the Hölder inequality and the Poincarinequality,we assert

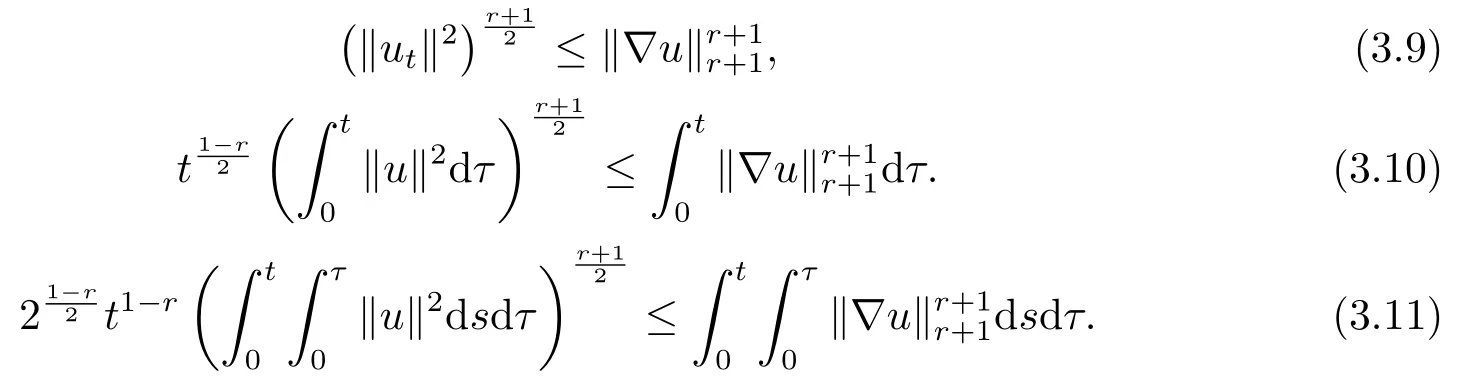
Using the inequality

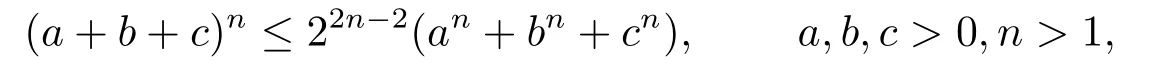
and substituting (3.9)-(3.11)into (3.8),we find

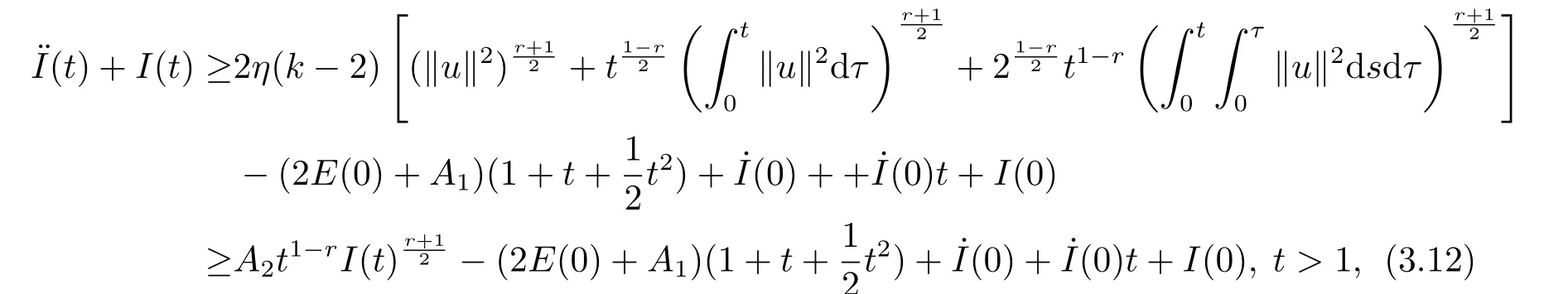
whereA2=η(k−2)22−r.

It follows from (3.5)and (3.6)that ˙I(t)→∞ast→∞.Therefore ,there exist at0≥1 such that ˙I(t)>0,I(t)>0 whent ≥t0.Multiplying both sides of (3.12)by 2 ˙I(t)and using(3.5),we obtain

Integrating (3.13)over (t0,t),we infer that

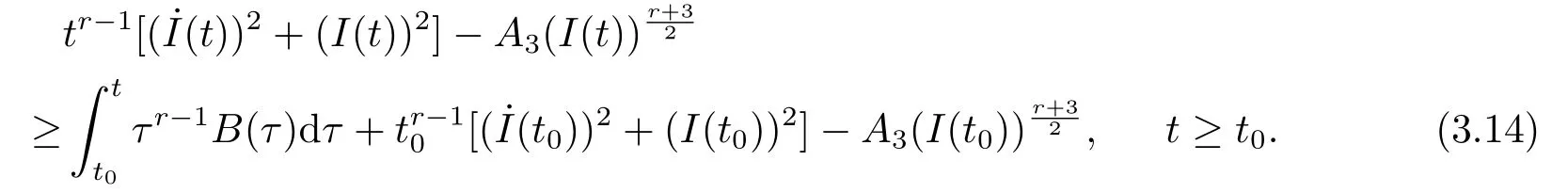
We observe that the right-hand side of(3.14)approach to positive infinity ast→∞,so there is at1≥t0such that the right-hand side of (3.14)is large than or equal to zero whent ≥t1.We thus get

Further from (3.15)we conclude that

By virtue of Lemma 3.2 there exists a constant,such that

ast→.The theorem is proved.

Similarly to Theorem 3.1,we can prove

Theorem 3.2Suppose thatH10(Ω),f(s)∈C1(Ω),sf(s)≤KG(s),G(s)≤−η|s|r+1,G(∇u0)∈L1(Ω)and

where

are constants.Then the generalized solution or the classical solution of the initial boundary value problem (1.1)-(1.3)blows-up in finite time,i.e.,

whent→.