Long-Time Dynamics of Solutions for a Class of Coupling Beam Equations with Nonlinear Boundary Conditions
WANG Yu(王瑜),ZHANG Jianwen(张建文)
( Department of Mathematics,Taiyuan University of Technology,Taiyuan 030024,China)
Abstract: In this paper,we study long-time dynamics of solutions for a class of coupling beam equations with strong dampings under nonlinear boundary conditions.Firstly,we prove the existence and uniqueness of global solutions by some inequalities and prior estimates methods.Secondly,by an absorbing set and asymptotic compactness of the related solution semigroup,we prove the existence of a global attractor.
Key words: Coupling beam equation; Nonlinear boundary condition; Global attractor
1.Introduction
This problem is derived from the equation
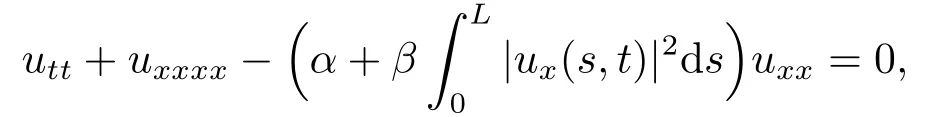
which was proposed by Woinowsky-Krieger[1]as a model for vibrating beams with hinged ends.WANG et al.[2]proved the strong global attractor for the Kirchhoff beam equationssubjected to the boundary conditionsu=uxxon∂Ω×R+.Chueshov[3]studied well-posedness and long time dynastic of a class of quasilinear wave equation with a strong damping.The attractor on extensible beams with null boundary conditions were studied by some authors[4−8].
In the following,we make some comments about previous works for the long-time dynamics of the beam equation with nonlinear boundary conditions.MA[4]studied the existence and decay rates for the solution of the Kirchhoff-type beam equation with non-linear boundary conditions and proved long-time behavior of a model of extensible beam

with the absence of the structural damping and the rotational inertia,subjected to the nonlinear boundary conditions
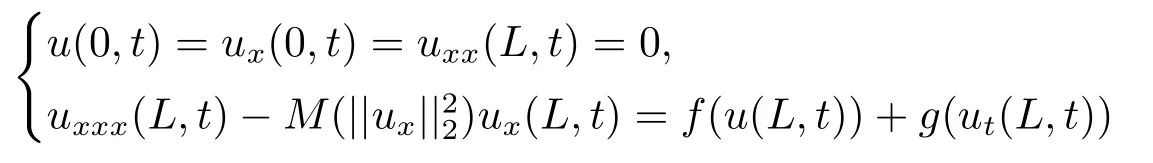
in [9]and [10]respectively.WANG et al.[11]considered a kind of more general nonlinear Kirchhoff-type beam equation
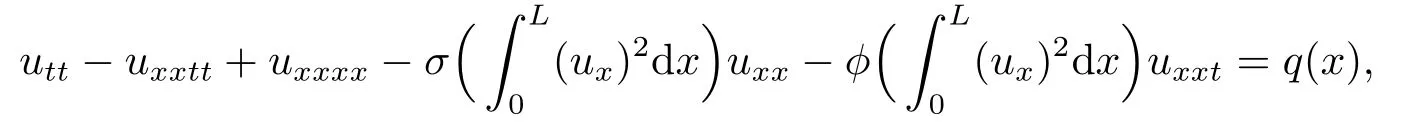
subjected to the nonlinear boundary conditions

In addition,we mentioned some results on solution of coupling equations.Choo and Chung[12]considered the solution of the nonplanar oscillatory beam equations

under planar external force,whereψ(ω1,ω2,ω3)= {β+γ(||ω1||22+||ω2||22)}ω3.
We also mentioned some results on global attractor of coupling beam equations.Giorgi et al.[13]considered a class of thermoelastic coupled beam equations and proved the existence of weak solution and global attractor.However,the long time behavior of the coupling beam equations with nonlinear boundary conditions was paid little attention.
In this paper,we will study the global attractor of coupling beam equations
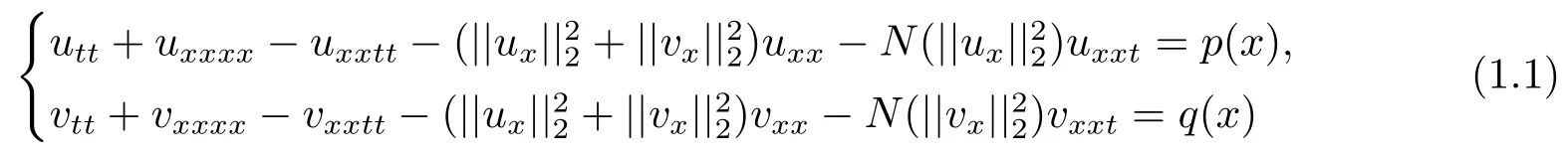
with strong dampings,subjected to the nonlinear boundary conditions
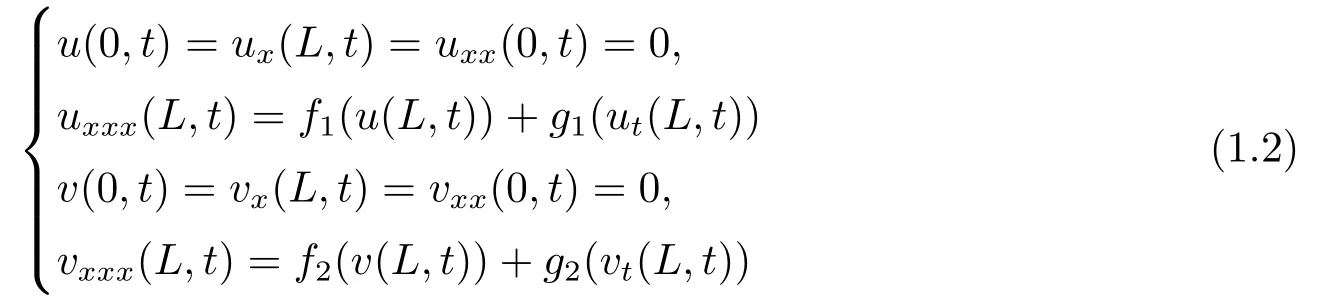
and the initial conditions

HereΩ=(0,L)is a bounded domain of R;N(·)is continuous nonnegative nonlinear real function.−uxxttand−vxxttrepresent the rotational inertias;N(||ux||22)uxxtandN(||vx||22)vxxtexpress the strong dampings;p(x)andq(x)are external force terms.
The paper is organized as follows.In Section 2,we introduce some function assumptions and Sobolev spaces.In Section 3,we prove the existence of global weak and strong solution of coupling beam equations with strong dampings.In Section 4,we discuss the existence of a global attractor of the system (1.1)-(1.3).
2.Some Spaces and Functions Assumptions
Our analysis is based on the following Sobolev spaces.Let

Motivated dy the boundary conditions (1.2)we assume,for regular solutions,that data(u0,u1,v0,v1)satisfies the compatibility conditions
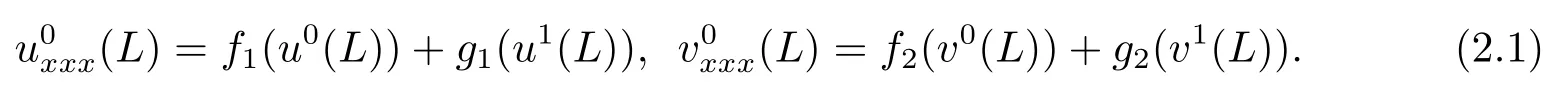
For regular solutions we consider the phase space
H1= {(u0,u1,v0,v1)∈W ×W ×W ×W; satisfies conditions (1.2)}.
For weak solutions we consider the phase spaceH0=V ×U ×V ×U,which guarantees that for regular data,the compatibility conditions(1.2)hold.InH0we adopt the norm defined by
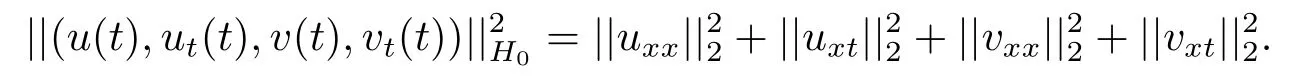
Assumption 1We assume thatfi,gi,i=1,2:R→R are of classC1(R),satisfyfi(0)=gi(0)=0,i=1,2,and there exist constantski,pi,mi >0,L0,Li >0,ρ,r ≥0,∀u,v ∈R

Assumption 2The functionN(·)∈C1(R)is nondecreasing and satisfies

Assumption 3p(x),q(x)∈L2(Ω).
3.The Existence of Global Solution
Theorem 3.1Assume Assumptions 1-3 hold,for any initial data (u0,u1,v0,v1)∈H1,there exists a unique regular solution (u(t),v(t))of the problem (1.1)-(1.3)such that

whereM1>0 only depends on the initial data,pandq.
ProofLet us consider the variational problem associated with(1.1)-(1.3):findu(t),v(t)∈W,∀ω,∈Vsuch that
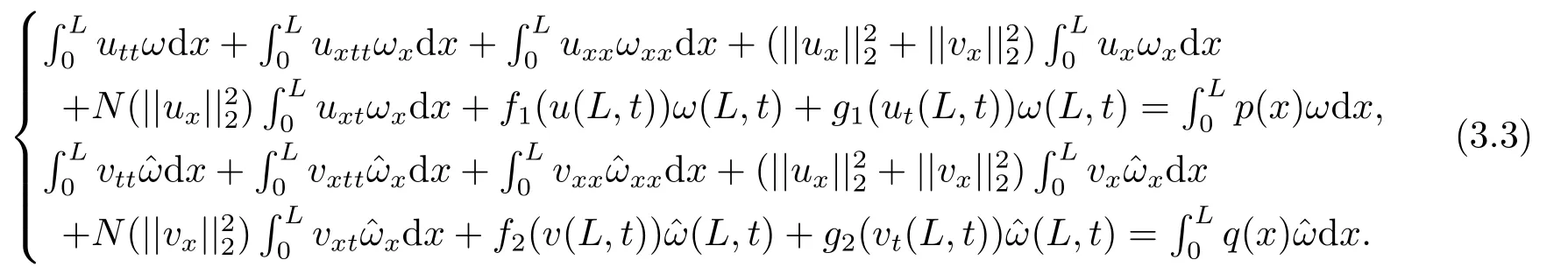
Estimate 1 In the first approximate equation and second approximate equation of(3.3),respectively puttingω=umt(t)and=vmt(t),using the Schwarz inequality,then integrating from 0 tot Taking into account the assumption (3.4),andN(·),,,we see that there existsM1>0 such that∀t ∈[0,T],∀m ∈N, Estimate 2 In the first approximate equation and second approximate equation of(3.3),respectively puttingω=(0),t=0 and=(0),t=0,using the Schwarz inequality,compatibility conditons (2.1)and the value inequality,we see that there existsM2>0 such that∀t ∈[0,T],∀m ∈N, Estimate 3 Let us fixt,ξ >0 such thatξ Uniqueness Let (u,v),(,)be two solutions of (1.1)-(1.3)with the same initial data.Then writingz=u−,=v−,taking the difference (3.3)withu=u,v=vandu=,v=,respectively replacingω,byz,and then making a computation of addition,using the mean value theorem and the Young inequalities combined with Estimate 1 and Estimate 3,we can find a constantC >0,∀t ∈(0,T), From Gronwall’s Lemma,we see thatu=,v=. Sinceuxx,vxx,uxxt,vxxt ∈ L2(0,∞;L2(Ω)),we getu,v ∈ C0([0,∞);V).Similarly,u,v ∈C1([0,∞);U).Considerun,vnsatisfying (1.1)-(1.3)where|un0−u0|H2(Ω)→0,|vn0−v0|H2(Ω)→0,|un1−u1|H1(Ω)→0,|vn1−v1|H1(Ω)→0,un0,vn0∈H4(Ω),un1,vn1∈H4(Ω)and satisfy the appropriate compatibility conditions on the boundary.By the standard linear semigroup method,it can be shown that the problem (1.1)-(1.3)admits a solution(un,vn)∈W ×W.The proof of Theorem 3.1 is completed. Theorem 3.2If the initial data(u0,u1,v0,v1)∈H0,there exists a unique weak solution of problem (1.1)-(1.3)which depends continuously on initial data with respect to the norms ofH0. ProofLet us consider (u0,u1,v0,v1)∈H0.SinceH1is dense inH0,then exists(u0µ,u1µ,v0µ,v1µ)∈H1,such that For eachµ ∈N,there exists (uµ,vµ),smooth solution of the initial boundary value problem(1.1)-(1.3),which satisfies Respectively multiplying the first equation byutµand the second equation byvtµin(3.5),integrating overΩ,taking the sum,considering the argument used in the estimate of the existence of solution,we can find a constantC0>0 independent ofµ∈N such that We can pass to the limit using standard arguments in order to obtain Theorem 3.2 is proved. Remark 3.1Let us setS(t)(u0,u1,v0,v1)(u,ut,v,vt),∀t ≥0.The operatorS(t)defined inH0mapsH0into itself,we see thatS(t)is a nonlinearC0-semigroup onH0. Lemma 4.1[14]Assume that for any bounded positive invariant setB ∈Hand anyε>0,there existsT=T(ε,B)such that whereφT:H ×H→R,satisfies for any sequence{zn}∈B, ThenS(t)is asymptotically smooth. Lemma 4.2[14]LetS(t)be a dissipativeC0-semigroup defined on a metric spaceH;thenS(t)has a compact global attractor inHif and only if it is asymptotically smooth inH. Theorem 4.1Assume the hypotheses of Theorem 3.2 andρ=r=0 hold,the corresponding semigroupS(t)of problem (1.1)-(1.3)has an absorbing set inH0. ProofLet us fix an arbitrary bounded setB ∈H0and consider the solutions of problem(1.1)-(1.3)given by (u(t),ut(t),v(t),vt(t))=S(t)(u0,u1,v0,v1)with (u0,u1,v0,v1)∈B.Sinceu(0,t)=ux(L,t)=uxx(0,t)=0,the following inequalities hold: We can calculate the total energy functional Let us define In the first equation and the second equation of(1.1),respectively multiplying byut+εuandvt+εv,then integrating overΩand taking the sum,we have In the following,we estimate (4.3). Using (2.2)and (4.1),we obtain Using(2.4),we obtain Using (2.5)andr=0,we obtain Using (2.6),we obtain Considering thatN(·)∈C1(R),there exists a constantC >0,such that Then inserting (4.4)-(4.8)into (4.3),we obtain Taking 0<ε ≤min {p1/9m21L3,p2/9m22L3,α/3L,αk1/(3k1+C),αk2/(3k2+C),1}=ε0small enough,we get Since we have 1−6k1L3−2LCk1≥0,withk1≥0 sufficiently small,we can get Since we have 1−6k2L3−2LCk2≥0,withk2≥0 sufficiently small,we can get Then inserting (4.10)-(4.12)into (4.9),we obtain Let us define modified energy functional Then we obtain Since using (2.2),we obtain and using (4.13),we obtain Let us set From (4.1),we have forεsufficiently small enough, Let us defineL3=1+2ε(L2+L4),L4=2L0+L1+L2+L4(||p||22+||q||22).Inserting (4.16)into (4.14),we have Applying Gronwall’s inequality,we obtain Since the given invariant setBis bounded,(0)is also bounded.Then there existstB >0 large enough such that∀t>tB, Then from (4.15)we have∀t>tB, This shows that is an absorbing set forS(t)inH0.The proof of Theorem 4.1 is completed. Theorem 4.2Assume the hypotheses of Theorem 3.2 andρ=r=0 hold,the corresponding semigroupS(t)of problem (1.1)-(1.3)is asymptotic compactness inH0. ProofGiven initial data (u0,u1,v0,v1) andin a bounded invariant setB ∈H0,let (u,v),(,) be the corresponding weak solution of problem (1.1)-(1.3).Then the differenceω=u −,=v −is a weak solution of where We can calculate the total energy functional and define Respectively multiply the first equation and the second equation of (4.17)byωt+µωand+.Then integrating overΩand taking the sum,we have In the following,let us estimate (4.19). From the assumption (2.3)andρ=0,we have Using (2.4),we obtain From the assumption (2.5)andr=0,we have From the assumption (2.6),we get Considering thatN(·)∈C1(R),there exists a constantC0>0 such that From the mean value theoremN(a2)−N(b2)≤N′(sup {a2,b2})|a−b||a+b|,we get Obviously,we get Substituting (4.20)-(4.26)into (4.19),we get Withµ≤2α/(7+4L)sufficiently small enough,we have DefiningFµ(t)=F(t)+µψ(t),we get For 0<µ≤min {2α/(7+4L),1/2L2} sufficiently small enough,we get Inserting (4.28)into (4.27),there exists a constantC1>0 such that From Gronwall’s lemma,we obtain Combining (4.28)and (4.29),there exists a constantCB >0,only depending on the size ofB,such that Givenε>0,we chooseTlarge such that and definedϕT:H0×H0→R as From (4.30)-(4.32),we have and consequently SoS(t)is asymptotically smooth inH0. In view of Lemma 4.2,Theorem 4.1 and Theorem 4.2,we have the main result. Theorem 4.3The corresponding semigroupS(t)of the problem (1.1)-(1.3)has a compact global attractor inH0.
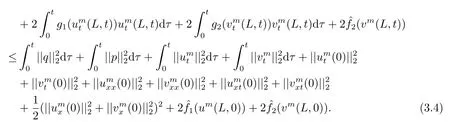






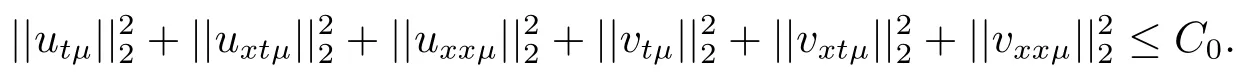


4.The Existence of Global Attractor

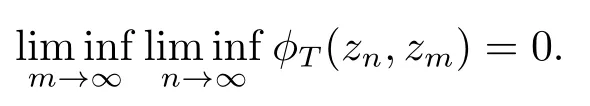



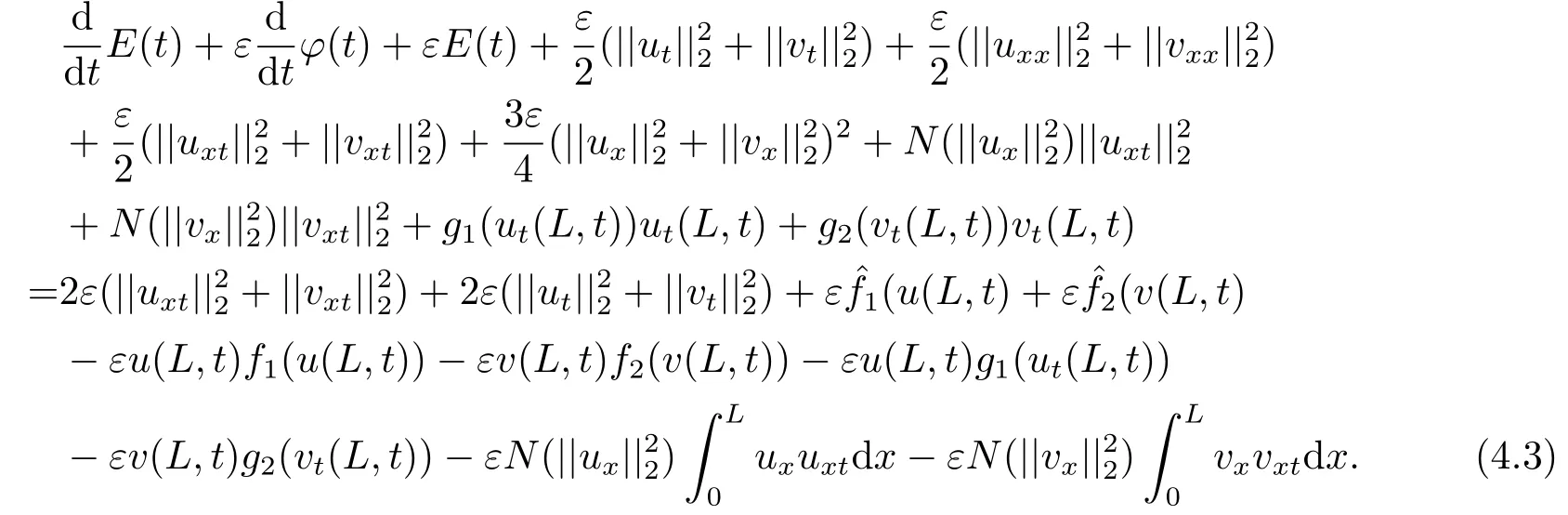






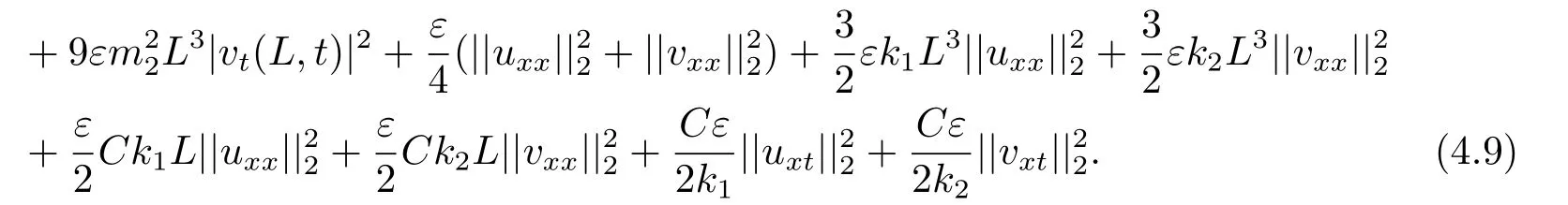



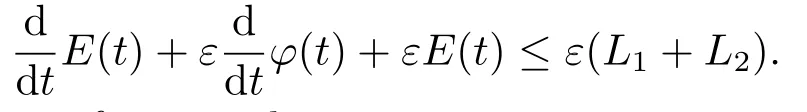










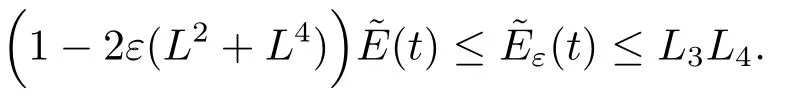
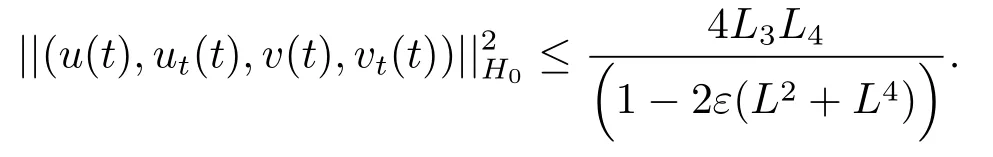





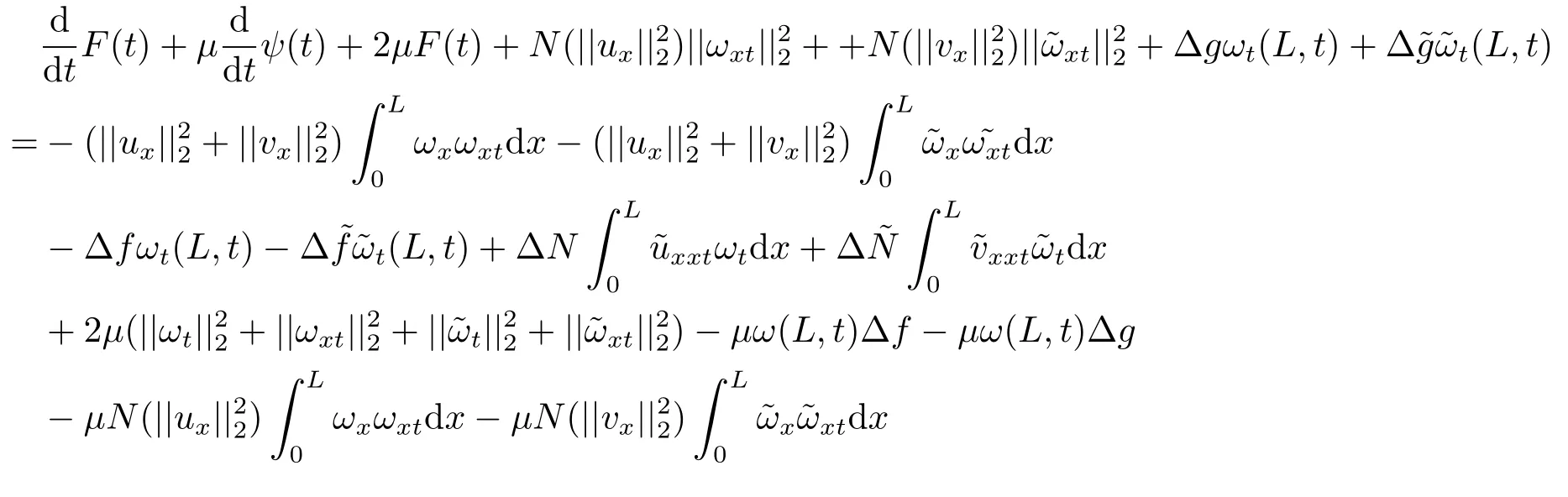









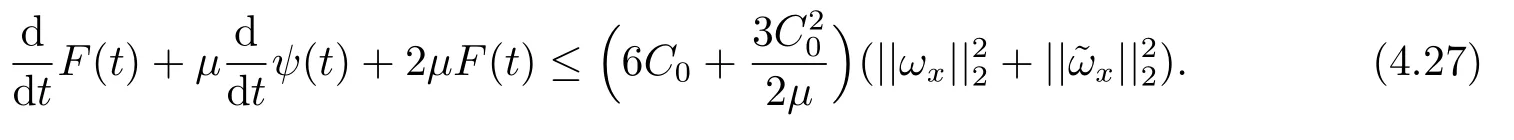
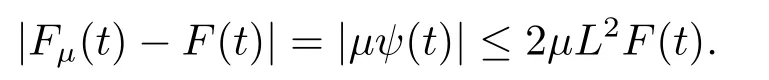







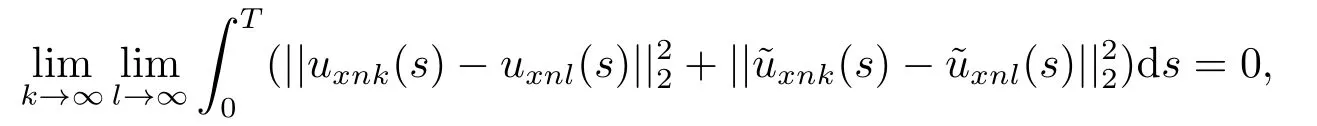

——李建文
- 应用数学的其它文章
- Threshold Dynamics of Discrete HIV Virus Model with Therapy
- Solvability for Fractional p-Laplacian Differential Equation with Integral Boundary Conditions at Resonance on Infinite Interval
- Existence and Uniqueness of Mild Solutions for Nonlinear Fractional Integro-Differential Evolution Equations
- 基于Markov链的税延型养老保险跨期效用
- 动态投资组合现金次可加风险度量的时间相容性
- 部分线性模型的模态正交经验似然推断

