一类冲击碰振系统的分岔及混沌演化分析

汪健龙李万祥

（兰州交通大学机电工程学院，兰州 730070）

一类冲击碰振系统的分岔及混沌演化分析

汪健龙†李万祥

（兰州交通大学机电工程学院，兰州 730070）

运用Poincaré映射理论与计算机仿真，研究了三自由度含间隙碰振系统的分岔和向混沌演化的道路.结果表明，在Hopf-flip余维二分岔点附近存在倍化分岔和Hopf分岔，不动点先发生倍化分岔形成周期2点，又经过Hopf分岔形成了概周期运动.Hopf-Hopf余维二分岔通过数值仿真展现了Hopf分岔、环面分岔以及由“近正方形”概周期吸引子转迁为混沌的奇异过程.通过对该类系统的研究，可以为工程实际中的含间隙碰振系统的优化设计提供理论参考.

Poincaré映射， 间隙， 碰振， 混沌， 余维二分岔

引言

含间隙的机械构件在工程实际中普遍存在，它是不可避免的.有间隙就会存在碰撞和冲击，这毫无疑问会对机械设备产生不利的影响.例如，零件组装时的间隙会影响系统的安全性和耐用性；齿轮、连杆、轴承等传动件间的间隙会降低传动效率.但是，一些机械设备是依靠碰撞振动来达到工作目的，比如振动落砂机、冲击振动成型机、振动筛等.正是由于碰撞的存在，机械系统的动力学行为会变得更为复杂，甚至系统的拓扑结构都会改变.

学者们在这一方面进行了研究，并且得出了一些鲜明的结论.文献［1］以两自由度分段线性系统为研究对象，分析了在一定的参数下系统会出现Neimark-Sacker分岔和倍化分岔.文献［2］建立了转子-密封系统的模型，研究了气流激振力下系统的亚谐共振问题.文献［3］研究了两自由度碰撞振动系统的Hopf-flip余维二分岔，分析了不动点的概周期分岔与倍化分岔.文献［4］研究了一类实际模型冲击振动成型机的周期运动以及发生的Hopfflip余维二分岔.数值仿真了其在该类分岔条件下的动力学行为，并演化了通向混沌的过程.文献［5］探讨了当碰撞振动系统发生余维二分岔时，周期1、2点的Hopf分岔现象是存在的，并揭示了概周期运动经环面倍化与锁相转迁为混沌的过程.文献［6］以一单自由度含间隙的弹性约束系统为研究模型，通过数值计算证明了Hopf分岔在单自由度系统中的存在性.

本文以工程实际为出发点，建立了一类含间隙的碰振模型，求出了其周期解及六维的Poincaré映射.用Matlab编程仿真系统的周期运动［7-8］与过渡到混沌的过程.文中主要研究了余维二分岔点［9］附近复杂的动力学特性，用Poincaré映射投影图、相图、时间历程图、分岔图形象地展示了系统随参数变化而出现的分岔［10-11］行为.

1 力学模型及运动微分方程

图1表示存在间隙的三自由度相对碰撞振动系统的动力学模型，工程实际中许多部件的碰撞可认为此模型的简化.如图1所示整个模型由质量块、弹簧和阻尼器相连接而成.弹簧刚度分别为K1、K2、K3、K4，阻尼系数分别为C1、C2、C3、C4，假定质量块M1、M2、M3只在垂向运动，三个振子受到的简谐激振力为Pisin（ΩT+τ）（i＝1，2，3），当满足关系X1-X3＝Δ时，质量块M1将与质量块M3发生碰撞.这里的阻尼为Rayleigh型比例阻尼，碰撞过取决于碰撞恢复系数R，不计碰撞时间.

在连续两次碰撞之间，该碰振系统无量纲化的运动微分方程表示为：

图1 系统力学模型图Fig.1 Schematic of the system mechanicalmodel

振子M1与M3碰撞时的冲击方程及R为：

式中，下标“+”和“-”分别表示碰撞瞬时前后.

下面对方程（1）解耦，令ψ为正则模态矩阵，ωn1和ωn2是无碰撞振动情况下系统的固有频率.这里取ψ为变换矩阵，做如下的坐标变换

式中，X＝（x1，x2）T；ξ＝（ξ1，ξ2）T.

经过坐标变换，方程（1）可以写为：

式中，ψij为正则模态矩阵ψ的元素和bj是积分常数，可通过系统的初始条件和模态参数确定；Aj和Bj为振幅常数，可通过稳态解回代求得（j＝1，2，3）.

2 碰撞振动系统的Poincaré映射

为了分析碰撞振动系统的概周期运动和相关的分岔问题，通常要确定Poincaré映射，并且基于以上周期解，可以写出扰动解.定义截面σ为：

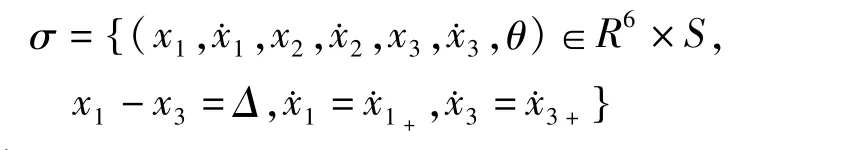
式中，θ＝ωtmod2π.

这里将截面σ作为Poincaré截面.建立周期运动的映射方程：

式中，v∈R1；X＝X*+ΔX，X′＝X*+ΔX′，X*＝表示位于在Poincaré截面σ上的周期n单碰撞不动点，ΔX与ΔX′是扰动.

文中用q＝p／n来表示周期运动，其中n表示周期数，p表示对应的碰撞次数.当系统受到扰动后，在M1与M3碰撞后的瞬时，令时间t为0，那么下一次发生碰撞前的时间为：

由边界条件可推得周期运动的Poincaré映射为：

式中，x10表示未受扰动时质量块M1在t＝0时刻碰后的位移，x20同上.且

从而建立Poincaré映射，简要地表示成：

（11）式位于不动点处的雅克比矩阵为

式中，ν∈R表示分岔参数，为系统参数之一.

利用（12）式的特征值可判别系统周期运动的稳定性.若线性化矩阵Df（v，0）的全部特征值都位于复平面单位圆的内部，那么周期运动是稳定的.只要特征值穿越单位圆的情况存在，系统的周期运动将会出现分岔.一般来说，由特征值穿越单位圆的位置和数量来决定分岔为何种类型.

3 数值仿真

选择一组无量纲系统参数值：

um3＝1.75，um2＝0.65，uk2＝1.15，uk3＝0.016，uk4＝1.05，ζ＝0.002，R＝0.65，δ＝0.025.将激励频率ω作为分岔参数，特征值的穿越趋势见图2，依据判断条件可知满足Hopf-flip余维二分岔.即有一对复共轭特征值和一个-1的实特征值横截单位圆周，剩下的特征值都位于单位圆的内部.

图2 特征值穿越单位圆周Fig.2 Variation of eigenvalues inside the unit circle

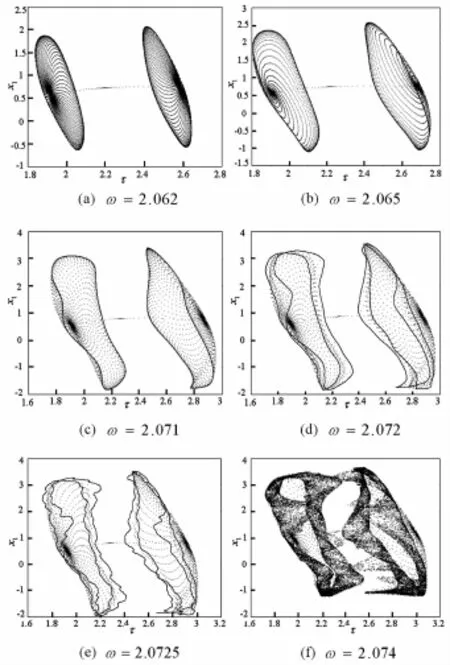
图3 Poincaré映射投影图Fig.3 Projection draw of Poincarémap

进行数值编程仿真，当ω＜ωc＝2.056时，该系统处于稳定的q＝1／1周期运动，在Poincaré截面上则为一个q＝1／1不动点；随着激励频率ω的递增，当ω＝2.062时，稳定的q＝1／1不动点发生倍化分岔与Hopf分岔，变为T2／2吸引不变环，如图3（a）、3（b）；若激励频率进一步增加，吸引不变圈的环面发生振荡，如图3（c）；当激励频率ω＝2.072时，T2／2环失稳，发生了环面倍化，在Poincaré截面上形成2T2／2吸引不变环，如图3（d）；若激励频率ω继续递增，2T2／2环面发生振荡，如图3（e）；当激励频率ω＝2.074时，系统经环面倍化转迁为混沌，如图3（f）.

为了进一步分析系统处于混沌运动时的动力学行为，在ω＝2.074的条件下，通过编程分别仿真了3个质量块的相图和时间历程图，如图4.由于质块M1和M3在运动的过程中会发生碰撞，所以其相图与质块M2的相图是有区别的.从图4（a）、4（e）中，可知碰撞时“位移不变，速度突变”.从时间历程图可以看出，此时系统运动呈非周期性，即处于混沌运动.

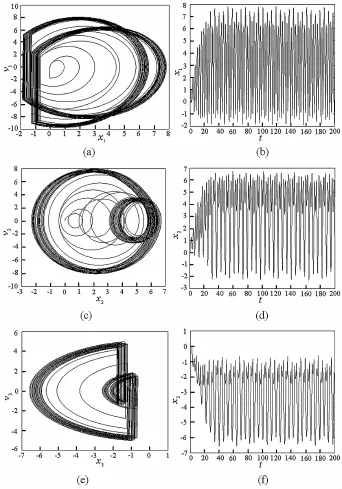
图4 ω＝2.074，相图和时间历程图Fig.4 Phase diagrams and time history diagrams whenω＝2.074

取无量纲系统参数值为：um3＝1.1，um2＝0.44，uk2＝1.15，uk3＝0.59，uk4＝0.5，ζ＝0.0，R＝0.81，δ＝0.026.以激励频率ω作为分岔参数，数值仿真不动点邻域内的特征值发展趋势，系统特征值的穿越见图5.当ω逐渐减小经过ωc＝1.338时，出现了两对复共轭特征值穿越情况，满足Hopf-Hopf余维二分岔的条件.图6（a）为分岔图，从图中可以看出系统的分岔行为，图6（b）为图6（a）的局部放大图.在分岔图中难以辨别概周期运动和混沌运动，因此还需进行进一步的分析.

图5 特征值穿越单位圆周Fig.5 Variation of eigenvalues inside the unit circle

图6 分岔图Fig.6 Bifurcation diagrams

在这组参数值下进行数值仿真，如图7所示.随着激励频率ω的减小，当ω＝1.338时，稳定的q＝1／1不动点发生Hopf分岔，Poincaré截面上形成一个不变圈，系统呈现概周期运动，如图7（a）所示；当激励频率继续减小时，吸引不变圈的光滑性逐渐减弱并发生振荡，如图7（b）；当激励频率ω＝1.32687时，概周期吸引子发生环面分岔，变为“带状”型，如图7（c）；随着激励频率ω进一步远离分岔点时，产生了奇特的“近正方形”概周期吸引子，如图7（d）；当激励频率ω＝1.321时，退化出5T1／1吸引环，如图7（e）；继续减小激励频率ω，吸引不变环转化为半吸引的，运动最终经半吸引不变环通向混沌，如图7（f）.图8为ω＝1.3208时，质量块M1的相图和时间历程图，由图可知系统处于混沌状态，从而证实了前面分析方法的正确性.

图7 Poincaré映射投影Fig.7 Projection draw of Poincarémap

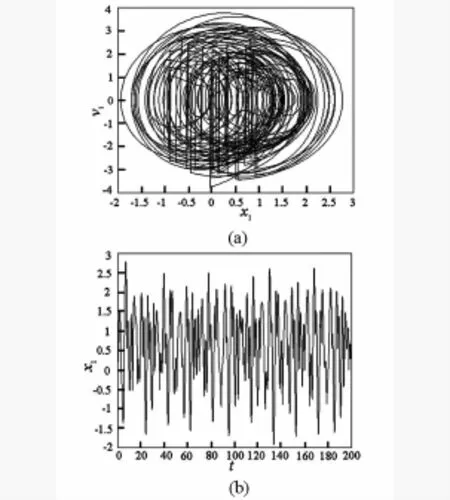
图8 M1的相图和时间历程图Fig.8 Phase diagrams and time history diagrams ofM1

4 结论

（1）通过数值仿真揭示了含间隙三自由度系统的周期运动转迁为混沌运动的两条道路.在Hopf-flip分岔中即存在倍化分岔，也存在周期2的Hopf分岔和环面倍化.当系统发生Hopf-Hopf分岔时，可通过环面分岔形成非常规“近正方形”概周期吸引子，展现了向混沌演化的精彩过程.

（2）由分析可知，系统参数的选取对机械的振动特性有很大影响，当参数变化时，机械系统可能产生复杂的分岔与混沌现象.因此，文中的参数范围可以作为机械系统优化设计的依据.

（3）文中的研究方法与所得的结论可以推广到其它含间隙的多自由度碰撞振动模型，为这些模型的研究分析提供有益参考，同时也是混沌控制的基础理论.

1 徐慧东，谢建华.一类两自由度分段线性非光滑系统分岔与混沌.振动工程学报，2008，21（3）：279～285（Xu H D，Xie JH.Bifurcation and chaos of a two-degree-of-freedom non-smooth system with piecewise-linearity.Journal of Vibration Engineering，2008，21（3）：279～285（in Chinese））

2 李忠刚，陈予恕，陈照波等.转子-密封系统中气流激振力的非线性动力学特性分析.动力学与控制学报，2013，11（2）：126～132（Li ZG，Chen Y S，Chen Z B，et al.Nonlinear dynamic characteristics analysis of the gas exciting force in the rotor-seal system.Journal of Dynamics and Control，2013，11（2）：126～132（in Chinese））

3 Ding W C，Xie JH.Interaction of Hopf and period doubling bifurcation of a vibro-impact system.Journel of Sound and Vibration，2004，275（1-2）：29～45

4 罗冠炜，张艳龙，张建刚等.冲击振动成型机周期运动的Hopf-flip余维二分岔与混沌.工程力学，2007，24（9）：140～147（Luo GW，Zhang Y L，Zhang JG，et al.Codimension two bifurcation and chaos of a vibro-impact forming machine associated with Hopf-flip case.Engineering Mechanics，2007，24（9）：140～147（in Chinese））

5 Wen G L，Codimension-2 Hopf bifurcation of a two-degreeof-freedom vibro-impact system.Journel of Sound and Vibration，2001，242（3）：475～485

6 李万祥，边红丽，蒋湘云.含间隙弹性约束系统的Hopf分岔与混沌研究.机械科学与技术，2004，23（10）：1211～1213（LiW X，Bian H L，Jiang X Y.Hopf Bifurcation and chaos ofa system with a pair of symm-etric set-up elastic stops.Mechanical Science and Technology，2004，23（10）：1211～1213（in Chinese））

7 周伟，褚衍东，俞建宁等.一类两自由度含间隙系统的Hopf分叉.动力学与控制学报，2008，6（3）：235～238（Zhou W，Chu Y D，Yu JN，et al.The Hopf bifurcation of two-degree-of-freedom system with clear-ance.Journal of Dynamics and Control，2008，6（3）：235～23（in Chinese））

8 曹登庆，舒仲周.存在间隙的多自由度系统的周期运动及Robust稳定性.力学学报，1997，29（1）：74～82（Cao D Q，Shu Z Z.Periodic motions and Robust stability of the multi-degree-of-freedom systems with clearances.Chinese Journal of Theoreticaland Applied Mechanics，1997，29（1）：74～82（in Chinese））

9 张艳龙.多自由度冲击振动系统的周期运动和分岔［硕士学位论文］.兰州：兰州交通大学，2006（Zhang Y L.Periodic motions and bifurcations of multi-degree-of-freedom vibro-impact system［Master Thesis］.Lanzhou：Lanzhou Jiaotong University，2006（in Chinese））

10 吕小红，罗冠炜.冲击钻进系统的亚谐振动与分岔.工程力学，2013，30（3）：383～389（Lv X H，Luo G W.Subhar-monic vibrations and bifurcations of impact-progressive system.Engineering Mechanics，2013，30（3）：383～389（in Chinese））

11 王福新，胡海岩.对称分段线性系统主共振的分叉.南京航空航天大学学报，1997，29（3）：283～288（Wang F X，Hu H Y.Bifurcations of primary resonance of harmonically forced symmetrical piecewise-linear systems.Journal of Nanjing University of Aeronauticsand Astronautics，1997， 29（3）：283～288（in Chinese） ）

ANALYSISOF ROUTES TO CHAOS AND BIFURCATION OF A VIBRO-IMPACT SYSTEM

Wang Jianlong†LiWanxiang
（School of Mechatronic Engineering，Lanzhou Jiaotong University，Lanzhou730070，China）

The bifurcation and the routes to chaos of the three-degree-of-freedom vibro-impact system with clearance are investigated using Poincarémapping and the computer simulation in this paper.The results show that flip bifurcation and Hopf bifurcation exist close to the bifurcation point of the Hopf-flip codimension two bifurcation.In the fixed point，the period two point is formed when Flip bifurcation firstly takes place，and the quasiperiodic motion occurs after Hopf bifurcation.It is revealed that Hopf bifurcation，torus bifurcation and the chaos evolution of the“subquadrate”quasi-period attractor through the numerical simulations are exhibited in Hopf-Hopf codimension two bifurcations.The study on this vibro-impact system with clearance provides the essential reference for its future optimize design.

Poincarémap， clearance， vibro-impact， chaos， codimension two bifurcation

10.6052／1672-6553-2015-74

2015-10-03收到第1稿，2015-10-22收到修改稿.

†通讯作者E-mail：jlwang321＠163.com

Received 3 October 2015，revised 22 October 2015.

†Corresponding author E-mail：jlwang321＠163.com