时滞反馈作用下压电梁的参数共振分析*

彭剑李禄欣马建军

（1.湖南科技大学土木工程学院，湘潭 411201）（2.河南科技大学土木工程学院，洛阳 471023）

时滞反馈作用下压电梁的参数共振分析*

彭剑1†李禄欣1马建军2

（1.湖南科技大学土木工程学院，湘潭 411201）（2.河南科技大学土木工程学院，洛阳 471023）

基于Hamilton原理建立了受控压电梁的参数振动方程，研究了轴向激励压电梁时滞速度反馈控制的主参数共振.采用非线性振动的多尺度法研究了压电梁的亚谐波主参数共振，并对其稳定域进行分析.通过算例分析得到了不同时滞，控制增益，轴力影响下压电梁参数共振的稳定域和时程曲线.结果表明：时滞值增大，系统承受轴向力减小，相对于控制增益则反之.同时，随着轴向力增大，在一定范围内主动阻尼增加，时滞反馈能有效降低响应幅值.随着时滞值增大，减振效果变差.

压电梁， 时滞， 稳定性， 参数共振

引言

梁结构作为一个基本构件，广泛应用于土木、机械和航空航天等工程领域.在承受外荷载作用下，易发生大幅振动［1-2］，影响系统的正常工作.因此，梁结构的大幅振动控制问题亟待解决.

国内外学者从理论研究、实验分析等方面开展了研究［3］.特别值得指出的是，时滞反馈控制技术的发展为梁结构的振动控制提供了新的思路［4-10］.王在华和胡海岩［4］对时滞动力系统的理论和应用研究现状做了详尽的阐述.赵艳影和徐鉴［5］研究了时滞非线性动力吸振器的减振机理.Daqaq［6］研究了时滞反馈作用下悬臂梁的非线性振动.刘铭等［7］对中立型时滞反馈扭转控制系统的稳定性进行了分析.贾雁兵等［8］研究了异质性和时滞作用下神经元网络的共振动力学.李欣业等［9］研究了陀螺系统的受迫振动并采用时滞反馈进行振动控制.冯志宏和霍睿［10］对压电耦合悬臂梁的时滞反馈控制及稳定性进行了分析.彭剑等［11］研究了时滞反馈及轴力作用下弹性梁的非线性振动.

本文采用时滞速度反馈控制对受轴向激励作用下的压电梁的主参数共振开展研究，分析控制系统中关键参数对受控系统稳定域及共振响应的影响.

1 运动方程

简支梁如图1所示，截面形状为矩形，压电材料良好，粘贴在梁表面，梁端沿轴线方向受激振力P（t）＝P0+PtcosΩt作用，P0为轴力初值，Pt为轴力幅值，Ω为激振轴力频率.建立坐标系如图1所示，假设梁不可伸长且忽略扭转和剪切变形.

图1 轴向激励下的压电梁的理论模型Fig.1 Model of a piezoelectric beam subjected to axial excitation

根据Hamilton变分原理：

其中，δ为变分符号，T和U为整体结构的动能和势能，δWP为外力虚功.考虑梁横向位移w的一阶展开式，将其表示为：

其中，q（t）为位移幅值，即广义坐标，L为梁长.则动能、势能和外力功分别表示为［3］：

c为阻尼系数，h为基梁厚底，b表示压电层的宽，m为基梁和压电片单位长度的质量，V0为外加电压，hp为压电片厚度，e31为压电常数.将方程（3）～（5）代入方程（1），并对广义坐标w求变分，得到结构的非线性运动方程如下：

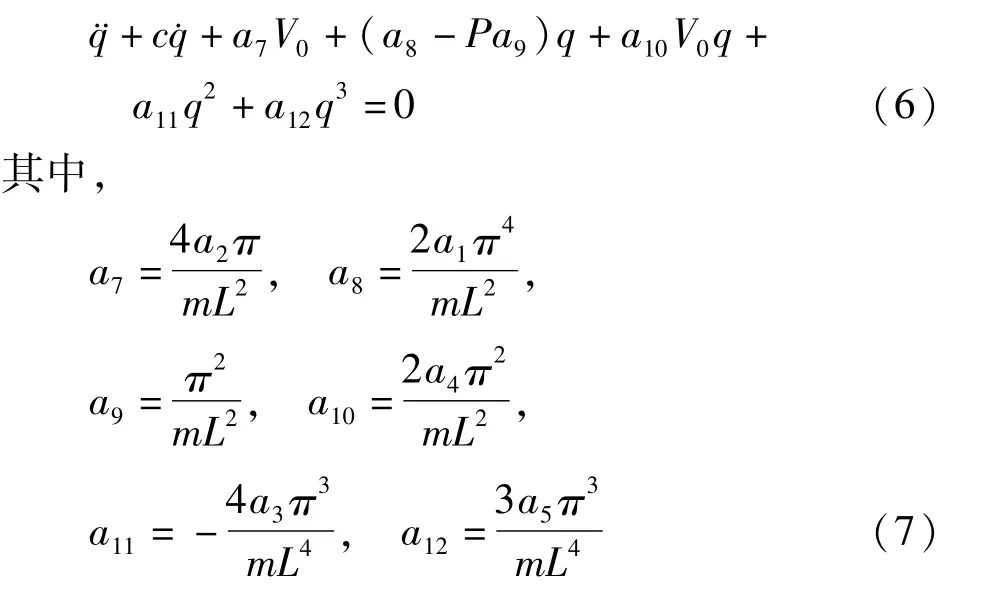
根据压电材料控制机理，采用速度传感器测量梁结构某一点x0处的速度并传给控制器，采用时滞速度反馈控制策略施加沿压电作动器控制电压［6］，即：

式中k为反馈控制增益.则受控系统运动运动方程为：

2 参数振动分析

下面运用多尺度法［12］对时滞反馈压电梁的参数共振进行分析.将P（t）代入方程（9），并整理如下：

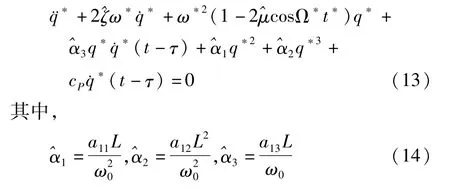
为书写方便，在以下分析中略去方程中的星号.同时将系数调整为：

其中ε为小扰动参数.设方程（13）的解为：

方程（16）的通解可以写为：

将An表示成极坐标其中a和nβn是关于T1的实函数.分离实虚部，可得：

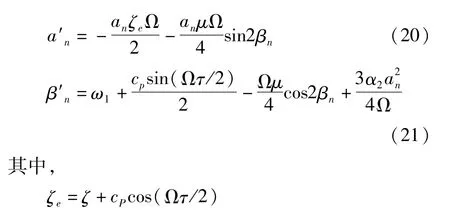
令a′n0＝γ′n0＝0则可得稳定解.考虑非平凡解，即an≠0，则由方程（20）和（21）可得：

将方程（22）代入方程（21），得到定常解的振幅为：

上式称为幅频曲线方程，反映了外激励和主动阻尼等对结构振动幅值的影响.

根据An为实函数的条件，由方程（23）得到结构运动稳定性条件如下：

3 算例分析

本节通过具体算例分析参数对结构参数共振的影响.梁和压电材料的几何和物理参数如下［3］.梁：弹性模量E＝71GPa，线密度ρ＝2710kg·m· s-2，长度L＝0.5m，宽度b＝0.01m，厚度h＝0.005 m.压电材料：弹性模量c＝126GPa，线密度ρP＝7500kg·m·s-2，压电系数e31＝-6.5cm-2，长度LP＝0.5m，宽度bP＝0.01m，厚度hP＝0.001m，x0＝L／2.

图2给出了时滞τ对压电梁参数共振稳定性的影响，纵坐标μ与轴力幅值Pt有关，此处P0＝120N.从图2中可以看到，当k＝2时，随着时滞值的减小，稳定性区域边界处于曲线的最低点附近向上移动.此时，2ω／Ω＝1附近上方移动，该点是亚谐波-主参数共振点，也就是说，给定控制增益，不同时滞下，结构稳定性区域发生变化并且相对亚谐波-主参数共振区有一定偏移.图3分析了控制增益k对压电梁参数共振的影响.当给定时滞τ＝π／4时，随着控制增益的增长，稳定区域边界线上移.值得注意的是：控制增益越大，结构所能承受的轴向力越大（限于屈曲荷载范围）.

图2 不同时滞时压电梁参数共振稳定性域Fig.2 Stability region of parametrically excited piezoelectric beam with different time delay

图3 不同控制增益时压电梁参数共振稳定性域Fig.3 Stability region of parametrically excited piezoelectric beam with different control gain

图4 轴力影响下压电梁参数共振稳定性域Fig.4 Stability region of parametrically excited piezoelectric beam with the effect of axial force

图4给出了无控和受控作用下轴力对压电梁参数共振的影响.可见，随着轴力的增大，稳定域边界线逐渐升高，同时可以看到，施加控制的稳定域较有降低，说明轴力增加，需较大的主动阻尼才能使结构处于稳定区域，而施加控制的效果明显.

图5～图7给出了无控和受控作用下压电梁参数振动响应的时程曲线.可以看出，采用时滞反馈控制后，响应幅值明显受到抑制，但随着时滞值的增大，结构响应也逐渐增大，甚至可能导致失稳.

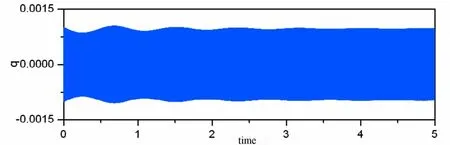
图5 无控梁的时程曲线Fig.5 Time history of an apiezoelectric beam without control

图6 k＝2，τ＝π／4时受控梁的时程曲线Fig.6 Time history of a controlled piezoelectric beam whenk＝2，τ＝π／4

图7 k＝2，τ＝π时受控梁的时程曲线Fig.7 Time history of a controlled piezoelectric beam whenk＝2，τ＝π

4 小结

本文研究了压电梁参数共振的时滞反馈控制，采用多尺度法得到了参数共振的稳定性曲线，分析了控制增益、时滞值、轴力等因素对稳定性区域的影响.得到结论如下：时滞反馈控制下，较小的时滞值和较大的控制增益结构能承受的轴向与激励越大.在稳定域内，增大控制增益有利于增大主动阻尼.结构主参数共振响应随着时滞的增大出现拍振，甚至可能失稳.

1 Zhang W，Wang F X，Zu JW.Local bifurcations and codimension-3 degenerate bifurcations of a quintic nonlinear beam under parametric excitation.Chaos，Solitons and Fractals，2005，24（4）：977～998

2 李海涛，秦卫阳，田瑞兰.随机及移动荷载激励下弹性梁分岔与混沌.动力学与控制学报，2015，13（6）：417～422（Li H T，Qin W Y，Tian R L.Bifurcation and chaos of beam subjected tomoving loads and random excitations.Journal of Dynamics and Control，2015，13（6）：417～422（in Chinese））

3 李凤明，刘春川.非线性梁结构的参数振动稳定性及其主动控制.应用数学与力学，2012，33（11）：1284～1293（Li FM，Liu C C.Parametric vibration stability and active control of nonlinear beams.Applied Mathematics and Mechanics，2012，33（11）：1284～1293（in Chinese））

4 王在华，胡海岩.时滞动力系统的稳定性与分岔：从理论走向应用.力学进展，2013，43（1）：1～20（Wang Z H，Hu H Y.Stability and bifurcation of delayed dynamics systems：From theory to application，2013，43（1）：1～20（in Chinese））

5 赵艳影，徐鉴.时滞非线性动力吸振器的减振机理.力学学报，2008，40（1）：98～105（Zhao Y Y，Xu J.Mechanism analysis of delayed nonlinear vibration absorber.Chinese Journal of Theoretical and Applied Mechanics，2008，40（1）：98～105（in Chinese））

6 Daqaq M F，Alhazza K A，Arafat H N.Non-linear vibrations of cantilever beamswith feedback delays.International Journal of Non-Linear Mechanics，2008，43：962～978

7 刘铭，徐晓峰，张春蕊.中立型时滞反馈扭转控制系统的稳定性分析.动力学与控制学报，2015，13（6）：449～453（Liu M，Xu X F，Zhang CR.Stability analysis of delayed torsional vibration system of neutral type.Journal of Dynamics and Control，2015，13（6）：449～453（in Chinese））

8 贾雁兵，杨晓丽，孙中奎.异质性和时滞作用下神经元网络的共振动力学.动力学与控制学报，2014，12（1）：86～91（Jia Y B，Yang X L，Sun ZK.Impactof diversity and delays on the resonance dynamics of neuronal networks.Journal of Dynamics and Control，2014，12（1）：86～91（in Chinese））

9 李欣业，张利娟，张华彪.陀螺系统的受迫振动及其时滞反馈控制.振动与冲击，2012，31（9）：63～68（Li XY，Zhang L J，Zhang H B.Forced vibration of a gyroscope system and its delayed feedback control.Journal of Vibration and Shock，2012，31（9）：63～68（in Chinese））

10 冯志宏，霍睿.压电耦合悬臂梁的时滞反馈控制及稳定性分析.振动与冲击，2011，30（6）：181～184（Feng Z H，Huo R.Time-delay feedback control and stability analysis of piezoelectric-coupling cantilever beam.Journal of Vibration and Shock，2011，30（6）：181～184（in Chinese））

11 彭剑，赵珧冰，王连华.时滞反馈及轴力作用下弹性梁的非线性振动.湖南大学学报（自然科学版），2013，40（9）：30～36（Peng J，Zhao Y B，Wang L H.Nonlinear vibrations of elastic beams subjected to axial force and delayed-feedback.Journal of Hunan University（Naturnal Science），2013，40（9）：30～36（in Chinese））

12 Nayfeh A H.Linear and nonlinear structure mechanics.New York：Wiley Interscience，2004

PARAMETRIC RESONANCEOF PIEZOELECTRIC BEAMS W ITH TIME-DELAYED FEEDBACK*

Peng Jian1†Li Luxin1Ma Jianjun2
（1.School of Civil Engineering，Hunan University of Science and Technology，Xiangtan411201，China）
（2.College of Civil Engineering，Henan University of Science and Technology，Luoyang471023，China）

The primary parametric resonance of the time-delayed velocity feedback control on piezoelectric beams under axial excitation is studied.Based on Hamilton principle，the parameter vibration equations of the controlled piezoelectric beam are obtained.Themulti-scale method of the nonlinear vibration is used to study the subharmonic primary parameter resonance on the piezoelectric beam，and its stability regions are examined.The numerical example is given to investigate the effects of time delays，control gain and axial force on the stability region and obtain the time history curves of the primary parametric resonance on piezoelectric beams.The results show that the increase of time delay leads to the reduction of the axial force of the system，while the control gain exhibits opposite effect.Moreover，with the increase of the axial force，the active damping increases in a certain range，and the time-delayed feedback can effectively reduce the response amplitude.

piezoelectric beams， time delay， stability， parametric resonance

10.6052／1672-6553-2016-27

2016-1-20收到第1稿，2016-3-1收到修改稿.

*国家重点基础研究发展计划（973计划）项目（2015CB057702）、国家自然科学基金（11402085，11502072）和湖南省教育厅资助项目（14C0464）

†通讯作者E-mail：pengjian＠hnu.edu.cn

Received 20 January 2016，revised 1 March 2016.

*The project supported by the Natural Natural Science Foundation of China（2015CB057702），National Natural Science Foundation of China（11402085，11502072），Scientific Research Fund of Hunan Provincal Education Dapartment（14C0464）

†Corresponding author E-mail：pengjian＠hnu.edu.cn