二阶自治广义Birkhoff系统的奇点分析*

曹秋鹏陈向炜

（1.苏州科技学院数理学院，苏州 215009）（2.商丘师范学院物理与电气信息学院，商丘 476000）

二阶自治广义Birkhoff系统的奇点分析*

曹秋鹏1陈向炜2†

（1.苏州科技学院数理学院，苏州 215009）（2.商丘师范学院物理与电气信息学院，商丘 476000）

建立二阶自治广义Birkhoff系统的微分方程.给出该系统的线性化方程，得到该线性方程转化为梯度系统的条件，利用梯度系统的性质对线性系统的奇点进行了分析，然后再利用Perron定理探讨了相应的非线性系统的奇点类型.结果表明，如果线性系统能成为梯度系统，那么相应的非线性系统的奇点可能是结点或者鞍点.

广义Birkhoff系统， 梯度系统， 奇点

引言

微分方程定性理论的研究，一直是非线性动力学的热点问题［1］.迄今仍以二阶微分力学方程为主，主要内容是分析解的存在性，周期解，奇点性质，极限环个数，分岔和混沌等［2］.Birkhoff系统是Hamilton系统的自然推广，对Birkhoff系统定性理论的研究不仅具有理论意义还有实际应用价值.目前，高阶非完整系统的广义Birkhoff表示以及Birkhoff框架下的变分算法的研究取得重要进展［3-4］.对Birkhoff系统定性理论的研究已取得了一些重要成果［5-7］.梯度系统特别适合用Lyapunov函数来研究稳定性问题［8］.文献［9］提出了四类常见的梯度系统.如果力学系统可以转化成梯度系统，我们可以运用梯度系统的性质来研究系统的积分及其解的稳定性.梯度系统的研究已取得了一些重要成果，尤其是各类力学系统的通常梯度表示和斜梯度表示［10-12］.本文利用梯度系统的性质对二阶自治广义Birkhoff系统的奇点进行了分析，得到了该系统的奇点类型.

1 二阶自治广义Birkhoff系统的微分方程

广义Birkhoff系统微分方程为：

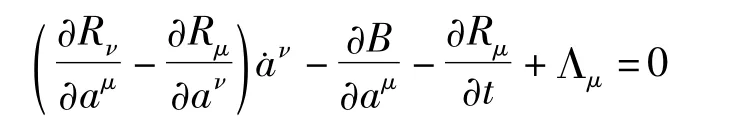
其中B＝B（t，a）是Birkhoff函数，Rμ＝Rμ（t，a）是Birkhoff函数组，Λμ＝Λμ（t，a）是附加项.对于二阶自治广义Birkhoff系统有形式：

这里的函数B，Rμ和Λμ都不显含时间t.设系统是非奇异的即

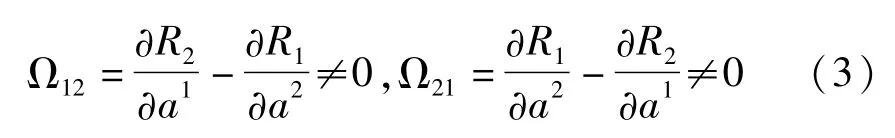
本文只考虑二阶自治广义Birkhoff系统（0，0）点的奇点类型.若（0，0）点是系统（4）的奇点，将系统（4）写成

2 线性化系统的奇点类型

2.1线性化系统

显然系统（4）在其奇点（0，0）处的线性化方程为：

为方便我们的讨论将（6）写成

本文我们考虑

显然当且仅当（9）式成立的时候，方程（7）有唯一的奇点（0，0）.

2.2 线性化系统的梯度表示

梯度系统有形式：

其中V＝V（x）称做该系统的势函数.

由文献［13］我们得到方程（7）成为梯度系统的条件.

性质1如果（7）满足条件

可以找到函数V使得

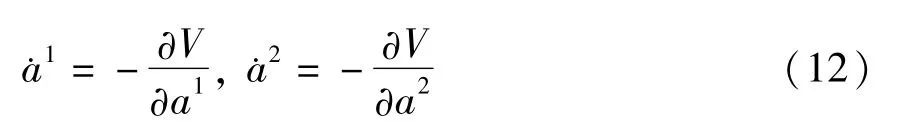
此时（7）成为一个梯度系统.

证明：因为有（11）成立，将（7）式代入（11），得到

将（13）式代入（7），得到

这时我们取函数V（a）为

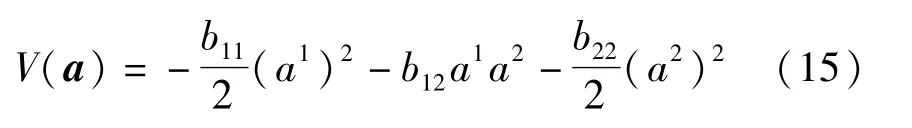
显然

此时（7）成为一个梯度系统.

梯度系统有一条重要的性质，即

性质2对于梯度系统（10），其任一平衡点的线性化系统只有实特征值.

我们可以用性质2来研究化成梯度系统的各力学线性系统的原点的奇点类型.

2.3 线性化系统的奇点类型

由2.2中的性质2可以得到下面的一条性质，即

性质3如果（7）为梯度系统，则其特征值只可能为同号实根或异号实根，不存在0根.

证明：由上面的性质2，只需要证明（7）不存在实特征值0.方程（7）的特征方程为

假设（17）有0根则应满足显然（18）与（9）矛盾，故（7）不可能有0特征值，性质3成立.

由微分方程奇点类型的相关知识［12］，我们由性质3得到以下结论：

性质4如果（7）是一个梯度系统，其特征值同号则奇点（0，0）为结点，其特征值异号则奇点（0，0）为鞍点，奇点（0，0）不可能为中心.

3 非线性系统的奇点类型

由Perron第一定理［14］知：

性质5 如果方程（5）中函数满足

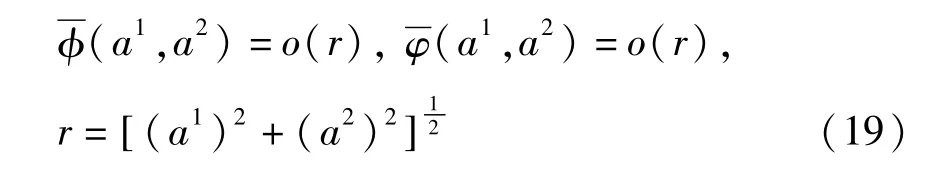
且在（0，0）邻域内存在连续一阶偏导数，若方程（6）中（0，0）点为（6）的结点或鞍点，则（0，0）点也是非线性方程（5）的同类奇点.

4 算例

例1二阶自治广义Birkhoff系统

试判断点（0，0）的奇点类型.

由（4）得该系统的微分方程

显然点（0，0）为系统（16）的奇点.要判定（0，0）的奇点类型，首先判断（0，0）为其线性化系统的何种奇点.由（6）得到系统（16）的线性化系统为：

明显方程（21）满足条件（11），则（21）是梯度系统.方程（21）的特征方程是

可得特征值为±1，是异号实根，则由性质4得对于线性化系统（21）其奇点（0，0）是鞍点.下面考虑带有高次项的非线性系统.对于系统（20）其高次项满足性质5的条件，则奇点（0，0）也是系统（20）的鞍点.

5 结论

梯度系统的性质不但可以用来研究力学系统解的稳定性及系统的积分，而且可以用来研究力学系统奇点的类型.本文给出了二阶自治广义Birkhoff系统奇点类型判定的梯度方法，如果二阶自治广义Birkhoff系统的线性系统能成为梯度系统，那么相应的非线性系统的奇点可能是结点或者鞍点.最后说明本文结论对于二阶自治Birkhoff系统也成立.

1 刘秉正，彭建华.非线性动力学.北京：高等教育出版社，2004（Liu B Z，Peng JH.Nonlinear dynamics.Beijing：Higher Education Press，2004（in Chinese））

2 Liu H T.Qualitative theory of differential equations.Hefei：University of Science and Technology of China Press，2009

3 宋端，崔金超，刘世兴，郭永新.高阶非完整系统的广义Birkhoff表示.动力学与控制学报，2013，11（2）：97～101（Song D，Cui JC，Liu S X，Guo Y X.Generalized Birkhoffian representation of high-order nonholonomic systems.Journal of Dynamics and Control，2013，11（2）：97～101（in Chinese））

4 刘世兴，李娜，刘畅.Birkhoff框架下Whittaker方程的离散变分算法.动力学与控制学报，2015，13（4）：246～249（Liu SX，Li N，Liu C.Discrete variational calculation of Whittaker equation in the Birkhoffian framework.Journal of Dynamics and Control，2015，13（4）：246～249（in Chinese））

5 陈向炜.Birkhoff系统的全局分析.开封：河南大学出版社，2002（Chen X W.Global analysis of Birkhoff system.Kaifeng：Henan University press，2002（in Chinese））

6 Li Y M，Mei F X.Stability formanifolds of equilibrium states of generalized Birkhoff system.Chinese Physics B，2010，19（8）：080302

7 李彦敏，陈向炜.二阶广义自治Birkhoff系统的全局稳定性.云南大学学报：自然科学版，2013，35（5）：638～643（Li Y M，Chen XW.Global stability of second order autonomous generalized Birkhoff system.Journal of Yunnan University：Natural Sciences，2013，35（5）：638～643（in Chinese））

8 Hirsch M W，Smale S，Devaney R L.Differential equations，dynamical systems，and an introduction to chaos.Singapore：Elsevier，2008

9 Mc Lachlan R I，Quispel G RW，Robidoux N.Geometric integration using discrete gradients.Philosophical Transactions of the Royal Society A，1999，357（1754）：1021～1045

10 梅凤翔.分析力学（下卷）.北京：北京理工大学出版社，2013（Mei F X.AnalyticalmechanicsⅡ.Beijing：Beijing Institute of Technology Press，2013（in Chinese））

11 Chen XW，Zhao G L，Mei FX.A fractional gradient representation of the Poincaréequations.Nonlinear Dynamics，2013，73（1-2）：579～582

12 梅凤翔.关于斜梯度系统.力学与实践，2013，35（5）：79～81（Mei F X.On the skew-gradient system.Mechanics in Engineering，2013，35（5）：79～81（in Chinese））

13 梅凤翔.广义Birkhoff系统动力学.北京：科学出版社，2013（Mei F X.Dynamics of generalized birkhoff system.Beijing：Science Press，2013（in Chinese））

14 马知恩，周义仓.常微分方程定性与稳定性方法.北京：科学出版社，2001（Ma Z E，Zhou Y C.Ordinary differential equation qualitative and stability theory.Beijing：Science Press，2001（in Chinese） ）

SINGULAR POINTS ANALYSIS FOR SECOND ORDER AUTONOMOUS GENERALIZED BIRKHOFF SYSTEMS*

Cao Qiupeng1Chen Xiangwei2†
（1.School of Mathematics and Physics，Suzhou University of Science and Technology，Suzhou215009，China）
（2.Department of Physics and Information Engineering，Shangqiu Normal University，Shangqiu476000，China）

The differential equations of the second order autonomous generalized Birkhoff systemswere firstly established.The linearized equations of this system were also given.The conditions for｀the translation of linearized system into a gradient system were put forward.The singular points for linearized system were analyzed by the characteristic of the gradient system.Moreover，the types of singular points for the corresponding nonlinear system were studied by Perron theorem.The results show that if the linearized system can be translated into a gradient system，the singular point for the corresponding nonlinear system is probably a node or a saddle point.

generalized Birkhoff system， gradient system， singular point

10.6052／1672-6553-2016-6

2015-9-10收到第1稿，2015-10-13收到修改稿.

*国家自然科学基金资助项目（11372169）和苏州科技学院研究生科研创新计划（SKCX14_056）

†通讯作者E-mail：hnchenxw＠163.com

Received 10 September 2015，revised 13 October 2015.

*This project is supported by the National Natural Science Foundation of China（11372169）and the Innovation Program for Scientific Research of Suzhou University of Science and Technology（SKCX14_056）

†Corresponding author E-mail：hnchenxw＠163.com