解题反思，提高数学解题能力的关键

覃泓钦

[摘 要]新的数学课程标准对学生的数学能力提出了新的要求，而数学能力的提高只有在学习和解决数学问题的过程中才能实现。因此我们在教学过程中，要培养学生对典型题型问题进行反思的习惯，认真反思，可以把解决问题的数学思想方法及对问题的再认识转化为一个学习过程，能提高学生分析和解决问题能力，从而使学生有信心有能力学好数学。

[关键词]解题反思；引导学生；数学思想方法；数学能力

对于提高数学解题能力，有诸多条件和因素。在实际中，许多初中学生完成作业，因为学习态度和心理状态的不同，或者老师缺少必要的指导和训练，大部分都缺少解题反思这一重要环节，未能形成良好的解题习惯，解题能力和思维品质未能在更深和更高层次得到有效提高和升华。为了提高同学的解题能力，应该倡导和训练学生进行有效的解题反思。反思是一个能动的、审慎的知识加工过程。初中生大多只是按部就班、照例模仿、套公式解题、重复机械按老师要求完成作业、应付考试，学生的解题只停留在解答结果的表层，而没有对题目涉及的概念、知识与能力进行回顾；也没有对解题方法与数学思想进行提炼与加工，更没有想到把本题的结论与数学思想进一步推广，而可以触类旁通。学生对解题的反思目的在于对学习进行诊断、纠错、创新，是一个吸取教训、总结方法、升华思想的过程，反思能让学生从“学会”变成“会学”。

一、反思解题思路，提高思维能力

解题本身不是学习的目的，而只是一种训练手段，学生在做题时应善于作解题后的反思，找出解题过程中所蕴含的概念、知识和能力，方法的归类、规律的小结和技巧的揣摩，再进一步作一题多变，一题多问，一题多解，挖掘例题的深度和广度，扩大例题的辐射面，无疑对能力的提高和思维的发展是大有卑益的。

例如：（原例题）已知等腰三角形的腰长是4，底长为6；求周长。我可以将原例题进行一题多变。

变式1：已知等腰三角形一腰长为7，周长为14，求底边长。（这是考查逆向思维能力）

变式2：已等腰三角形一边长为7，另一边长为6，求周长。（前两题相比，需要改变思维策略，进行分类讨论）

变式3：已知等腰三角形的一边长为3，另一边长为6，求周长。（显然“3只能为底”否则与三角形两边之和大于第三边相矛盾，这有利于培养学生思维严密性）

变式4：已知等腰三角形的腰长为X，求底边长y的取值范围。

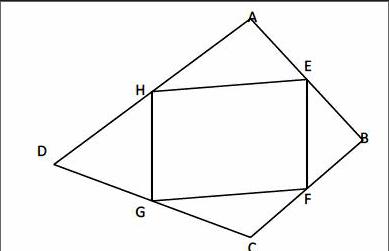
变式5：已知等腰三角形的腰长为x，底边长为y，周长是14。请先写出M者的函数关系式；再在平面直角坐标内画出M者的图象。（与前面相比，要求又提高了，特别是对条件0

通过例题的层层变式，学生对三边关系定理的认识又深了一步，有利于培养学生从特殊到一般，从具体到抽象地分析问题、解决问题；通过例题解法多变的教学则有利于帮助学生形成思维定势，而又打破思维定势；有利于培养思维的变通性和灵活性。

二、反思易错易漏，力求尽善尽美

学生的知识背景、思维方式、情感体验往往与成人不同，而且表达方式可能也不准确，又缺乏思维的严谨性，这就难免在解题过程中易错易漏，而只要学生能从此切入解题时进行反思，往往能找到“病根”，进而对症下药，常能收到事半功倍的效果。

初中学生刚学习有关有理数运算，对此下几个题目总是存在错误：

计算（-2）2，-22，-2-2，2-2，（-2）-2

反思为什么会有同样的错误，原因在于没有弄清各算式的意义，如：乘方的意义，负指数的意义，底数与幂的意义，甚至相反数的表示等，以及他们之间的联系，象-22与-2-2，2-2，要弄清底数是2，象（-2）2与（-2）-2底数是-2，当然在计算时也有小小的技巧，如负指数的计算，其实也可以，这样出错的概率就小。又如在讲同类项时，我提出：若单项式与是同类项。学生很快解出：得，“聪明”学生还会这样做：，得：，象如此频繁的错误，说明学生根本没去对出题者的意图进行反思，没有对基本概念进行反思；又如在几何题中经常会遇到根据位置或者形状不同而进行分类讨论的题目，学生也很容易造成疏漏，如：把一个矩形截去一个角，问还有几个角，学生回答是3个或许4个，其实答案是3个或4个或5个，如图：

像这样一个简单的问题，学生解题后也要去反思是否有疏漏或错误的地方，反思答案是否与题中隐含条件相抵触，是否有其它可能情况，是否掉入命题者所设的陷井，从而提高自己全面思考的能力，力求尽善尽美。

三、反思多向思维，以便触类旁通

一题多解是培养学生思维能力的一种有效手段，探讨解法多样性 ，是解题反思的重要内容，学生要学会对已知信息进行综合分析，探索其广阔外延，挖掘其深层信息，多角度切入问题，以不同的创新思维方式寻找新的思路和解法，达到举一反三，触类旁通。

四、反思思维迁移，享受成就感

学生做题往往是为做题而做题，没有认真分析解题后的知识的迁移，而学生在对题目进行反思引伸、拓展，会更进一步激发自身的求知欲望，培养自己自觉探究的良好习惯，享受成功的喜悦，培养学生创新思维能力。

例：已知四边形ABCD中，E、F、G、H分别是AB、BC、CD、DA的中点，求证：四边形EFGH是平行四边形。

学生对本题并不陌生，经过一翻思考，不难发现正确方法，但往往不去反思四边形的特殊性导致的结果，更没有从特殊迁移到一般的思维过程，学生在证明完成后可以反思：若四边形ABCD是特殊的四边形，如：矩形、菱形、正方形等时，四边形EFGH又是什么四边形呢？

得出结论后又进一步反思，此四边形若分别满足条件（1），对角线相等；（2）对角线相互垂直；（3）对角线相互垂直且相等；又是什么结果呢？

再反思：沿任意四边形对边中点剪开成4块，都可以拼成平行四边形（奇妙）。

通过这样的反思把结论从特殊到一般，而且使自己对特殊四边形的判定与性质及他们间的联系理解得更加透彻，达到对知识的迁移，并能得出如上奇妙而有趣的结果，享受了做数学题的成功。

学生解题反思，是学生提高数学能力的重要环节，引导学生不断对问题进行观察分析、归纳类比、抽象概括，对解题中所蕴含的数学方法、数学思想进行提炼与概括，重构自己的认知结构，从而发展思维、提高探索能力、引发再创造，是学生学好数学的关键。