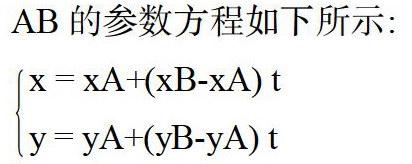基于钻孔数据地质信息的二维符号表达

孙艳君　王磊　钱冬梅

[摘要]论文针对地层生成、纹理填充和贝塞尔曲线的相关算法进行了研究，最后以天津天狮学院新校区的钻孔数据作为原始数据，采用VC++6.0作为开发平台，SQLServer作为后台数据库，结合MFC、STL和ADO等技术进行了验证，实现了地层的自动生成、点选、颜色和纹理填充、测井曲线等二维地质符号表达功能。

[关键词]钻孔；地层填充；贝塞尔曲线

1 引言

随着所探测地质信息的数据量变得越来越大，建立城市地质信息数据的综合管理系统，实现地质成果的数字化，可以为城市地质信息的科学有效的管理提供技术支撑，通过地质数据自动生成相关图形能够节省大量时间，同时相对于手工绘制具有更高的精度。

2 研究内容

系统针对多种图形生成算法进行了研究，本文的主要研究内容包括：（1）多边形任意点选算法；（2）多边形动态生成、颜色和纹理填充的算法研究；（3）贝塞尔曲线的研究和应用。

3 主要算法研究

3.1 点和多边形的点选

区域点选是通过判断各种图形元素是否与一个区域相交或包含在一个区域内来实现的。多边形点选包括矩形搜索法和多边形点选算法。

矩形搜索法是点选操作最常用的方法，根据当前点（x，y）生成搜索区域CRect rect（x-x0，y-y0，x+x0，y+y0），通过CRect类的PtInRect（CPoint pt）方法来判断点是否在CRect的区域内：多边形点选利用CRgn类的CreatePolygonRgn（）函数创建一个具有n个顶点的多边形区域，利用CRgn对象调用PtInRegion（CPoint pt）函数判断点是否在区域内。

3.2 地层生成算法

通过点选或画线的方式在钻孔平面分布图上选择一个或多个钻孔，实现钻孔地层的自动生成。假设同一个钻孔的每一层处在同一水平面上，采用二维Vector结构存储钻孔的地层厚度、深度和地层编号，经过分析相邻钻孔之间地层的关系，地层生成可分为六种情况。

（1）选中钻孔坐标、钻孔编号和地层起点的坐标；假设i代表当前钻孔的编号，j代表第i个钻孔的地层编号，k代表第i+1个钻孔的地层编号。

（2）若i<钻孔数，i++，j=0，k=0，转（3）；否则转（10）。

（3）若i<最后一个钻孔，则根据该钻孔的地层编号和系统窗口右边界x的坐标值right x绘制该钻孔的地层，转（10）；否则转（4）。

（4）若j<第i个钻孔的地层数，k<第i+1个钻孔的地层数，转（5）；否则转（2）。

（5）若第i个和第i+1个钻孔所对应的地层编号相等，则直接连接相应的地层；记录该地层多边形并用颜色填充；j++，k++，转（4）；否则转（6）。

（6）若第i个钻孔的地层编号<第i+1个钻孔所对应的地层编号，则将第i个钻孔的地层编号j与第i+1个的钻孔的k-1个地层相连：记录该地层多边形并用颜色填充；j++；转（4）；否则转（7）。

（7）若第i个钻孔的地层编号>第i+1个钻孔所对应的地层编号，则将第i个钻孔的j-1个地层与第i+1个的钻孔的k个地层相连，记录该地层多边形并用颜色填充，k++，转（4）；否则转（8）。

（8）若第i个钻孔的地层i还有剩余，则将第i个钻孔的剩余地层都与第i+1个钻孔的最后一个地层相连：记录该地层多边形并用颜色填充，j++，转（4）；否则转（9）。

（9）若第i+1个钻孔的地层k还有剩余，则将第i+1个钻孔的剩余地层都与第i个钻孔的最后一个地层相连；记录该地层多边形并用颜色填充，k++，转（2）。

（10）结束。

3.3 地层颜色填充算法

通过分析。地层生成算法所绘制的地层包括三角形和四边形。因为三角形和四边形的填充方法不一样，所以在生成地层的同时，判断当前的地层属于哪一种情况，然后利用CDC类的成员函数实现地层颜色动态填充。设m_ZbPol是存储地层多边形的数组。根据m_ZbPol中的每一个多边形的点数调用Polyline方法来建立多边形曲线，调用FillPath方法和相应地层的颜色进行填充。

主要的实现代码如下：

pDC->BeginPath（）；//路径开始

pDC->Polyline（m ZbPol，n）；//m_ZbPol为CPiont类型的数组，n为数组个数

pDC->EndPathO；//确定填充的路径

pDC->SelectObject（CreateSolidBrush（RGB（255，0，0）））；

pDC->FillPath（）；//填充一个地层多边形。

3.4 地层纹理填充算法

为了使地层看起来更加真实，可以为地层添加相应的纹理，纹理在程序设计中可理解为位图。常用的位图填充方法是扫描线法，需要确定、交点位置和边界处理几个问题。

3.4.1 交点位置的处理

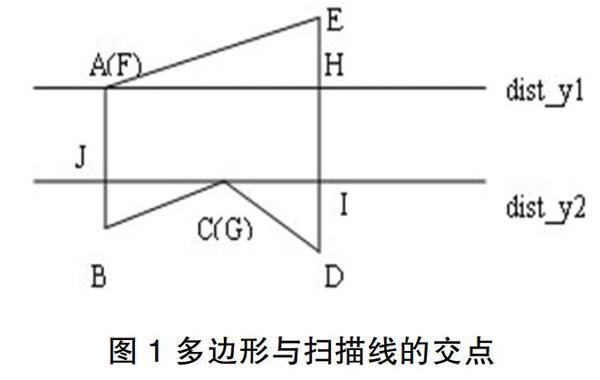
扫描线与多边形的顶点相交包括两种情况：当顶点相邻的两条边落在顶点的异侧时，交点计1个，如图1中A（F）点；当顶点相邻的两条边落在顶点的同侧时，交点计0个或2个，如图1中C（G）点。处理过程为对于每一条扫描线，判断交点中是否有相等的点，若存在相等点，判断属于同侧相交还是异侧相交，主要通过交点和直线两点的横坐标进行比较进行判定，然后再分别处理。

3.4.2 边界区域的位图填充处理

本系统采用的位图格式为2n*2n，在确定了位图的位置后，并不能直接显示，因为确定的位置是一个点，而位图有一定的高和宽，在多边形边界附近的位置上显示位图时，位图的一部分有可能在区域外。

3.4.3 判断直线与矩形是否相交

位图与多边形边界的相交可以理解为直线（多边形的边）与矩形（位图）的相交。判断直线与矩形域是否相交可以利用直线段与直线段的求交算法。如图2所示，设AB为多边形区域某一条边，CD是位图区域的某一边界。

AB的参数方程如下所示：CD的参数方程如下所示：

从中解出s，t，如果1≥s，t≥0，则两直线段相交。同理可得出AB与其他三条边界的相交的条件。

3.4.4 直线段与矩形求交点算法

利用直线段与矩形求交点运算来判断位图的边和多边形是否相交。确定位图的左上角坐标和右下角坐标，针对位图的每条边都遍历当前多边形的所有边，若存在相交情况，终止判断并且不显示位图；若不存在相交的情况，则显示位图。

3.4.5 位图填充算法

对于每一条扫描线，其具体实现步骤如图3所示。

3.5 贝塞尔曲线

贝塞尔曲线是应用于二维图形的数学光滑曲线，包括线性、二次方和三次方贝塞尔曲线。三次贝塞尔曲线具有中间点较少和效果好的优点，被广泛地应用在计算机图形中用于平滑曲线建立模型。P0、P1、P2、P3四个点在平面或在三维空间中定义了三次方贝塞尔曲线。曲线起始于P0，按照P0、P1、P2、P3的顺序结合参数的变化走到P3。

曲线的参数形式如下所示：

B（t）=（1-t）³P₀+3t（1-t）²P₁+3t²（1-t）P₂+t³P₃t∈[0，1]。

贝塞尔曲线三次贝塞尔曲线的基本结构如图4所示：建构高阶曲线，需要相应的中介点。对于三次曲线，便需要相应更多的中介点，可由线性贝塞尔曲线描述的中介点Qo、Q1、Q2，和由二次曲线描述的点R0、R1所建构。

测井曲线是利用测井所得到的岩层的物理特性所绘制出来的反应地层物理特性变化趋势的曲线。利用贝塞尔曲线绘制光滑曲线时，完成一次绘图都至少需要四个点，所以平滑点的个数必须满足nCount%3=1。前一次绘图的最后一个点是下一次绘图的起点，即平滑点的个数为4+3^*n（n=0，1，2……）。若是点数不满足上述条件。则将源点集的最后一个点重复加入，直到满足条件为止（至多加入两次），这样既完成了绘图又不会造成太大的偏差。这种解决方法也用于二维地形剖面图中地形剖面图的平滑。

4 实例验证及结论

以天津天狮学院新校区的钻孔数据作为研究对象，采用VC++600作为开发平台，SQLServer建立系统数据库，结合ADO、STL和多种算法实现了二维钻孔点选、任意钻孔的地层分布图、地层颜色及纹的填充、测井曲线的加载。岩层有多种物理特性，本实验选取了含水量（Wo，%）、孔隙度（n，%）、压缩模量（Es，MPa）、直快粘聚力（C，KPa）和直快摩擦角（φ，°）五个物理特性分别反应了土的含水量、密度、压缩性和抗剪性。由于测井信息量不足，采用取平均值的方式表示同一地层各种物理特性的值，但不会改变物理特性曲线的总体变化趋势。最终的效果如图5所示。

系统通过Vc++6.0平台和数据库技术，将系统的相关技术和算法用于天津天狮学院新校区的钻孔数据中，验证了相关理论，并实现了地质信息的符号表达及可视化，为三维地质建模奠定了基础。