一道数学竞赛题的五种解法及一般形式

孙 倩（安徽大学数学科学学院，合肥230601）



一道数学竞赛题的五种解法及一般形式

孙 倩
（安徽大学数学科学学院，合肥230601）

［摘 要］给出第十届江苏省大学生数学竞赛一道试题的五种解法并对试题作出推广．

［关键词］数学竞赛；一题多解；级数；比值判别法；推广

第十届（2012年）江苏省大学生数学竞赛本科一级竞赛题的第七题为

已知数列

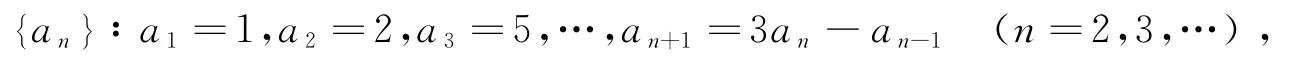
该试题的参考答案如下：

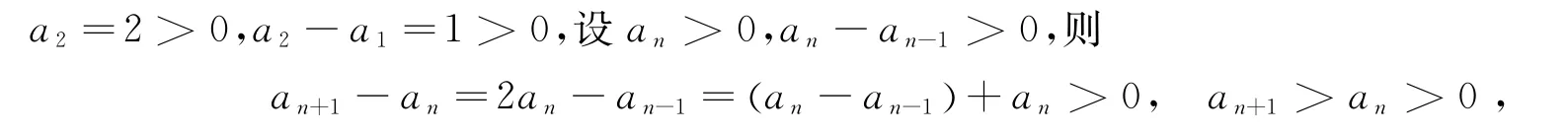
除上面解法之外，本文再给出该试题的其他四种解法并给出该试题的推广，亦即它的一般形式．

解法一 利用正项级数敛散性的比值判别法．

由题设知

从而有

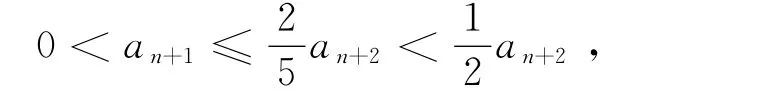
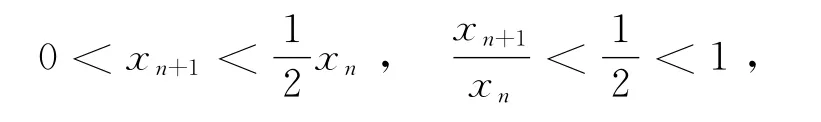
注 也可由

解法二 利用正项级数收敛的充要条件

解法三 通过解二阶差分方程求出｛an｝的通项，进而判别的敛散性．

因为数列｛an｝满足二阶常系数齐次差分方程an＋1－3an＋an－1＝0，此差分方程对应的特征方程为λ2－3λ＋1＝0，解得其特征根，故

其中c1，c2为待定常数．

由a1＝1，a2＝2知

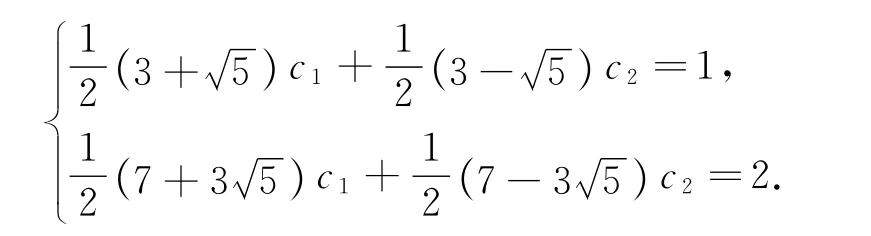
由｛an｝的通项公式知an＞0（n＝1，2，…），从而

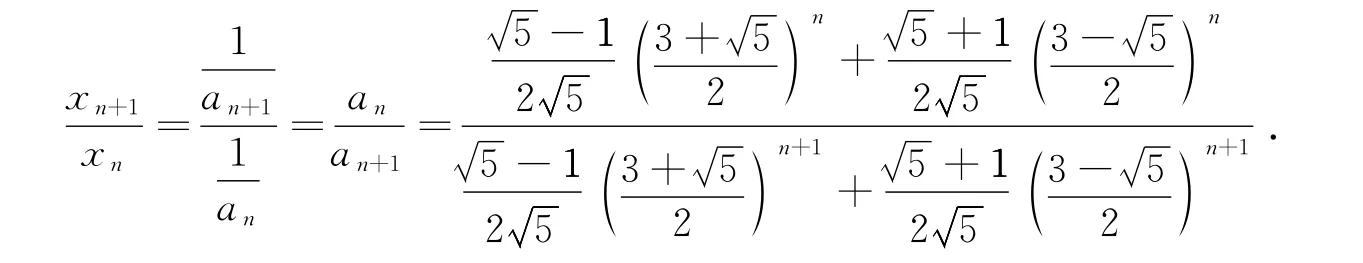
解法四 利用矩阵方法求出｛an｝的通项，进而判别的敛散性．

由题设an＋1＝3an－an－1知

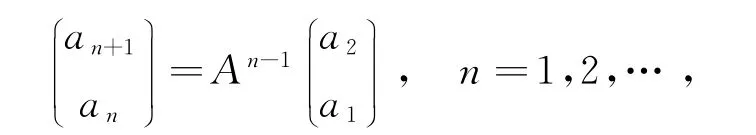
矩阵A的特征方程为

于是

因此

所以

上式右端分子、分母同除以λn－11，注意到，则有，由正项级数敛散性的比值判别法的极限形式知级数收敛，即绝对收敛，从而收敛．

下面给出本文所讨论试题的一般形式及相关结论．

设数列｛an｝满足

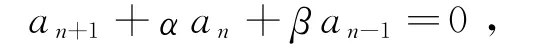
其中α，β为实常数且a1，a2为已知（n＝2，3，…）．若方程λ2＋αλ＋β＝0存在实根λ1，λ2，且，则级数收敛．

证 因为二阶线性齐次差分方程

的特征方程λ2＋αλ＋β＝0的两个实根分别为λ1，λ2（不妨设所以

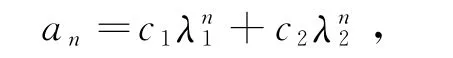
其中c1，c2为待定常数（由a1，a2定出），于是

上式右边分子、分母同时除以λn1，注意到令n→∞，由于，所以

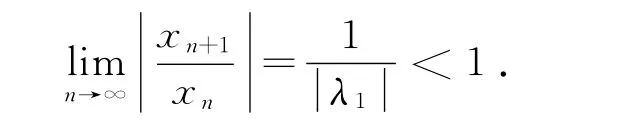
［参 考 文 献］

［1］ 同济大学数学系．高等数学（下册）［M］．6版．北京：高等教育出版社，2012．

Five Solutions and General Form to one Mathematics Contest

SUNQian
（School of Mathematics，Anhui University，Hefei 230601，China）

Abstract：This paper presents five methods of solving the questions of tenth college students’mathematics contest in Jiangsu province，and makes a promotion to the question．

Key words：mathematics contest；multi－answer question；series；ration discrimination method；spread

［收稿日期］2015－11－15

［中图分类号］O173．1

［文献标识码］C

［文章编号］1672－1454（2016）01－0114－04