基于曲线导数的二元函数微分中值定理

朱 灿， 洪 丹（上海理工大学理学院，上海200093）



基于曲线导数的二元函数微分中值定理

朱 灿， 洪 丹
（上海理工大学理学院，上海200093）

［摘 要］给定二元函数，文献［1］定义了其在光滑曲线上的方向导数（简称为曲线导数）．本文主要利用曲线导数建立二元函数的微分中值定理，比如罗尔定理，拉格朗日中值定理，柯西中值定理．这些中值定理可视作一元函数微分中值定理在二维情形的推广．

［关键词］曲线导数；罗尔定理；拉格朗日中值定理；柯西中值定理

1　引 言

一元函数微分学是研究度量空间（ℝ，d）或其子空间上函数的分析性质．距离d是建立极限理论的前提，而一元函数微分学的基本工具是极限．传统上，二元函数微分学采取了另外的办法，即从偏导数的角度来建立微分学理论．但二者存在明显的区别．例如，一元函数的可微性和可导性等价，但二元函数的偏导数存在性无法刻画可微性．甚至在现在通用的数学分析教材［2－4］中都没有给出二元函数可微性的等价条件．文献［1］中提出了二元函数的曲线导数的概念，并且证明了可微性和曲线导数存在等价．本文试图用曲线导数来建立二元函数的微分中值定理．

2　曲线导数

定义［1］二元函数z＝f（x，y）在点P0的某邻域内有定义．设l是以P0为起点的光滑曲线，点P

为曲线l上任一点，P0到P的沿曲线l的弧长为．若极限

存在且有限，则称此极限为函数f（x，y）在点P0处沿曲线l的导数，简称为曲线导数，记作f′l（P0）或，其中指点P沿曲线l无限趋近于P0．

定理［1］函数z＝f（x，y）在点P0可微的充要条件是函数z＝f（x，y）在点P0处沿任意光滑曲线l上的曲线导数均存在且

该定理解决了当函数的偏导数在某一点不连续时，函数仍在这一点处可微的问题，弥补了用偏导数连续来判别可微性的不足，从而丰富了多元函数可微性的判别理论．考虑以下例子．

例 讨论二元函数

在点（0，0）处的可微性．

由可微的定义易知该函数在点（0，0）处可微，但偏导数f′x（x，y）与f′y（x，y）在点（0，0）处不连续．由曲线导数定义，函数f（x，y）沿任意一条过点（0，0）的光滑曲线l的曲线导数均存在且

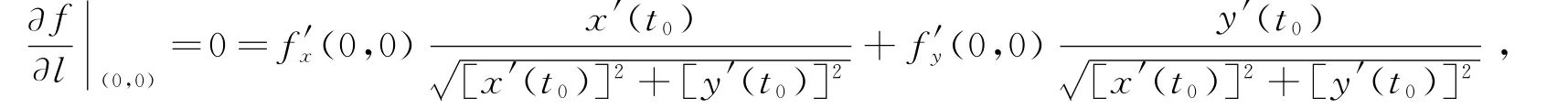
从而函数f（x，y）在点（0，0）处可微．更多的例子请见参考文献［1］．

3　中值定理

有了曲线导数的定义后，虽然曲线导数已经被用来刻画可微性，但现存文献中并没有关于曲线导数的运用．所以本节主要将一元微分中值定理推广至基于曲线导数的多元函数的微分中值定理，如罗尔中值定理，拉格朗日中值定理，柯西中值定理等．

3．1 费马定理

定理1（费马引理） 设函数z＝f（x，y）是在点P0（x0，y0）的某邻域内有定义的二元函数，且在点P0处可微．如果点P0是函数f（x，y）的极值点，则函数z＝f（x，y）在点P0的沿任意光滑曲线l的曲线导数存在且皆为零．

而函数z＝f（x，y）在点P0处可微，并且点P0是f（x，y）的极值点，那么

从而函数z＝f（x，y）在点P0（x0，y0）的沿任意曲线l的曲线导数皆为零．

3．2 罗尔中值定理与拉格朗日中值定理

证 若函数z＝f（x，y）在D上连续，则在任一光滑曲线l上函数

（记作z＝g（t））有最大值和最小值，分别用M与m来表示．以下分为两种情况讨论：

①当M＝m时，则函数z｜l＝f（x，y）｜l必为常数，记作f（x，y）｜l＝C，其中C为常数．由曲线导数定义可知，任意点Pξ处沿曲线l的曲线导数皆为零．即结论成立．

②当M＞m时，由于f（x0，y0）＝f（x1，y1），那么最大值M与最小值m至少有一个不在点P0和P1处取得，即为函数z＝g（t）的极值点．由条件（i），f（x，y）在D上可微，则函数z＝g（t）可微．由一元函数的费马引理，存在ξ使得g′（ξ）＝0．设ξ对应的点为Pξ（x（ξ），y（ξ））．因为

（i）z＝f（x，y）在D上可微； （ii）f（x0，y0）＝f（x1，y1），则在曲线l上至少存在一点Pξ（x（ξ），y（ξ）），使得

证 作辅助函数

易知函数F（x，y）在有界闭区域D上可微，且有F（x0，y0）＝F（x1，y1）＝0．由罗尔定理可知，则在曲线l上至少存在一点Pξ（x（ξ），y（ξ）），使得．而函数F（x，y）在点Pξ（x（ξ），y（ξ））处的沿曲线l的曲线导数为

而由F（x，y）的构造知

由定理中曲线导数的计算公式可得等式

3．3 柯西中值定理

定理4（柯西中值定理） 设D⊂ℝ2是有界闭区域且点P0（x0，y0），P1（x1，y1）∈D．设l是以P0为起点，P1为终点的任一光滑曲线且其参数方程为．设函数z＝f（x，y），w＝g（x，y）是

（iii）g（x0，y0）≠g（x1，y1），

则在曲线l上至少存在一点Pξ（x（ξ），y（ξ）），使得在区域D内有定义的二元函数．若函数z＝f（x，y）与w＝g（x，y）满足如下条件：

（i）z＝f（x，y）与w＝g（x，y）在D上可微；

（ii）曲线导数

所以函数F（x，y）在有界闭区域上D可微，且有F（x0，y0）＝F（x1，y1）＝0．由罗尔定理可知，则在曲线l上至少存在一点Pξ（x（ξ），y（ξ）），使得

证 作辅助函数．而函数F（x，y）在点Pξ（x（ξ），y（ξ））处沿曲线l的曲线导数为

因为

所以有））

由定理中曲线导数的计算公式可得

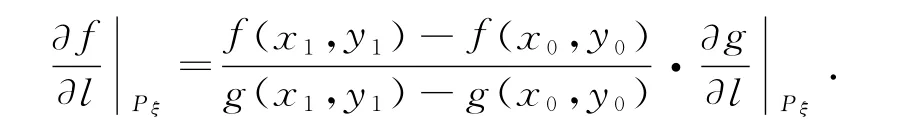
4　结 论

本文讨论了基于曲线导数的二元函数的微分学中值定理，得到了完全类似于一元函数的微分中值定理．更进一步，还可以在此基础上讨论高阶曲线导数及二元函数的泰勒定理，限于篇幅关系未作展开．

［参 考 文 献］

［1］ 舒世昌．多元函数的曲线导数与可微［J］．咸阳师专学报，1994，9（6）：3－6．

［2］ 华东师范大学数学系．数学分析下册（第四版）［M］．北京：高等教育出版社，2011．

［3］ 张筑生．数学分析新讲（共三册）［M］．北京：北京大学出版社，1990．

［4］ 菲赫金哥尔茨．微积分学教程［M］．北京：高等教育出版社，1957．

Differential Mean Value Theorems Based on the Curve Derivative of Binary Function

ZHU Can， HONG Dan
（College of Science，University of Shanghai for Science and Technology，Shanghai 200093，China）

Abstract：For a given binary function，its’directional derivative on a smooth curve is defined in reference(［1］)（often called curve derivative briefly）．Some differential mean value theorems of binary function are studied based on The Curve Derivative，such as Rolle theorem，Lagrange mean value theorem and Cauchy mean value theorem．These differential mean value theorems can be viewed as a generalization of the one of one variable function．

Key words：curve derivative；Rolle theorem；Lagrange mean value theorem；Cauchy mean value theorem

［基金项目］沪江基金（B14005）

［收稿日期］2015－07－25

［中图分类号］O172．1

［文献标识码］C

［文章编号］1672－1454（2016）01－0110－04