两个极限相等的有趣数列

杨天虎， 岳志明（酒泉职业技术学院，甘肃酒泉735000）



两个极限相等的有趣数列

杨天虎， 岳志明
（酒泉职业技术学院，甘肃酒泉735000）

［摘 要］证明了两个有趣数列的极限均为且

［关键词］沃利斯公式；单调数列；数列极限

本文讨论的两个极限相等的有趣数列的性质可归纳为以下定理．

证明如下．

1　预备知识

公式

沃利斯（Wallis）公式［1］

2　构造数列

设有数列

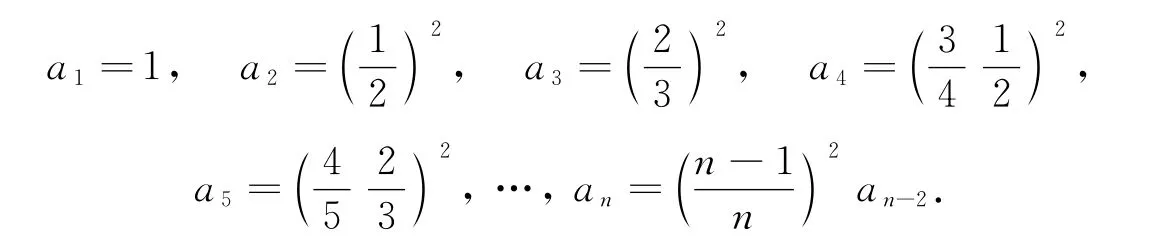
将数列｛an｝分为｛a′n｝，｛a″n｝两个数列，即

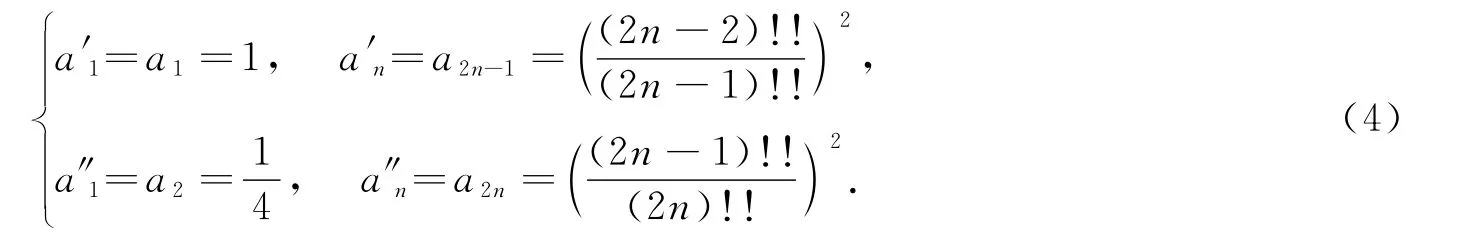
｛an｝的通项公式为

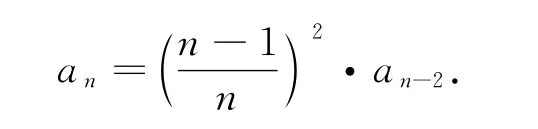
即数列｛a′n｝，｛a″n｝均为大于0的严格单调减小数列．

设有数列｛bn＝n an｝，将数列｛bn｝也分为｛b′n｝，｛b″n｝两个数列，即

因

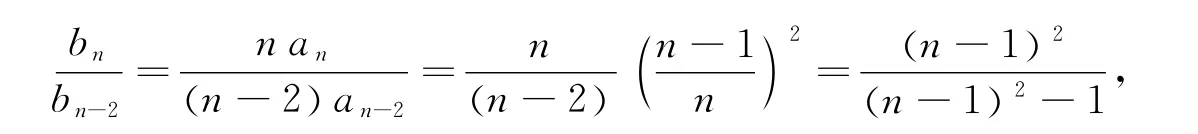
所以｛bn｝的通项公式为

即数列｛b′n｝，｛b″n｝均为严格单调增加数列．

设有数列｛cn＝（n＋1）an｝，将数列｛cn｝也分为｛c′n｝，｛c″n｝两个数列，即

因

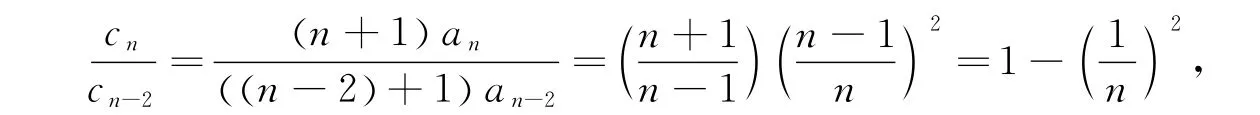
所以｛cn｝的通项公式为

即数列｛c′n｝，｛c″n｝均为大于0的严格单调减小数列．且存在

3　求数列极限

第一种情况，求数列｛a′n｝，｛b′n｝，｛c′n｝的极限．

因｛a′n｝，｛c′n｝是均为大于0的严格单调减小数列，所以数列｛a′n｝，｛c′n｝均存在极限，因此

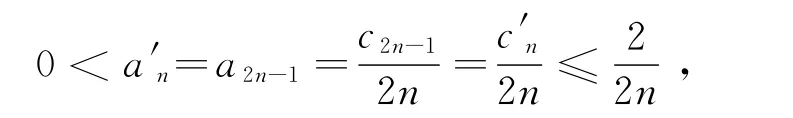
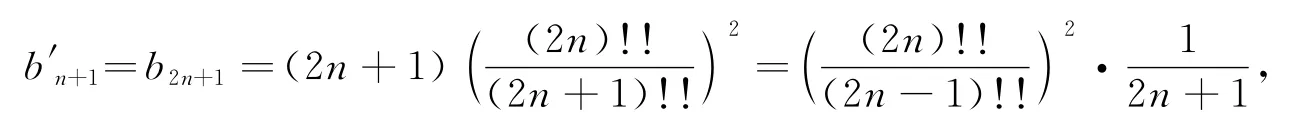
由（3），（7）式得

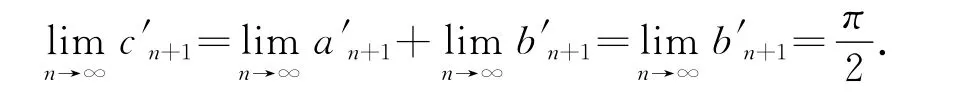
根据（2），（5），（6）式得

π

所以，｛y′n＝y2n－1｝为严格单调增加数列，｛z′n＝z2n－1｝为严格单调减小数列，

定理的结论（1）得证．

第二种情况，求数列｛a″n｝，｛b″n｝，｛c″n｝的极限．

因｛a″n｝，｛c″n｝也是均为大于0的严格单调减小数列，所以数列｛a″n｝，｛c″n｝均存在极限，同样可得由（6）式得

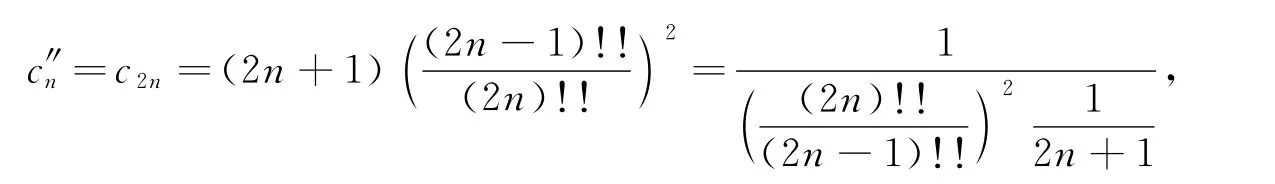
由（3），（7）式得

根据（1），（5），（6）式得

所以，｛y″n＝y2n｝为严格单调增加数列，｛z″n＝z2n｝为严格单调减小数列，

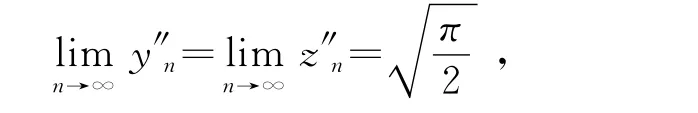
定理的结论（2）得证．

综合（8），（9）式，及定理的（1），（2）结论，可得

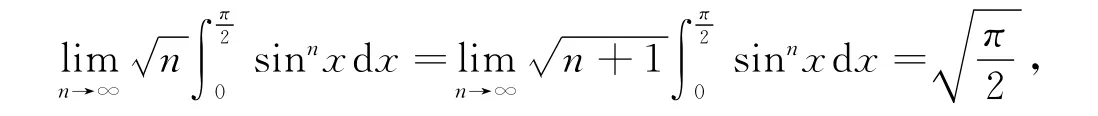
且

定理的结论（iii）得证．

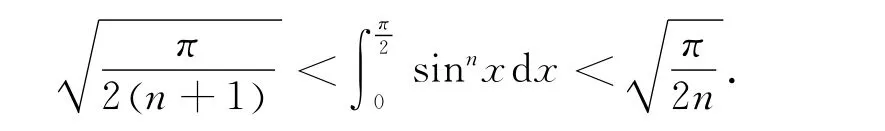
4　结束语

调减小数列，对数列｛yn｝，｛zn｝各取前20项数据计算验证，猜想得到了证实，但无法证明．

［参 考 文 献］

［1］ 华东师范大学数学系．数学分析（上）（第三版）［M］，北京：高等教育出版社．2001：226－227．

Two Interesting Sequences Having Equal Limit

YANG Tian－hu YUE Zhi－ming
（Jiuquan Vocational and Technical College，Gansu Jiuquan 735000，China）

Abstract：It is proved that the limit of the two Interesting Sequencesand

Key words：Wallis formula；monotone sequences；limit of a sequence

［基金项目］甘肃省科技计划资助（1309RTSF043）；甘肃省科技创新平台专项资助（144JTCF256）

［收稿日期］2015－04－30

［中图分类号］O178

［文献标识码］C

［文章编号］1672－1454（2016）01－0101－04