高等数学一题多解样例教学中的变式思维
董锦华,耿秀荣(桂林航天工业学院理学部,广西桂林541004)
高等数学一题多解样例教学中的变式思维
董锦华,耿秀荣
(桂林航天工业学院理学部,广西桂林541004)
摘要:运用样例进行解题教学,会时常用到解题变式。其中的一题多解能够充分体现变式思维。运用不同数学分支中的方法、运用在同一数学分支中不同的数学原理、运用同一数学原理的不同时机与角度,都能解决同一个数学问题。因此,在高等数学一题多解样例教学中,应该注重培养学生的变式思维能力。
关键词:高等数学;一题多解;样例;变式思维
1 引言
样例,即例子或范例,是一种能够阐释概念原理、展现事物性质的实体或样本,它值得模仿或推广。[1]在高等数学教学过程中具有重要作用。
作为一种思维方法,变式思维能够帮助学习者建立新知识与原有知识的桥梁,从而降低认知负荷。因此,在高等数学教学中具有重要意义。
解题变式常用于以样例为教学手段的解题教学。它主要包括一题多解、一题多变和多题归一。三者从不同侧面观照题目,进而揭示其本质和特征。[2]然而,限于篇幅,本文只研究高等数学一题多解样例教学中的变式思维。
2 高等数学一题多解样例教学中变式思维的体现
为了深入研究高等数学一题多解样例教学中蕴含的变式思维,我们从以下三个角度入手:运用不同数学分支中的方法解决同一个问题、运用在同一数学分支中不同的数学原理解决同一个问题、运用同一数学原理的不同时机与角度解决同一个问题。
2.1 运用不同数学分支中的方法解决同一个问题
采用高等数学不同分支中的方法解决同一个问题,是一题多解中常用的方法。下面,我们举一个既可以用代数法解决,也可以用几何法解决的样例。
例1.求
解法1:(代数法)令x=Rcost(0 则原式= 解法1的思路为:既然被积函数是根式,那么就需要设法去掉根号,因而可以采用三角代换办法。 解法2:(几何法) 可见本题既可以用代数法,又可以用几何法。这就体现了变式思维。运用变式思维,采用不同数学分支中的方法,从不同角度观察、解决同一问题,有利于拓展思路、培养发散思维能力和创新意识。 2.2 运用在同一数学分支中不同的数学原理解决同一个问题 在高等数学的同一数学分支中,有着很多不同的数学原理。如果具有变式思维能力,学习者就易于想到灵活运用这些原理解决同一问题。 解法1. 解法1的难点是三角函数的和差化积公式。如果对这些公式记忆不牢,就不容易想到运用它们。因此,这类问题难以解决。 好在我们可以运用变式思维,用同一数学分支中的不同数学原理解决同一问题。就型的未定式,我们完全可以运用洛必达法则,而不需要运用三角函数的和差化积公式。于是,出现下列解法: 在该解法中,通过两次运用洛必达法则,我们直接把原问题转化为一个简单的求极限问题。事实上,我们还可通过运用泰勒公式对余弦函数进行处理的方式得到更为简便的解法: 在该解法中,我们运用泰勒公式把函数,然后,利用连续函数的积分上限函数的可导性质,得到本题的新解法: 解法4 以上四种解法告诉我们,同一个问题可以用同一数学分支中的不同数学原理进行解决。 2.3 运用同一数学原理的不同时机与角度解决同一个问题 有时候,在不同时机、从不同角度运用同一个数学原理,会带来不同的解法。 2.3.1在不同时机运用同一数学原理 例3 求极限 运用第二个重要极限公式,就要对原题的函数进行改造,转化为的形式。其中里的表达式是根据需要硬凑出来的,而具体凑成“()”的时机不同,因此,我们至少可以得到以下两种解法: 解法1: 2.3.2 从不同角度运用同一数学原理 从不同角度运用同一数学原理,也可以得到多种解法。 在拆项的过程中,解法1和解法2都能产生的弧长。 如果利用《高等数学》第266页积分表中的第39个积分公式[]3: 我们可以得到如下解法: 结合曲线的对称性,得到曲线的弧长: 如果利用《高等数学》[]3第269页积分表中的第79个积分公式 则出现如下解法: 解法2:由曲线的方程,得 利用曲线的对称性,得到曲线的弧长: 解法3:令y=tant,原式可化为 我们还可以通过换元,把[0,2]的定积分化成无穷积分,再利用分部积分与常用积分进行求解,于是得到如下解法: 解法4:由曲线的方程,得 结合曲线的对称性,得到曲线的弧长: 于是 从不同角度运用同一数学原理,将会产生不同的技巧和解法。 考虑三函数之间的相互关系,运用变式思维,可以运用不同的转化技巧,可以得到不同的解法。 综上所述,高等数学一题多解样例教学中的变式思维有许多表现方式。无论是运用不同数学分支中的方法解决同一个问题,运用在同一数学分支中不同的数学原理解决同一个问题,还是运用同一数学原理的不同时机、不同角度解决同一个问题,都能够让我们感受到变式思维的存在及其重要性。 在高等数学一题多解的样例教学中,变式思维发挥着巨大作用。因此,我们要善于运用变式思维,从不同侧面入手,找到数学问题变化过程中的“不变”,然后,以此为切入点,找到解决问题的不同方法。 参考文献: [1]邵光华.数学样例学习的理论与实证研究[D].华东师范大学博士学位论文,2003. [2]耿秀荣.“几何画板”在数学解题变式中的应用和体现[J].铜仁学院学报,2011(1):141-144. [3]黄立宏.高等数学(上,第四版)[M].上海:复旦大学出版社,2014:6. (责编:彭麟淋责校:明茂修) The Variant Thinking during Exam ple Teaching ofM ulti-solution Questions in Higher M athematics DONG Jin-hua,GENGXiu-rong Abstract:Examplesare used to teach studentshow to solve the problem,which uses the variantsofsolv⁃ing the problems.As one of the variants,multi-solution questions can fully reflect the variant thinking.The samemathematicalproblems can be solved usingmethodsofdifferentmathematicalbranches,differentprinci⁃ples of the samemathematical branch,differentopportunities and angles of the samemathematical principle.Therefore,during example teaching ofmulti-solution questions in highermathematics,we should pay atten⁃tion to the students'ability of the variant thinking. Key words:HigherMathematics;Multi-solution Questions;Sample;Variable Thinking 作者简介:董锦华(1961-),男,广西贺州人,桂林航天工业学院理学部教授。研究方向:数学课程与教学论、微分方程。 基金项目:桂林航天工业学院基金项目“本科合格课程建设研究”,项目编号:2013HGKC02。 收稿日期:2015-10-23 中图分类号:O1 文献标识码:A 文章编号:2096-0239(2016)01-0132-07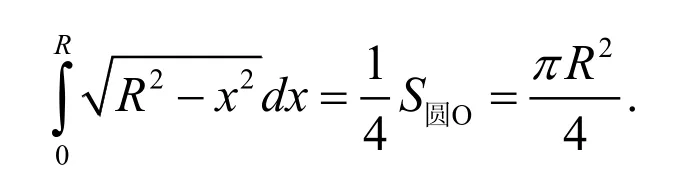
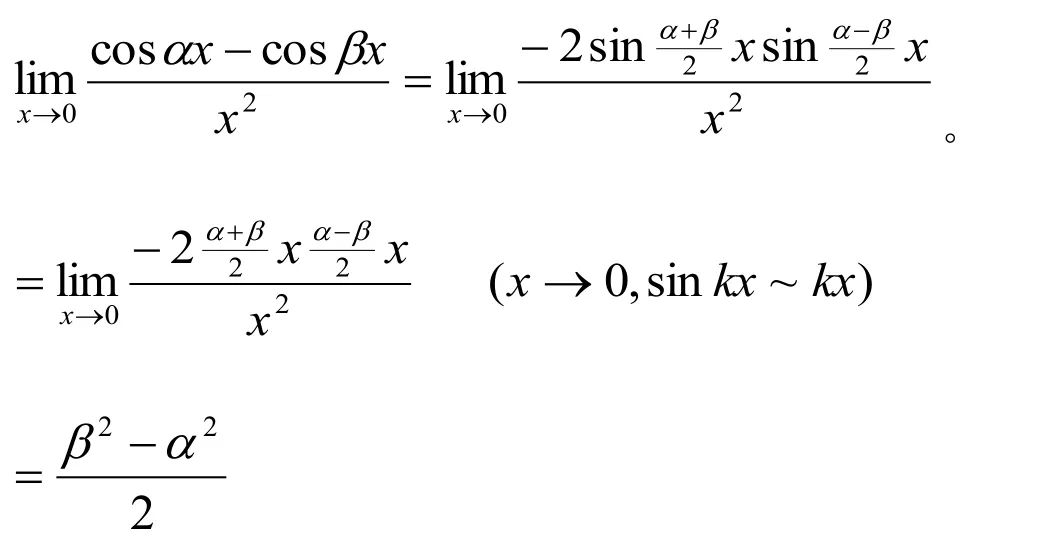
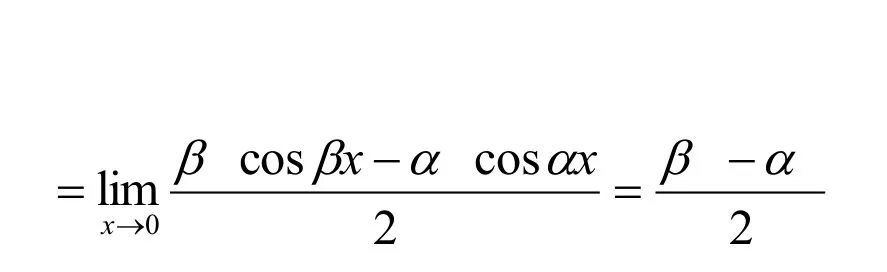
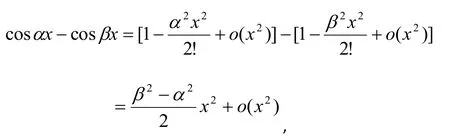
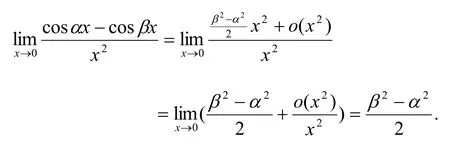

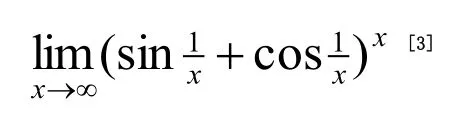
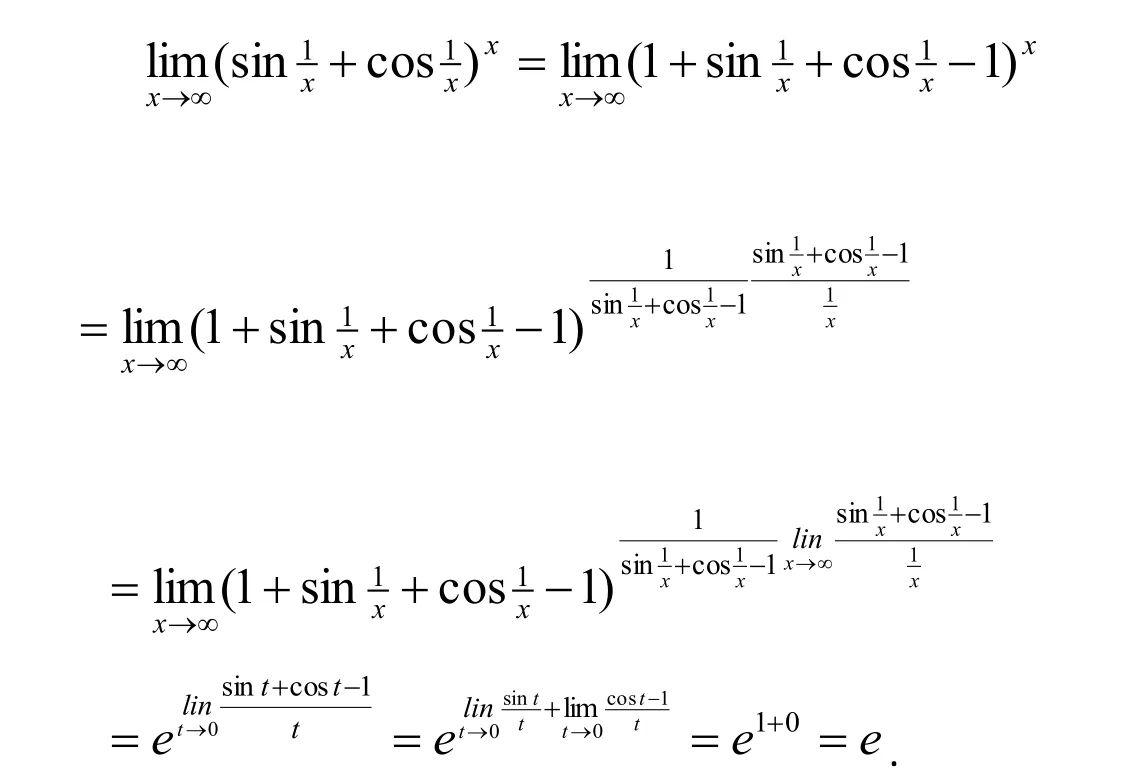
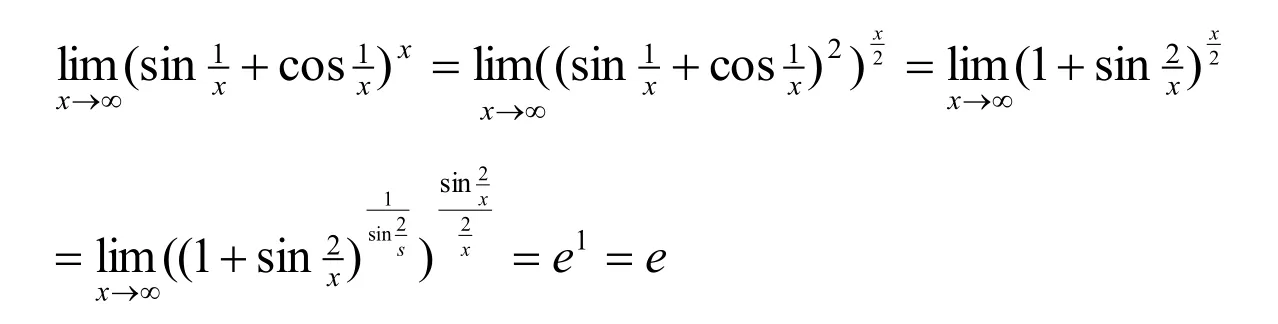
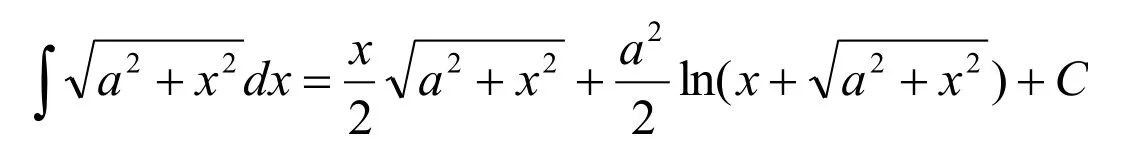
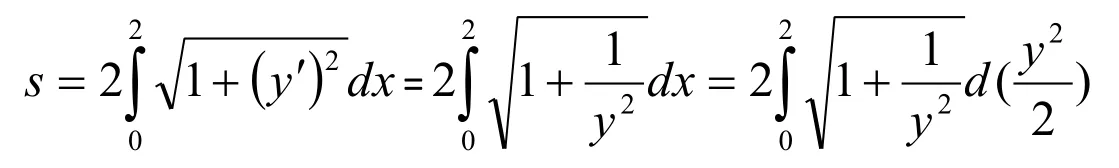
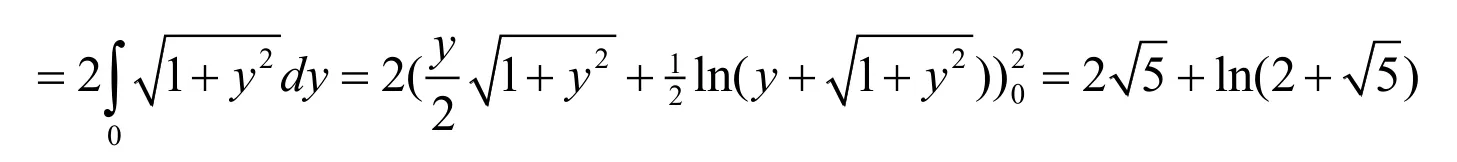
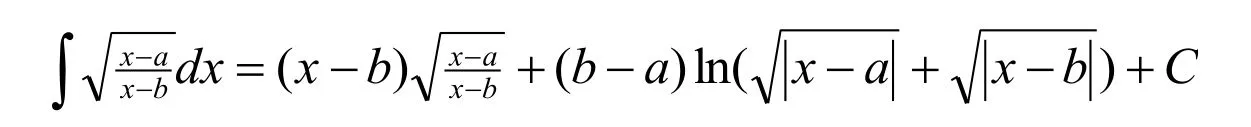
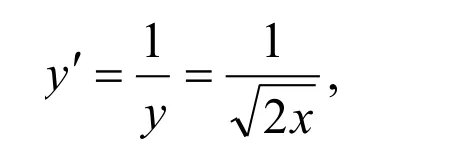
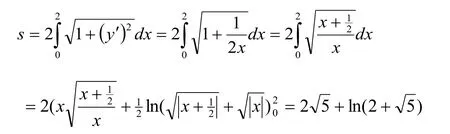

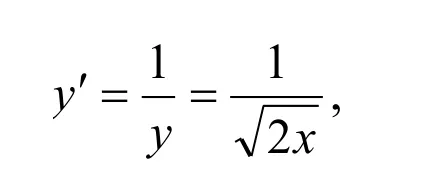
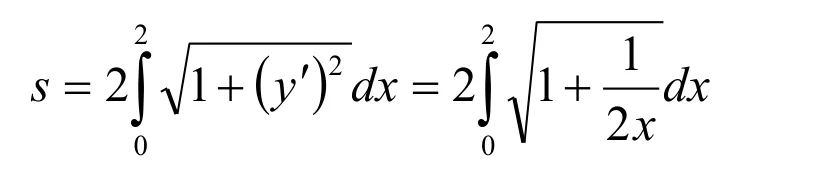
3结语
(Faculty ofScience atGuilin University of Aerospace Technology,Guilin,Guangxi541004,China)

