一类复高阶非线性代数微分方程解的研究
金 瑾,黄 雕(.贵州工程应用技术学院理学院、循环经济研究院,贵州毕节55700;.贵州民族大学理学院,贵州贵阳55005)
一类复高阶非线性代数微分方程解的研究
金瑾1,黄雕2
(1.贵州工程应用技术学院理学院、循环经济研究院,贵州毕节551700;2.贵州民族大学理学院,贵州贵阳550025)
摘要:利用亚纯函数的Nevanlinna值分布理论,研究一类复代数微分方程的亚纯解的问题,得到一个结论,推广和改进了高凌云等人的结论。
关键词:代数微分方程;亚纯解;代数体函数;值分布理论
1 引言及主要结果
假设读者熟悉Nevanl inna值分布理论的通常记号[1-11]。
关于微分方程的解问题,很多作者做了大量的工作,得到了一些结果(1-19)。
1983年N.Toda考虑了如下方程

得到结果如下:
定理A[1]当微分方程(1.1)不存在允许解,除了n-m是n的因子以及(1.1)有形式以外,其中a是一个常数.
2004年,高凌云又研究了具有允许解的代数微分方程组的形式,得到如下结论:
定理D[2]设复代数微分方程组


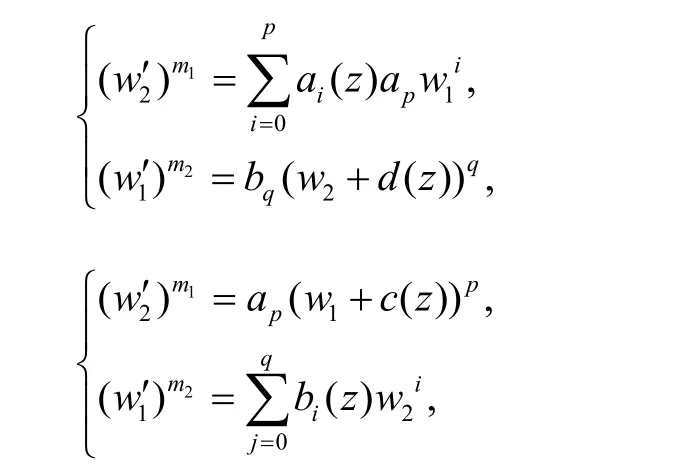
2012年,高凌云还研究了Malmquist型复差分方程组,得到如下结论:
定理E[3]设.如果复差分方程
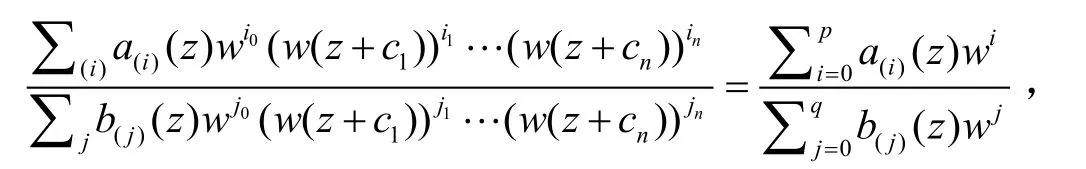
2013年,高凌云再研究了复差分方程
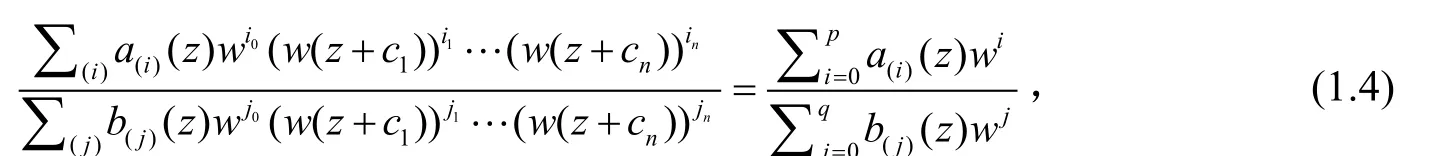
得到下述结果:
定理B[4]设如果复差分方程(4)存在一个有限级的超越亚纯解,则其中
对如下一类高阶非线性代数微分方程:

其中:
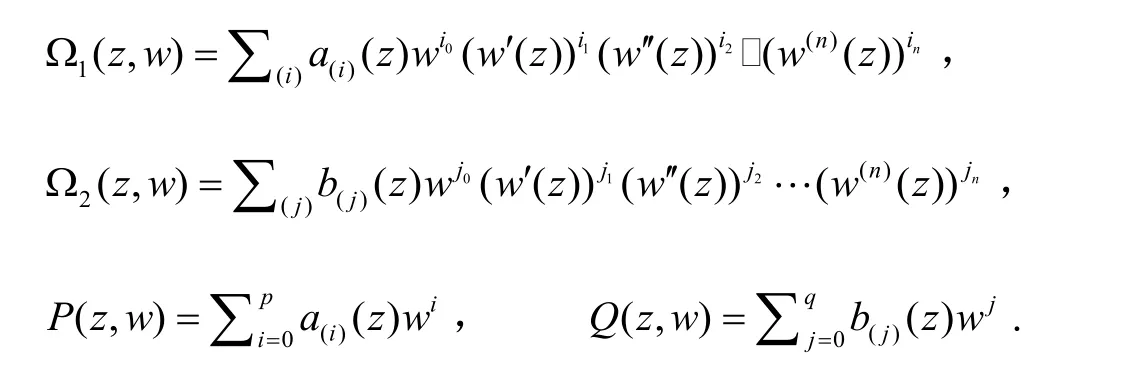
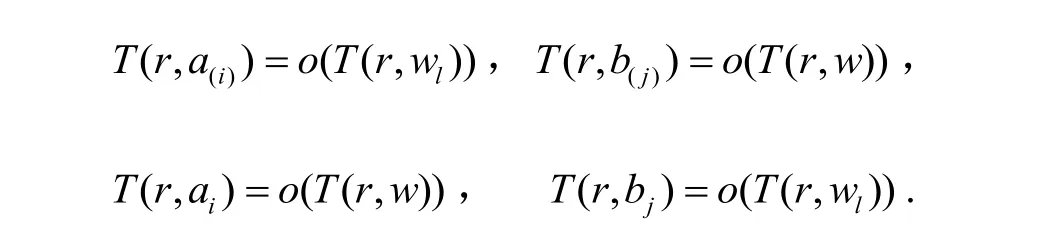
W1(z,w)
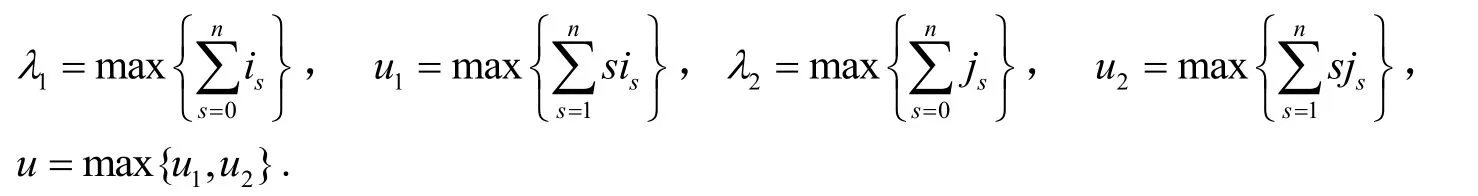
有如下定义:
设u(z)为一v值代数体函数,z0是w(z)的一个极点,则在z0的一个邻域内,我们有w(z)的展开式
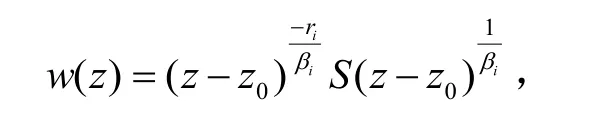
定义[5]设w(z)是v值代数体函数,令:
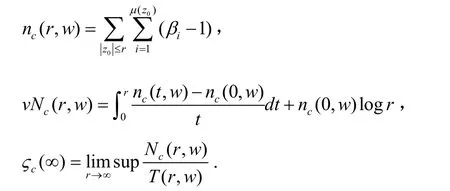
由定义1,我们容易得到:
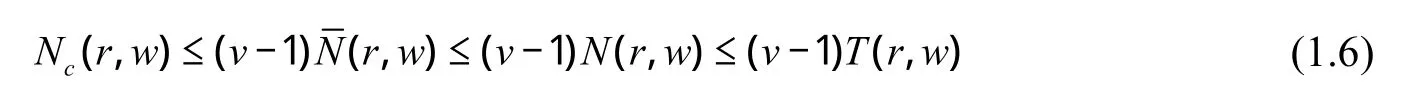
本文利用Nevanl inna值分布理论,在高凌云等人研究的结果的基础上,我们研究了高阶非线性微分方程方程(1.5)的亚纯解的存在问题,得到了高阶非线性代数微分方程(1.5)的超越亚纯解有如下结论:
定理 如果高阶非线性微分方程(1.5)存在一个有限级的代数体函数的超越亚纯解,则:
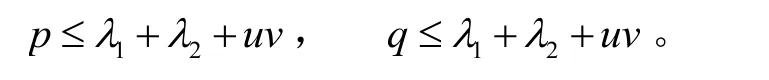
2 主要引理
引理1[6]设是关于w(z)的不可约的有理函数,系数如果w(z)是亚纯函数,则有:是亚纯函数。
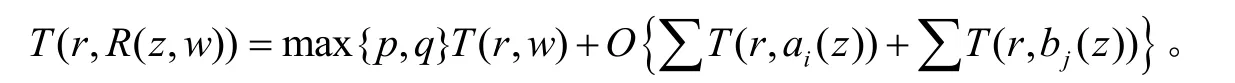
引理2[7]设w(z)是v值代数体函数,和如上所述,则有:
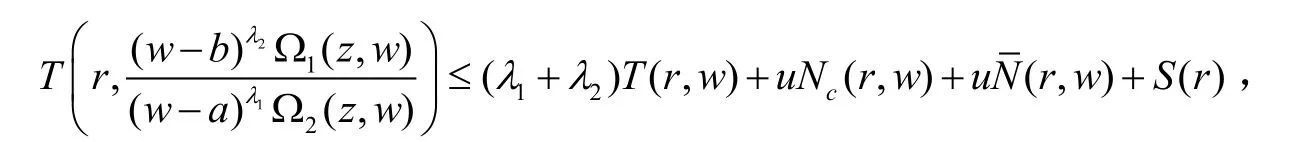
其中
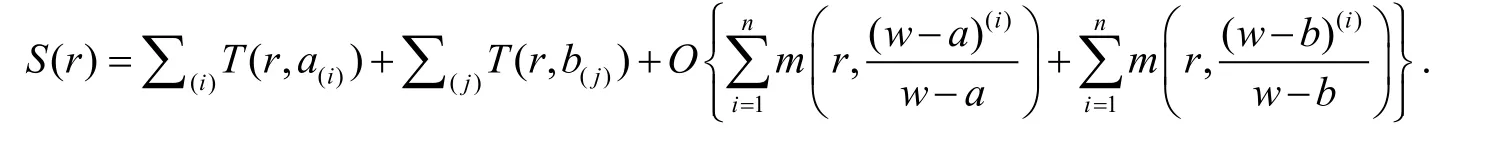
3 定理的证明
证明 (1)微分方程(1.5)可表示为:
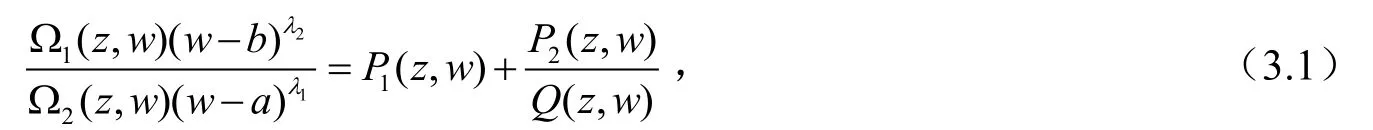
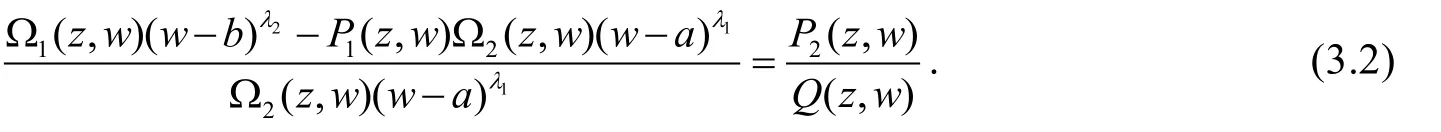
应用引理2于(3.2)式有:
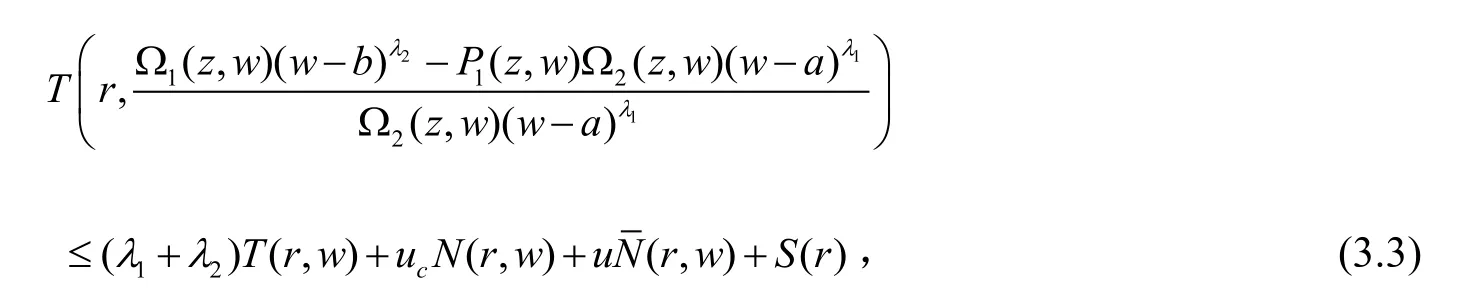
其中:
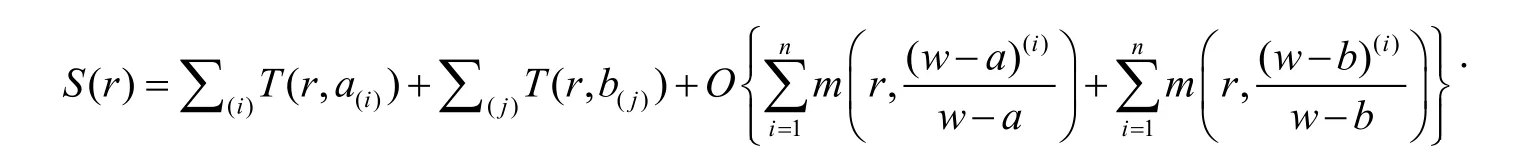
另一方面,由引理1有:
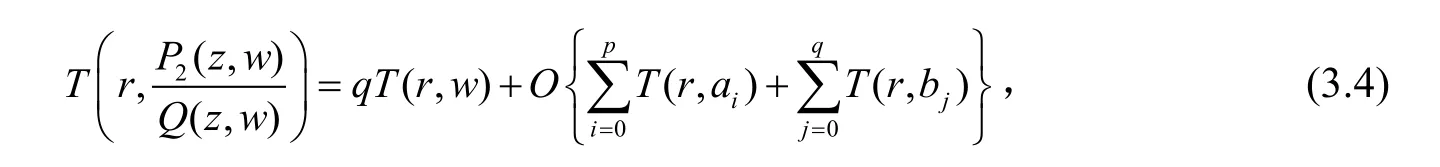
由(3)和(4)以及(6)我们可得:
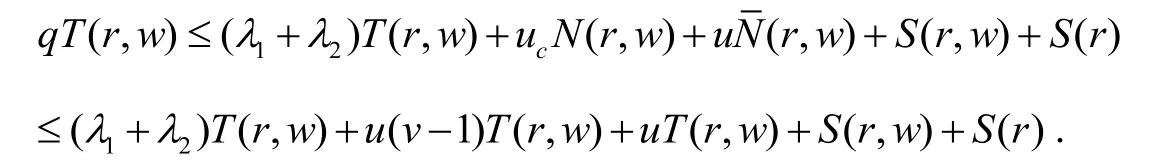
故:
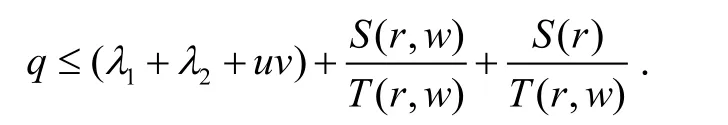
时,可能除去一个对数测度为有限的例外值集I,我们有:
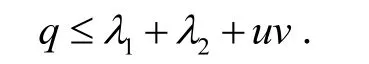
(2) 微分方程(1.6)也可表示为:

由(3.5)式可得:
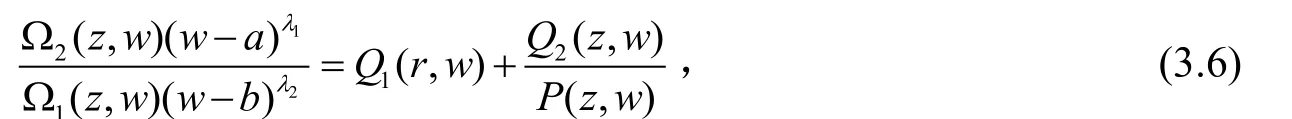
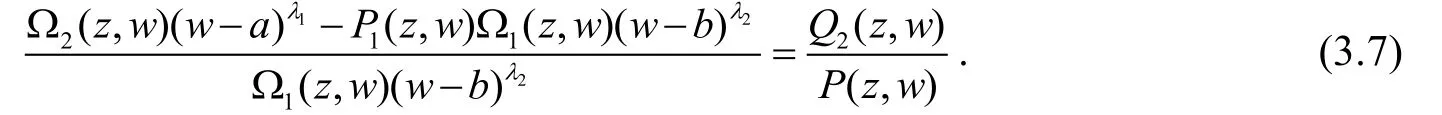
应用引理2于(3.7)式有:
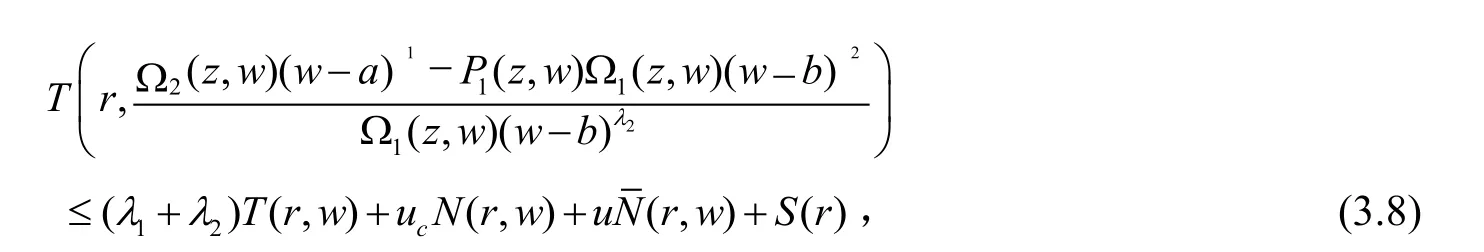
其中
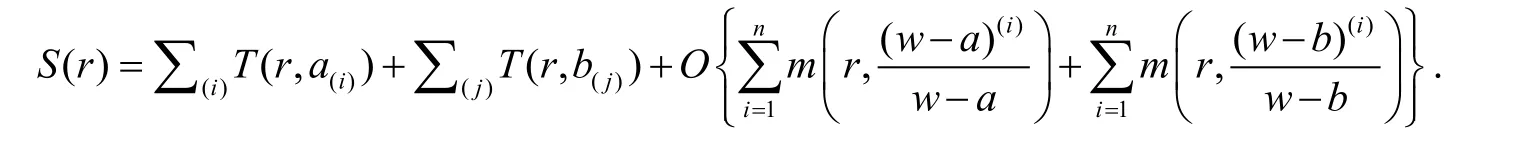
另一方面,由引理1有
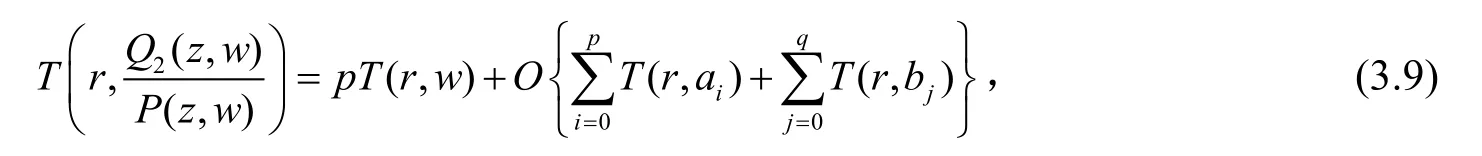
由(3.8)和(3.9)以及(1.7)我们可得

故
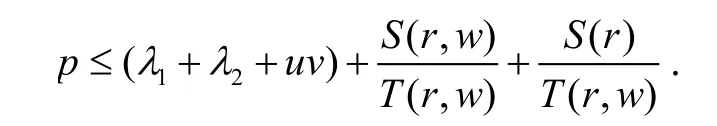
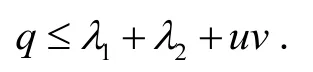
综上(1)和(2)可得,定理成立。
参考文献:
[1]Toda N.On the conjecture of gackstatter and laine concerning the differential equation[J].Kodai Math.J.,1983(6):238-249.
[2]高凌云.具有允许解的代数微分方程组的形式[J].系统科学与数学,2004(1):96-101.
[3]高凌云.M almquist型复差分方程组[J].数学学报,2012(2):293-300.
[4]高凌云.高阶差分方程的解[J].数学学报,2013(4):451-458.
[5]Toda N,Kato M.On some algebraic differential equationsw ith adm issible algebroid solutions[J].Proc.Japan acad.A,1985(61):325-328.
[6]肖修治,何育赞.代数体函数与常微分方程[M].北京:科学出版社,1988.
[7]王钥,高凌云.关于一类高阶非线性代数微分方程解的增长级[J].应用数学学报,2014(1):37.
[8]高凌云.Malmquist型复差分方程组[J].数学学报,2012(2):293-300.
[9]Gackstatter F,Laine I.Zur theorir der gewohnlichen differential chungenim Komplexen[J].Ann Polon Math,1980(38):259-287.
[10]高凌云.高阶微分方程允许解的存在性[J].数学杂志,2003(3):381-384.
[11]肖修治,何育赞.代数微分方程的Malmquist定理[J].科学通报,1982(10):583-586.
[12]金瑾,李泽清.一类高阶非线性微分方程组的亚纯允许解[J].应用数学,2014(2):292-298.
[13]金瑾.高阶微分方程解与其小函数的关系[J].高校应用数学学报,2013(1):43-51.
[14]金瑾.关于一类高阶齐次线性微分方程解的增长性[J].中山大学学报,2013(1):51-55.
[15]金瑾.一类高阶齐次线性微分方程解的增长性[J].华中师范大学学报,2013(1):4-7.
[16]金瑾.单位圆内高阶齐次线性微分方程解与小函数的关系[J].应用数学学报,2014(4):754-764.
[17]金瑾.一类高阶齐次线性微分方程的亚纯解与其小函数的复振荡[J].工程数学学报,2014(3):399-405.
[18]金瑾,樊艺,左建军,武玲玲.一类亚纯系数高阶非齐次线性微分方程解与小函数的增长性[J].上海大学学报,2014(6):726-732.
[19]金瑾.关于高阶线性微分方程解与其小函数的增长性[J].上海交通大学学报,2013(7):1155-1159.
(责编:彭麟淋责校:明茂修)
Research of Solutionsof a Classof Higher-order Nonlinear Algebraic Differential Equations
JIN Jin1,HUANGDiao2
(1.SchoolofScience,Research Institute ofCircular Economy,Guizhou University ofEngineering Science,Bijie,Guizhou 551700,China; 2.Faculty ofScienceofGuizhou NationalitiesUniversity,Guiyang,Guizhou550025,China)
Abstract:Using Nevanlinna theory for value distribution of meromorphic function,we investigate the problem ofmeromorphic solution of a class of higher-order nonlinear algebraic differential equation,and ob⁃tain one resultwhich due toGao Lingyun etc is in proved and generalized.
Keywords:Algebraic Differential Equation;Meromorphic Solution;Algebraic Function;Theory of Value
中图分类号:O1
文献标识码:A
文章编号:2096-0239(2016)01-0126-06 O1
作者简介:金瑾(1962-),男,贵州大方人,贵州工程应用技术学院理学院、循环经济研究院教授,贵州民族大学硕士生导师。研究方向:复分析。
基金项目:贵州省科学技术基金资助项目“复微分方程解的复振荡研究”,项目编号:2010GZ43286;贵州省科学技术基金资助项目“微分方程解的理论及应用研究”,项目编号:2012GZ10526;贵州省毕节地区科研基金资助项目“喀斯特地区石漠化时空格局及其评价体系的模型研究”,项目编号:[2011]02。
收稿日期:2015-10-20

