教学实例的线性代数课程教学方法探讨

童姗姗， 朱玉清， 连冬艳

(南阳理工学院 数学与统计学院，河南 南阳 473004)



教学实例的线性代数课程教学方法探讨

童姗姗， 朱玉清， 连冬艳

(南阳理工学院 数学与统计学院，河南 南阳 473004)

摘要：基于教学实践中的已取得良好成效的教学实例，针对传统线性代数教学过程中的弊端，从3个方面进行教学方法的改革探索：①归类记忆法，包括形式归类、内容归类、方法归类，实现“知其一而知其他”，减轻学生记忆负担；②寓教于乐，观察抽象概念的语言叙述特征和符号表示特征，通过联想、比喻、拟人方法化抽象为形象，挖掘数学内涵美，调动学生学习兴趣；③编辑逻辑主线，把“线”交给学生，使其“顺藤摸瓜”，体验自己挖掘知识的快乐，培养学生的论证能力和推理能力．

关键词：教学实践；线性代数；归类记忆；寓教于乐；逻辑主线

0引言

线性代数作为理工科学生的必修基础课程，其知识结构的严密逻辑性、连贯性、实用性为其他专业课的学习提供了重要的奠基作用，有助于培养学生科学的逻辑思维能力，是一门不可或缺的工具课程．但是由于线性代数课程的抽象性和学时的有限性，传统的教学方法使学生常常苦恼于理不清学习头绪，甚至视线性代数为“枯燥无味”的代名词，导致不够积极主动，没有学习兴趣．因此如何改革本课程的教学方法，充分激发学生的学习兴趣，使学生在线性代数的海洋里轻松畅游，进而提高教学效果，是教学研究中亟待解决的问题．笔者根据课程的结构特征，结合其他先进教学实践，经过长期的认真思考，总结了自己的一些教学方法．

1归类记忆，减轻记忆负担

线性代数课程大多开课于第二学年，正是学生开始专业课的学习时期，学习时间较为紧张，而作为公共基础课程，知识材料的大量积累使学生有不胜负荷的心理，因此怎样使学生利用最短的时间摄取最大量的知识要点，是教学中首要考虑的问题．记忆是学习的重要任务，琐碎、繁多的数学概念、性质、定理、推论、步骤是轻松快速记忆的“天敌”，故应该授予学生有效的记忆方法，缩短学习时间，消除学生对记忆的畏惧心理，从而提高理解力和记忆效率．

归类法是所有记忆方法的基础．学生往往对零散的知识没办法，记住这个，就忘了那个，翻来覆去，在脑海中也没留下什么，即使记住了，保持的时间也很短，到底什么样的知识结构能让学生乐于接受，并且能在其脑海中留下深刻痕迹呢？无疑是具有形态的知识结构，即通过带领学生对琐碎知识进行观察、比较来组织知识模块，从而达到“知其一而知其他”的学习效果．当然，在学习与复习中对不同种类的知识点的记忆要用不同的归类方法．结合案例，下面谈谈如何运用归类法展开线性代数[1]课程的教学实践.

1.1形式归类

形式归类即根据模式直观找到不同概念之间的联系[2]，从而对数学概念知识模块进行归类，这种方法是最为直接有效的． 例如学习完矩阵乘法、转置、方阵的行列式、逆矩阵后，对这些概念的性质进行梳理就可找到它们之间的联系．

1.2内容归类

内容归类是指根据语言符号系统的特点将同一概念所对应的不同问题系统化，排列整齐，方便学生提取．内容归类往往可以用图表等直观的形式表示出来，一目了然，避免了杂乱无章．例如对于求抽象矩阵的特征值与特征向量，设λ是n阶方阵A的特征值，非零向量q是方阵A对应于特征值λ的特征向量，则有

1)kλ是方阵kA的特征值，且q是方阵kA对应于kλ的特征向量；

3)λm是方阵Am的特征值，且q是Am对应于λm的特征向量；

4)φ(λ)=a0+a1λ+…+amλm是矩阵φ(A)=a0E+a1A+…+amAm的特征值，且q是φ(A)对应于φ(λ)的特征向量；

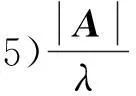
以上内容可归类如表1所示.

表1　抽象矩阵的特征值与特征向量

1.3方法归类

求方阵特征值与特征向量、矩阵的对角化(求可逆矩阵)、实对称矩阵的对角化(求正交矩阵)、正交变换法化二次型为标准型的计算步骤[3]联系紧密，极易混淆．方阵特征值与特征向量的计算是矩阵对角化、实对称矩阵对角化、正交变换法化二次型为标准型的基础，但是后三者不需要全部的特征向量；矩阵对角化过程需要先判断是否可对角化，若可对角化，才可以构造出可逆矩阵；实对称矩阵一定可以对角化，所以无需判断，但是需要将特征向量进行正交规范化；正交变换法化二次型为标准型与实对称矩阵对角化(求正交矩阵)是同一问题的两种不同提法，解法基本相同，只是前者计算过程的最后需写出标准型，如果不将这4个问题的计算步骤之间的联系区分清楚，学生会经常犯以下错误：

1)求方阵特征值与特征向量过程中，没有写出基础向量的线性组合形式，即没有给出各个特征值的全部特征向量；

2)实对称矩阵对角化过程中，没有对特征向量进行正交规范化就构造矩阵；

3)视矩阵对角化(求可逆矩阵)与正交变换法化二次型为标准型为同一问题的两种不同提法；

4)正交变换法化二次型为标准型过程中，最后没有给出二次型的标准型．

为了避免上述错误，考虑制作一个关于这4个问题的计算方法流程图，让学生体会这4种计算的联系和区别，同时也培养了学生比较、分类、归纳的学习能力．归类要注意完整性和标准多样性，要明确归类的目的和方向，避免不同类知识材料相互干扰，保证学生体会到化繁为简的思想，这就要求教师查阅丰富的相关资料，仔细整合，再确定具体归类的模块．再者，归类要结合各个班级学生的水平，需要根据学生的实际学习情况来确定，不同的学习程度要制订不同的归类方案．最后，授人以鱼不如授人以渔，教师要把好本领传授给学生，培养学生归纳知识的能力，从而实现教学相长，提高自己的教学水平和学生的学习效率(图1)．

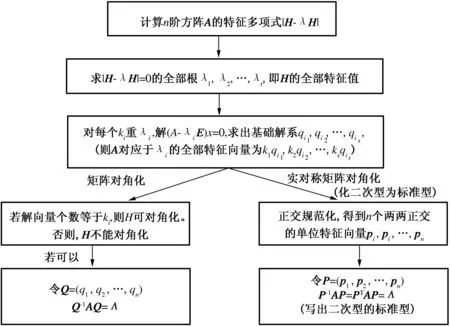
图1　计算方法流程图Fig.1　Flow chart of calculation method

归类法可以使学生理清思路，抓住重点，从繁杂的记忆信息库搜索中赢得时间，故成为大多数学生喜欢的一种记忆方法，笔者在归类教学实践中也获得了较好的教学效果．

2寓教于乐，体现数学的内涵美

教学中为避免枯燥、繁琐等数学印象对学生的影响，可以尝试采用与生活常识紧密相关的教学方法来表达抽象的数学概念．观察教材中的概念特征(包括符号特征、语言叙述特征)，通过联想、比喻、拟人手法使数学中干巴巴的公式和枯燥的语言叙述生动起来，挖掘数学的内涵美，寓教于乐，令学生感受到数学与生活在理念上的联系，从而调动学生的学习兴趣，使学生快速、牢固地理解和掌握相关抽象概念．在高等数学中就有一个很生动的例子，例如无穷小量乘以无穷小量、有界量结果是无穷小量；无穷小量乘以无穷大量的结果可能是无穷小量、无穷大量或有界量.对此可以形象寓意为：很少或有限的努力(无穷小量乘以无穷小量、有界量)是不会达到成功的(结果是无穷小量)，想要成功(得到无穷大量)必须付出足够大的努力(无穷小量乘以无穷大量)，但也要有承担失败的勇气(结果可能为无穷大量，也可能为无穷小量、有界量).如此对抽象结论赋予了通俗的生活哲理，一方面使数学概念形象起来，学生就乐于去对知识进行再认识，提高记忆品质；另一方面，让学生体会到了数学的内涵美，教育学生要发奋努力，对任何事情要有持之以恒的态度．以下还有几个生动的例子：

例1对矩阵乘法Cm×n=Am×sBs×n的乘法规则讨论．

1)可乘性：左矩阵的列数等于右矩阵的行数，联想到赵迎歌曲“手牵手，一起走”．

2)乘积矩阵形状：行数等于左矩阵的行数，列数等于右矩阵的列数，联想到广告词“伸出你我的手，共筑美好未来”．

3)乘积矩阵元素：第i行第j列元素cij等于左矩阵第i行元素与右矩阵的第j列对应元素乘积之和．这个过程就可比喻为：一个人在人生的每一个阶段(A的每一行)都要完成所有必要完成的事情(B的所有列)，才能铸就最完整的人生(乘积矩阵C)．

例2区分余子式(代数余子式)、r阶子式、顺序主子式．

余子式(代数余子式)、r阶子式、顺序主子式[4]这3个概念的定义非常相似，都是对矩阵进行行、列及元素取舍后得到的行列式，取舍的部位不同，得到的结果就不同．学生在用到这3个概念时，经常分不清，这里，可以把矩阵看作一块豆腐，教会大家“切豆腐”的方法：

1)切两刀，取豆腐，舍刀痕，得到的就是余子式(代数余子式)；

2)切r刀，取刀痕，舍豆腐，得到的就是r阶子式；

3)切两刀，只取左上角的那块方形豆腐，得到的就是顺序主子式．

例3行列式按行(列)展开的这节中有两个重要结论，一是定理(行列式按行(列)展开法则)：n阶行列式D=det(aij)等于它的任一行(列)的各元素与其对应的代数余子式乘积之和；二是推论：行列式的某一行(列)的元素与另一行(列)对应元素的代数余子式乘积之和等于0．即

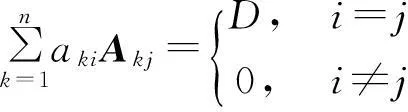
由于两个结论的语言叙述和符号表示形式很相似，导致有许多同学把这两个结论记反，即n阶行列式D=det(aij)等于它的任一行(列)的各元素与另一行(列) 对应元素的代数余子式乘积之和；行列式的某一行(列)的元素与其对应元素的代数余子式乘积之和等于0．为了避免这种错误，观察、揣摩其中的语言叙述和符号表示的特点，可以分别赋予这两个结论这样的寓意：定理说明一个人只有专注努力自己的目标(任一行(列)的各元素与其对应的代数余子式相乘)，才能获得最圆满的结果(乘积之和等于行列式的值)；推论说明一个人如果只想窥探他人的所得(某一行(列)的元素与另一行(列)对应元素的代数余子式相乘)，最终只会落得两手空空(乘积之和等于0)．

这种教学方法可以化抽象为形象，创造和谐轻松的学习氛围，使抽象的线性代数课程充满趣味，调动学生的学习热情和兴趣，提高记忆的持久性．将教学美育的思想渗透到教学中，对学生学习抽象的数学提供了辅助作用，可在一定程度上推进教学改革，但是要避免过于感性，导致错误．

3编织逻辑主线，顺藤摸瓜

线性代数的概念之间联系紧密，环环相扣，因此在教学过程中，摸清知识的“脉搏”就很重要，即把已学过与即将学到的单元知识有机组合起来，编织逻辑主线，构建知识脉络，方便学生快速有效地了解各个章节之间的联系，然后顺藤摸瓜，在严谨的逻辑思维藤上摘下一堆堆知识的果实．

例5矩阵的运算规律相对于数的运算规律，最大的不同点在于矩阵的乘法运算不满足交换律和消去律，即AB=BA不一定成立；AB=AC且A≠O不能推出B=C；AB=O不能推出A=O或B=O．通过举例说明，可以充分证实这些结论，接下来留给学生问题：在什么条件下，这些不成立的就能变成成立的呢？

引入逆矩阵后，若矩阵A可逆，则存在逆矩阵A-1，满足“AA-1=A-1A=E”，即一个可逆矩阵与其逆矩阵是满足乘法交换律的，且对于“AB=AC”和AB=O”，在其左右两边同时左乘A-1，就可以分别实现“B=C”和“A=O或B=O”，因此得出新的结论，即AB=AC且A可逆⟹B=C；AB=O且A可逆⟹A=O或B=O．接下来再考虑：如果矩阵不是方阵，需要满足什么条件时可实现“B=C”和“A=O或B=O”呢？

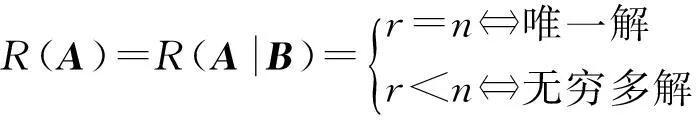
这个教学过程不仅是编织逻辑主线的过程，也是一个逻辑论证的过程，使学生体验到自己挖掘到知识的快乐，在很大程度上培养了学生的论证能力和推理能力．

4结束语

总之，线性代数教学中，应该细心观察，挖掘合适教学素材进行归类记忆教学、美育教学，编辑逻辑主线以提高教学效率[6]，多角度培养学生的创造能力，实现减轻记忆负担、寓教于乐、顺藤摸瓜的教学效果．

参考文献

[1]朱玉清.线性代数[M].北京：科学出版社,2012:22-45.

[2]张广祥,张奠宙.代数教学中的模式直观[J].数学教育学报,2006,15(1):1-4.

[3]同济大学数学系.工程数学：线性代数[M].北京：高等教育出版社,2007:63-77.

[4]董晓波.线性代数[M].南京：南京大学出版社,2007:78-86.

[5]张启明,唐先华.类比法在线性代数教学中的运用[J].当代教育理论与实践,2011,03(10):76-78.

[6]李曦.工科院校线性代数教学改革的探索与实践[J].中国校外教育,2011 (8):133.

Exploration on Teaching Method of Linear Algebra Based on Teaching Practice

TONG Shanshan， ZHU Yuqing， LIAN Dongyan

(SchoolofMathematicsandStatistics，NanyangInstituteofTechnology，Nanyang473004，China)

Abstract:Based on the teaching instance that has made good effectiveness of teaching instance, aiming at the disadvantages of traditional teaching process, the reform of teaching methods is explored in three aspects. The first is classification memory method, including form classification, content classification and method classification, whose aim is to achieve “know one of and known other” and to reduce the students’ burden of memory; the second is entertainment: observing the abstract concept of language features and symbolic representation characteristic, transforming the abstract concept into image description by association, metaphor, personification method to mine the mathematical beauty of connotation and arouse the students’ interest in learning; the third is editing the logic thread: putting the “line” to students for tracking by clues and experiencing the happiness of getting knowledge personally to cultivate students’ argumentation and reasoning ability.

Key words:teaching practice; linear algebra; classified memory; edutainment; logic thread

中图分类号：G642.4

文献标志码：A

文章编号：1007-0834(2016)01-0065-05

doi：10.3969/j.issn.1007-0834.2016.01.015

作者简介：童姗姗(1986—)，女，河南南阳人，南阳理工学院数学与统计学院教师．

基金项目：河南省科技攻关计划项目(122102210060)；南阳理工学院教学改革专项研究项目(NIT2013BK-09)；南阳市科技计划项目(RKX06)

收稿日期：2015-09-26