道路载荷谱采集可靠度评判方法的研究与应用

曾发林，阮 洋，李建康

(1.江苏大学汽车工程研究院, 镇江 212013; 2.江苏大学汽车与交通工程学院, 镇江 212013)

2016015

道路载荷谱采集可靠度评判方法的研究与应用

曾发林1，阮 洋2，李建康1

(1.江苏大学汽车工程研究院, 镇江 212013; 2.江苏大学汽车与交通工程学院, 镇江 212013)

本文中对道路载荷谱采集可靠度的评判方法进行了研究。首先探讨时域标准差参数与基于雨流计数法计算疲劳累积伪损伤值之间的关系,得出伪损伤值与标准差正相关的结论。然后基于以上结论,提出一种同车轴载荷谱归一化标准差评判方法,并成功应用于载荷谱采集监测过程。最后通过载荷谱的雨流参数拟合,表明标准差也影响雨流变程和均值的分布性状。本研究的结果表明:该方法理论意义清晰,具有提高载荷谱采集可靠性、节约试验时间的工程应用价值,为后续室内道路模拟试验奠定基础。

道路载荷谱;归一化标准差;雨流计数法;室内道路模拟试验

前言

汽车耐久性工程中的关键是获得可靠的载荷数据，而这些载荷数据必须能够准确代表用户实际使用过程中汽车零部件的累积损伤[1]。用于室内道路模拟试验的目标道路载荷谱(下文简称载荷谱)的采集属于随机过程，其每个样本中各对应元素时间历程具有一定的离散性[2]。在汽车试验场采集数据时，由于受到实际行驶车速的非平稳性、驾驶员的驾驶习惯、测量仪器的非线性失真和行驶环境中存在风阻、坡阻和惯性等因素影响[3]，使载荷谱信号具有非线性非平稳特征，严重情况下会导致在台架试验迭代环节出现结果发散、得不到合适驱动谱的问题。倘若后期才发现载荷谱存在瑕疵，补救方法有限，重新采集则严重浪费人力与物力。因此，实时监测载荷谱采集过程的可靠度和有效性显得非常重要。

本文中通过仿真数据与工程实际载荷谱的计算分析，探究了样本标准差S和基于雨流计数法算出的疲劳累积伪损伤值D(下文简称损伤D)之间的关联性，首次提出同车轴载荷谱归一化标准差评判法，并初步研究了针对载荷谱雨流参数分布模型的拟合问题。实际工程应用表明，本文中所述方法能够提高数据采集的可靠度，具有较高的工程应用价值与指导意义。

1 参数计算介绍

1.1 雨流计数法简介

雨流计数法属于典型的双参数法，双参数分别为动强度(雨流域变程Range，相邻峰谷值之差，两倍于循环振幅)和静强度(雨流域均值Mean，相邻峰谷值的平均值)。最终计数所得的雨流矩阵记录了三维数据——变程Range、均值Mean及相应频次Cycle。文献[4]～文献[6]中对雨流计数法有详细介绍，可概括为3步：

(1)将载荷谱的幅值范围等级划分后进行迟滞滤波，删除不能构成损伤的小量变程循环；

(2)提取具有损伤性的子循环，统计Range、Mean和Cycle，形成雨流矩阵；

(3)根据预先设定的疲劳-寿命曲线和Miner线性疲劳累积损伤理论[7]来估算损伤值。

雨流计数法的统计结果能够比较全面地反映载荷的真实特征，且主要应用于以下方面：

(1)删除微小损伤循环，压缩时域载荷谱以达到加速疲劳试验的目的；

(2)通过雨流矩阵运算，外推出时程更长的载荷谱信号，克服某些强化路面距离短的不足；

(3)估算疲劳寿命和编制疲劳试验载荷谱[8]；

(4)基于损伤等效原理，得到各强化道路路段的组合系数。

1.2 标准差计算

在实际处理中，一般平稳物理现象的随机数据都可以认为是各态历经的，所以能够用单个样本(时间历程记录)来测定其特征。道路载荷谱属于随机响应信号，具备不规则、不能重复等特征，须要使用统计分析方法对其进行描述与分析。因此，采用样本标准差S作为总体标准差σ的估计值，计算公式[9]为

(1)

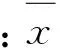
2 评判法提出的工程背景

载荷谱的采集过程中，一般只能进行短时间(距离)的采集。本文中主要研究两组实测载荷谱，其中某型三轴重型运输车的载荷谱采集于安徽定远汽车试验场(其典型轴头加速度计安装位置见图1(a))，包括比利时路、搓板路等典型强化路面。行驶车速按照试车场的试验标准进行，采样频率为400Hz，称为1#道路载荷谱。另外，某型双轴SUV车的道路载荷谱采集于湖北襄樊汽车试验场(其典型轴头加速度计安装位置见图1(b))，包括搓板路、长波路等强化路面，采样频率为200Hz，称为2#道路载荷谱。

图1 不同测试车型的典型位置加速度计安装

1#道路载荷谱在后期的室内道路模拟试验的迭代环节中，前轴左轴头与后轴右轴头在卵石路和扭曲路工况下的迭代结果无法收敛，延误正常的台架试验进度。通过观察扭曲路下的PSD(图2)发现，前轴左轴头和后轴右轴头在3.0Hz以下低频范围内的能量比其他4个轴头大得多，而其余各轴的主要能量集中在3.5和11.0Hz左右，进而断定该两轴头传感器在采集过程中受到干扰。若作3Hz低频范围的滤波处理，则违背了载荷谱编辑前后PSD需一致的原则[10]，并且无法全面地考察扭曲路况下的损伤效果。若在前期采集过程中及时发现问题，则可排除故障，避免物力的浪费。因此，运用一种简捷有效的监测评判法显得很有必要，基于时域参数计算方便的优点，着重考察时域均值μ、标准差S与损伤D的关系。

图2 扭曲路工况下的载荷谱PSD计算结果

3 数值仿真

通过构造多组幅值服从正态分布的仿真随机加速度信号，更改均值μ和标准差S两个统计参数与损伤D之间的相关性。设所有仿真信号的采样频率为500Hz，总采样时间为4s。

3.1 时域均值与损伤的关系

第一组仿真加速度信号的均值μ变化范围为0～200m/s2，增幅为10m/s2，标准差S统一为1m/s2。为方便统计，将损伤D与μ进行归一化(图3)，发现μ与损伤的关联性不是很有规律，非线性特征很强，意味着μ对最终损伤计算的影响不大。每组仿真信号的疲劳循环统计总数基本上在650次左右。

图3 时域均值μ与损伤D的关系曲线

同时，观察雨流矩阵的形状图(图4)可发现，Mean具有以μ为对称轴进行分布的特征。在编制特定疲劳载荷谱时(如随机非各态历经过程载荷谱)，须要考虑Mean的影响。

图4 典型仿真信号雨流矩阵

3.2 标准差与损伤的关系

第二组仿真数据的标准差S取值范围为0～200m/s2，增幅为10m/s2，时域均值μ统一为0。仿真结果表明：幅值服从正态分布的随机信号，其疲劳循环数基本保持不变，并且S和D在双对数坐标下呈现线性关系(线性坐标下为幂函数形式)，设定拟合公式为

D=ea·Sb或lnD=a+blnS

(2)

式中:a和b为待定参数，拟合结果见图5。文献[11]中指出，描述材料疲劳-寿命曲线的最常用形式就是幂函数形式，则待定参数a和b应与材料性质、应力比、加载方式等因素有关。

通过相关系数r[11]可判断变量x与y之间的线性相关程度，r由偏差乘积和Lxx，Lyy，Lxy定义，即

(3)

r的绝对值越接近1，表明两参数的线性相关程度越强。经计算，在双对数坐标下的D-S线性相关系数达到0.999 9，线性相关程度很高，说明拟合公式正确合理。

图5 时域标准差S与损伤D关系曲线

4 评判法的具体内容

4.1 初步假设

先作假设：

(1)不同路况采集所得的载荷谱可以看作是各态历经的稳态随机过程；

(2)车辆可以理想为对称结构，且左、右车辙的路面不平度系数相等[12]，同轴的左右两个轴头结构、配重和力学性能参数相似。

基于以上两点假设，同轴轴头载荷谱除存在相位差的可能性之外(如扭曲路)，两者的标准差S与损伤值D应该处于同一量级水平。因此，可将二者载荷谱的S与D同时作归一化处理。譬如，若前轴的左轴头载荷谱标准差大于右轴头，则将左轴头载荷谱标准差归一化为100%。同一强化路面下时间序列样本的选取、比较、分析，应遵循具有相等时间长度的原则。

将1#道路载荷谱在各路况下作归一化S和D计算，见图6(限于篇幅，不通过列表形式给出详细计算结果)。结果表明，在各强化路面下，D与S存在正相关关系，意味着如果某轴头载荷谱的S值大于另一轴头，那么其D值必定相对较大。同时，图6存在两个归一化比列不协调的异常现象：

(1)在卵石路工况下，前轴右轴头载荷谱归一化S值为71.08%(后轴左轴头归一化S值为66.00%)，而其归一化D值为32.45%(后轴左轴头归一化D值为23.82%)；

(2)在扭曲路工况下，前轴右轴头载荷谱归一化S值为28.04%(后轴左轴头载荷谱归一化S值25.02%)，归一化D值为1.42%(后轴左轴头归一化D值为0.52%)。

图6 某运输车载荷谱归一化S和D计算结果

通过图6可以初步判断在这两种路况下，前轴和后轴必定存在某个轴头的载荷谱采集存在问题(由第2节已知前轴左轴头和后轴右轴头信号采集有误)。

4.2 标准差同雨流计数法的联系

从3.2节和4.1节的内容，总结出一个普遍规律：伪损伤D正相关于时域标准差S，即D∝S。从概率意义理解，S值越大，即载荷谱的幅值越离散，则经雨流计数得到大变程循环的可能性就越大，从而得到更高的伪损伤值。S计算过程比D计算过程更为简捷，且易于编程，省去雨流计数再计算损伤的繁琐过程。

名义上各试验路段每一循环的载荷是一样的，实际上不可能完全一致，因此在理论上为了精确地获得载荷谱的平均值，须要进行无限次测量，但明显不现实。如何在有限的采集循环里，提高采集可靠度很有工程意义。基于以上分析，提出“同车轴载荷谱归一化标准差评判法”，根据S值的大小来判断各类型载荷谱损伤，尝试用于实时监测道路载荷谱的现场采集过程中，进而判断信号采集的正常与否。当某同车轴的两轴头所测载荷谱的归一化S值小于某一阈值时，则说明在该强化路况下的采集存在问题，有必要重新采集，避免整个采集循环失效。因为受到测量车辆、路面参数等众多因素的影响，该阈值的设定具有不确定性，建议取值不可低于75%，具体取值需要更多的工程经验加以确定。

4.3 评判法的应用工程实例

应用本文中“同车轴载荷谱归一化标准差评判法”，实时监测2#道路载荷谱的采集试验。通过实时计算归一化标准差值，并规定阈值为78%，监测各强化道路载荷谱的采集情况。最终所测载荷谱正常，某一采集循环的计算结果见图7(后期增补归一化D值)，并且在后期的台架试验迭代环节中未出现任何问题，表明本文中的方法取得良好效果。表1为某SUV道路载荷谱时域统计参数和雨流域损伤计算结果。它验证了在任何强化道路上，损伤D与标准差S正相关的结论。

图7 某SUV载荷谱归一化S和D计算结果

5 雨流参数拟合

在同一道路载荷谱时间序列当中，假设信号为稳态随机信号，即时域均值μ和标准差S不随时间变化，那么通过雨流计算之后的伪损伤值只与S存在正相关的关系。应用雨流计数法完成对载荷谱的频次统计，对得到的特征参数样本——雨流Range和Mean进行概率分布拟合，找出描述参数分布特征的最佳模型。在无先验经验的情况下，通常选取6种常用分布模型——指数分布、正态分布、对数正态分布、Gamma分布、两(三)参数Weibull对样本进行拟合[13]。根据工程经验，载荷谱的雨流域幅值一般服从正态分布或Weibull分布，雨流域均值服从正态分布。本文中，时域信号的差别通过S识别，雨流域Range和Mean的差别尝试通过多级正态分布函数拟合识别。

表1 某SUV道路载荷谱时域统计 参数、雨流域损伤计算结果

以某运输车在扭曲路工况下的前轴载荷谱分析为例，左轴头和右轴头载荷谱的S值分别是12.671 4和3.552 6m/s2，时域均值μ分别是-0.344 9和0.000 8m/s2，Range和Mean的拟合结果见图8。应用95%置信区间概率图法进行假设检验，发现数据与多级正态分布组合的最佳拟合线最为接近，拟合误差之和接近于零。对比图8(a)和图8(c)可知，左轴头载荷谱的雨流变程范围明显大于右轴头，且前者频次分布主要集中在0～20m/s2，而后者集中于0～10ms2。同时，右轴头雨流均值分布形状(图8(d))的对称性要优于左轴头(图8(b))。表明标准差S的差异，折合到雨流域，则会影响参数Range和Mean的分布形状。

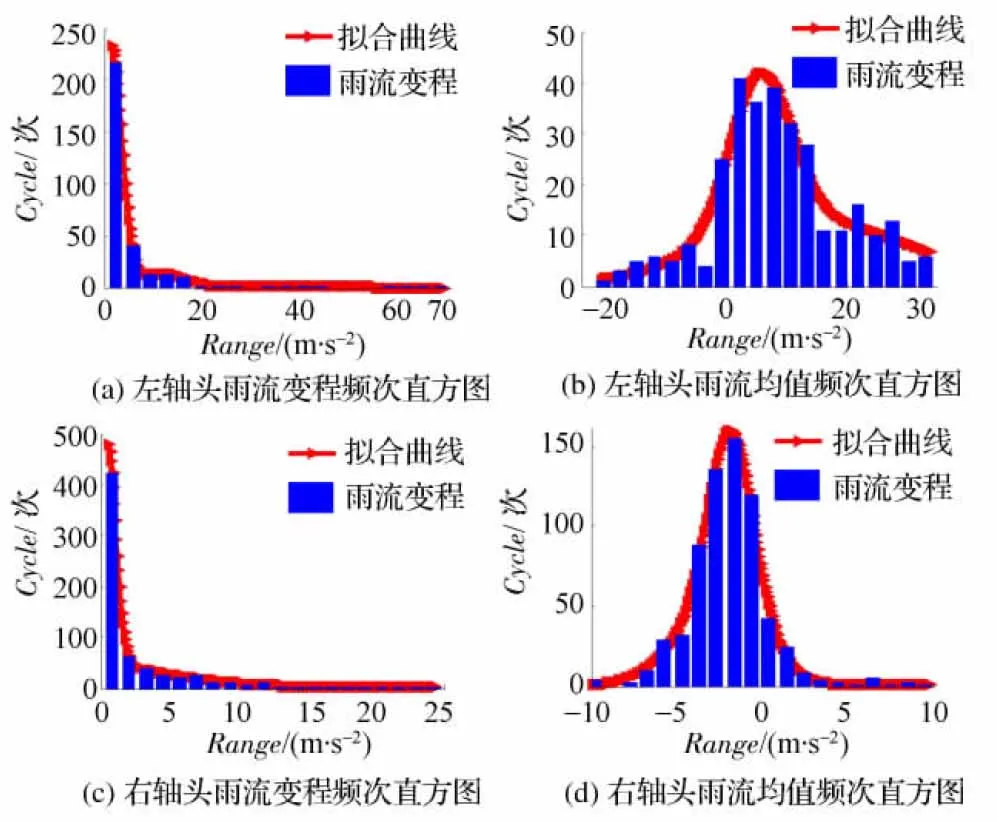
图8 扭曲路工况下前轴载荷谱雨流统计直方图

针对SUV车，以分析搓板路工况下的前轴左轴头载荷谱为例，其功率谱密度函数(图9(a))存在38.8和78.1Hz两个峰值，具有双峰谱特征。文献[14]中假设双峰谱密度的雨流幅值(变程)分布可由两个Weibull分布组合，而本文中通过实际检验，双峰谱雨流变程可分为两个正态分布的组合(图9(b))，且雨流均值需要多个正态分布组合(图9(c))。因为实测载荷谱具有非线性非平稳特征，所有的分布函数拟合只存在理论上的近似，可以肯定的一点是，雨流参数的分布形状与标准差有关联。针对不同路况下载荷谱雨流域Range和Mean的拟合研究，可以指导疲劳载荷谱的编制，限于篇幅原因本文中不作深入探究。

图9 搓板路工况下载荷谱各参数计算结果

6 结论与展望

本文中采用同车轴载荷谱归一化标准差评判法，实时监测道路载荷谱采集，可以提高采集的可靠度，避免人力物力的浪费，为后期台架试验的顺利完成奠定基础。该方法简单高效，实际应用表明其含义直观，使用方便。

(1)正态随机仿真信号的分析结果表明，其标准差与疲劳累积伪损伤值呈对数线性关系；结合实测载荷谱信号的分析结果，得到更为一般的结论，即载荷谱的损伤值与标准差正相关。

(2)通过将不同强化路况下的载荷谱标准差作归一化处理，设定归一化阈值，当同轴载荷谱出现小于阈值时，基本可断定该路况下的采集存在问题，须重新采集。

(3)载荷谱雨流域变程和均值的频次分布特征受标准差的影响，且可由多级正态分布函数进行拟合。

关于归一化S阈值的具体设定等问题，有待更多的道路载荷谱采集试验来验证，且时域标准差与雨流域双参数之间的理论关系，需要大量的工程试验数据进行更为深入的探究。最终，通过理论体系的完善来推广该方法的应用。

[1] 康强,左曙光,周炜.汽车用户道路行驶载荷谱测量及推断方法研究[J].汽车技术,2009(10):55-58.

[2] 张觉慧,金锋,余卓平.道路模拟试验用载荷谱样本选择方法[J].汽车工程, 2004, 26(2): 220-223.

[3] 宋勤,姜丁,赵晓鹏,等.道路模拟试验载荷谱的采集、处理与应用[J].仪表技术与传感器,2011(3):104-106.

[4] 高镇同,熊峻江.疲劳可靠性[M].北京:北京航空航天大学出版社,2000.

[5] CARMEN C, ENRIQUE C, CANTELI, et al. Rainflow Analysis in Coastal Engineering Using Switching Second Order Markov Models[J]. Applied Mathematical Modelling,2012,36(9):4286-4303.

[7] WANG Y S, MA Q H, ZhU Q, et al. An Intelligent Approach for Engine Fault Diagnosis Based on Hilbert-Huang Transform and Support Vector Machine[J]. Applied Acoustics,2014,75(1):1-9.

[8] 唐浩,屈梁生.基于支持向量机的发动机故障诊断[J].西安交通大学学报,2007,41(9):1124-1126.

[9] MANIKANDAN J, VENKATARAMANI B, AMUDHA V. A Noval Technique for Support Vector Machine Based Multi-class Classifier[C]. TENCON 2008. Hyderabad India:TENCON 2008 IEEE Region 10 Conference Publication,2008:1-6.

[10] 连可,黄建国,王厚军,等.一种基于遗传算法的SVM决策树多分类策略研究[J].电子学报,2008,36(8):1502-1507.

[11] 王一,杨俊安,刘辉.一种基于遗传算法的SVM决策树多分类方法[J].信号处理,2010,26(10):1495-1499.

[12] 张庆,刘丙杰.基于PSO和分组训练的SVM参数快速优化方法[J].科学技术与工程,2008,8(16):4613-4616.

[13] 金晶,王行愚,罗先国,等.PSO-ε-SVM的回归算法[J].华东理工大学学报(自然科学版),2006,32(7):872-875.

Study and Application of the Reliability Evaluation Method for Road Load Spectra Acquisition

Zeng Falin1, Ruan Yang2& Li Jiankang1

1.AutomotiveEngineeringResearchInstitute,JiangsuUniversity,Zhenjiang212013;2.SchoolofAutomotiveandTrafficEngineering,JiangsuUniversity,Zhenjiang212013

The reliability evaluation method of road load spectra acquisition is studied in this paper. Firstly, the relationship between the standard deviation (SD) parameters in time domain and the cumulative fatigue pseudo damage calculated by rainflow counting algorithm is investigated with a conclusion that there is a positive correlation between pseudo damage and SD. Then based on the conclusion, an evaluation method of normalized SD of coaxle load spectra is proposed and successfully applied to the monitoring process of load spectra acquisition. Finally the rainflow parameter fitting of load spectra show that the SD also affect the distribution pattern of rainflow range and mean. The results of the study indicate that the method proposed is clear in theoretical sense and has the engineering application value in enhancing the reliability of load spectra acquisition and saving test time, laying the fundamentals for the follow-up indoor road-simulation tests.

road load spectra; normalized standard deviation; rainflow counting; indoor road simulation test

原稿收到日期为2014年4月2日，修改稿收到日期为2014年9月12日。