路面随机激励下轻型货车驱动桥壳疲劳可靠性分析*

卢剑伟,王馨梓,吴唯唯

(合肥工业大学机械与汽车工程学院，合肥 230009)

2016020

路面随机激励下轻型货车驱动桥壳疲劳可靠性分析*

卢剑伟,王馨梓,吴唯唯

(合肥工业大学机械与汽车工程学院，合肥 230009)

本文中对路面随机激励下驱动桥壳的疲劳可靠性进行了分析和优化。首先在ANSYS中建立了某轻型货车驱动桥壳参数化有限元模型，分析了变速工况下随机路面对桥壳的载荷谱，得到了路面随机激励下的桥壳动态响应。在此基础上，根据Miner累计损伤准则，对桥壳在循环工况下的疲劳累计损伤进行了计算，并对其疲劳可靠性进行了评估。最后以桥壳在一定行驶里程内的疲劳可靠性为约束条件，对桥壳进行优化。优化结果改善了桥壳的疲劳可靠性,满足设计要求。

桥壳;随机路面;循环工况;疲劳;优化

前言

桥壳是车辆重要的结构件，用于保护主减速器、差速器和半轴等，使左、右驱动轮的轴向相对位置固定，并支承车架及其上各总成的质量[1]。车辆行驶过程中桥壳受到来自路面的复杂载荷作用，由此导致的疲劳破坏是桥壳的主要失效形式之一[2]。为了提升整车的动力性、燃油经济性、操纵稳定性、平顺性和节约材料成本，如何在保证桥壳疲劳可靠性的基础上对其结构进行优化，是车桥总成设计中面临的一个关键问题。

目前桥壳疲劳可靠性的分析大多是基于静态载荷工况并计入适当的动载系数后进行分析评价[3-4]，经常导致分析结果与工程实践出现矛盾，其主要原因是基于静态工况分析的桥壳可靠性评价方法无法对其疲劳可靠性进行分析评估，相关分析结论可能与实际路面随机激励作用下桥壳的疲劳可靠性有较大偏差。为克服这一问题，本文中以某轻型货车驱动桥壳为例，考察了随机路面输入下桥壳的动态响应，对循环行驶工况下桥壳的疲劳可靠性进行了分析评价，最后根据相关分析结果对其进行结构优化，以提升其疲劳可靠性，相关分析方法和结论可为桥壳的可靠性设计提供有益的借鉴。

1 桥壳的疲劳可靠性分析

1.1 桥壳有限元建模

车辆在行驶的过程中，桥壳主要承受来自路面和钢板弹簧的随机载荷。结合桥壳的结构特征，对其一些结构细节，如螺栓孔和倒圆角等进行必要的简化后，应用10节点solid 92体单元进行离散化处理，厚度方向单元两至三层，保证计算精度。基于ANSYS平台建立有限元模型，如图1所示，桥壳材料属性如表1所示。板簧座处应用弹簧单元模拟钢板弹簧，采用体单元模拟簧载质量，并利用钢板弹簧的刚度和阻尼特性来定义弹簧单元的参数[5]。

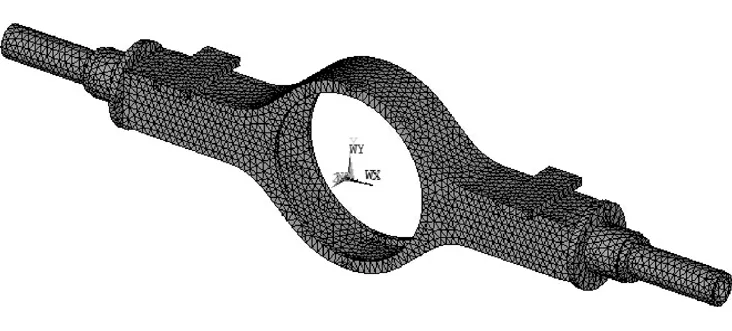
图1 桥壳的有限元振动模型

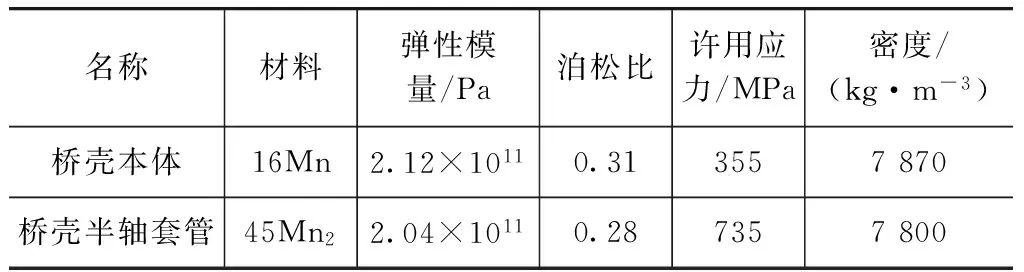
名称材料弹性模量/Pa泊松比许用应力/MPa密度/(kg·m-3)桥壳本体16Mn2.12×10110.313557870桥壳半轴套管45Mn22.04×10110.287357800

1.2 路面随机输入下桥壳载荷激励分析

确定路面随机输入下的桥壳载荷工况是对桥壳可靠性进行分析评估的前提。为此，以GB 18352.3—2005规定的循环工况为基础[6]，如图2所示，对路面随机输入下的桥壳载荷谱进行分析。

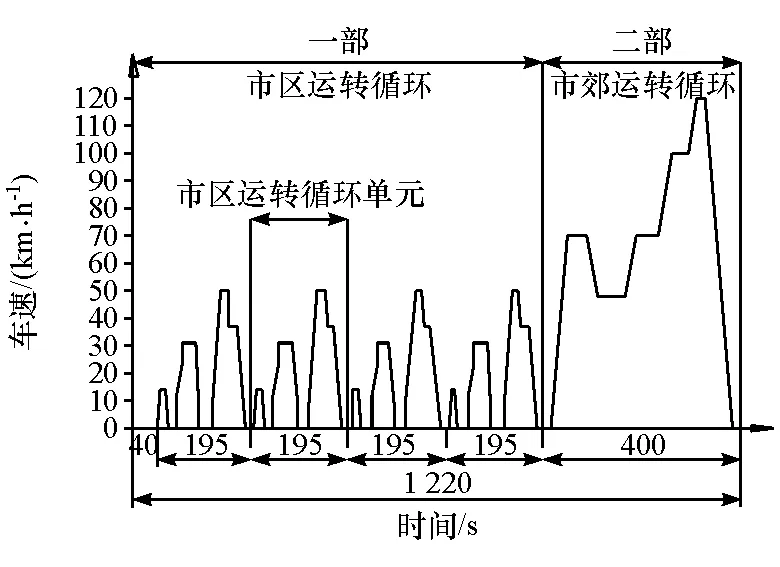
图2 GB 18352.3—2005汽车运转循环图

在上述循环工况下，汽车经历了匀速、加速和制动等多种工况，须要考虑车速对路面随机激励下的桥壳载荷谱的影响。以二部最后一个制动工况为例，车辆制动时桥壳除了受路面和钢板弹簧的垂向载荷作用外，还受到路面传递给桥壳的制动力和扭矩。在掌握相应载荷谱的基础上，可对其进行功率谱密度分析。不失一般性，假定路面速度功率谱密度在整个空间频率范围为白噪声[6]：

(1)

则对应车速为u时，时间域下路面激励速度功率谱密度为

(2)

图3 D级路面车速13.89～19.44m/s时的速度功率谱

图3为D级路面车速13.89～19.44m/s时的速度功率谱。图中，功率谱值随着速度的增加而增大，频率的覆盖范围也相应增大，总体上呈倒梯形，f在0.153～39.3Hz之间图形可近似为矩形，须要将此区域等效为一条直线hb,如图4所示。f在39.3～55Hz之间为三角形，功率谱的值在增大，但相比矩形区域，三角形区域在相同f下所覆盖的功率谱的范围不断减少，即货车所能经历的此功率谱的概率在减小，据此，生成一条功率谱密度值的曲线bg，见图4。

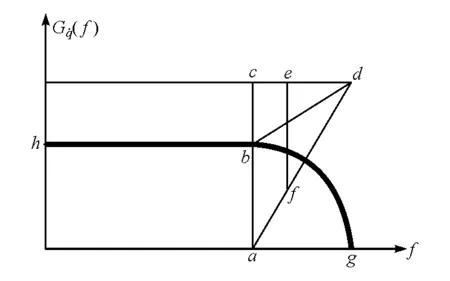
图4 拟合得到功率谱值和频率的关系曲线

假设hb直线段的功率谱密度大小为G′，等效准则为桥壳在此路面功率谱的随机激励作用下造成的疲劳损伤与矩形区域平均作用下的疲劳损伤大小相同，即

D1′+D2′=2D′

(3)

式中:D1′,D2′和D′分别为功率谱在0.005 6，0.007 8m2/s和G′时，在某一定的时间T内对桥壳造成的疲劳损伤。根据疲劳累计损伤准则和材料的S-N曲线得到桥壳在相应功率谱密度激励下产生的应力关系式为

(4)

式中m为材料常数。

0.094

(5)

其中i=1，2

(6)

其中：

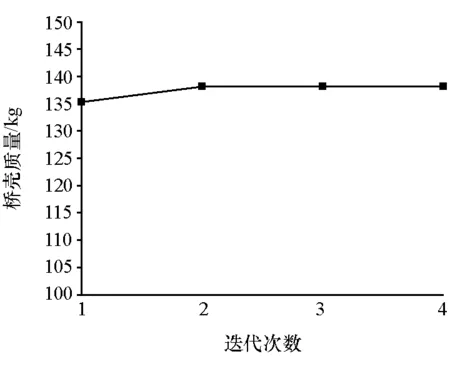
39.3Hz

ys=5.22×10-5f+4.93×10-3

(7)

(8)

式中：ys为bd线段表达式；Def和Dac为ef和ac长度。

将式(7)和式(8)代入式(6)得到图4中bg曲线的方程式：

13.825×10-3

(9)

其中39.3Hz

因此，此时路面速度功率谱密度在0.153Hz

1.3 路面随机输入下桥壳结构动态响应分析

基于ANSYS平台对桥壳在路面随机激励下的响应进行分析。随机振动分析得到的应力具有统计意义。可以假定零件所受的应力服从正态分布，根据3σ准则，应力值在-1σ～1σ之间的概率为68.3%，-2σ～2σ之间的概率为95.4%，-3σ～3σ之间的概率为99.73%。同时考虑到本体和半轴套管材料不同，许用应力也不同，必须同时考虑其损伤情况，考察它们的疲劳可靠性。

仍以加速工况为例，约束和加载条件如表2所示。将上述得到的路面速度功率谱值作为随机输入，作用在两端半轴套管，进行随机振动分析，结果为：桥壳最大应力在半轴套管轴承座部位，1σ值为78.6MPa，应力云图见图5；本体1σ值为51.0MPa，位于减速器安装孔边缘处，应力云图见图6。

表2 桥壳约束和加载条件

图5 桥壳1σ应力云图

图6 本体1σ应力结果云图

2 桥壳疲劳可靠性评估与结构优化

考虑疲劳统计特性，大于3σ应力的概率很小，忽略不计。根据Miner线性累计损伤规律，分别得到-1σ～1σ，-2σ～2σ和-3σ～3σ应力之间实际循环次数n1,n2和n3，再根据S-N曲线得到理论许用循环次数N1,N2和N3，则总体损伤为

(10)

ANSYS默认平均应力为零，幅值在-1σ～1σ之间，而实际工况中桥壳随机振动分析的应力均值为静载分析时的应力值，因此须要对S-N曲线进行修正。

S-N曲线中的疲劳寿命的经验描述是针对疲劳

循环平均应力为零的对称循环疲劳载荷，疲劳理论证明，载荷应力的幅值大小对疲劳损伤起决定性的作用，但是应力均值的影响对疲劳寿命的影响也不能忽略[7]，平均应力越大，寿命越短。

工程上常用GOODMAN公式对应力进行修正[3,8]:

(11)

本文中桥壳本体材料为16Mn,半轴套管材料为45Mn2，基于存活率99%的条件下，S-N曲线拟合公式[9]分别为

logN=29.5020+(-9.5881)logσ

(12)

logN=28.5217+(-8.5901)logσ

(13)

进行优化时，以桥壳的疲劳累积损伤作为约束条件，确保其在最大行驶里程下的疲劳累积损伤小于1。在设计变量的选择上，选取对于桥壳质量和可靠性影响较大的桥壳本体厚度H1、半轴套管厚度H2、减速器孔的半径R1作为优化设计变量。上述设计变量的初始值和取值范围如表3所示。

表3 设计变量的取值 m

根据Miner累计损伤理论，将各工况的疲劳损伤值叠加，可得到在一个工作循环下的本体疲劳损伤d1和半轴套管疲劳损伤d2。由图2可知该循环工况总行驶路程为11 007m，按照国家规定的机动车使用年限和行驶里程，设货车可靠行驶目标里程为60万km，则目标里程下的本体损伤D1=d1×60×107/11007；半轴套管损伤D2=d2×60×107/11007。在不发生疲劳破坏的条件下充分考虑材料的利用率,避免材料浪费，要求0.8

基于上述优化模型，应用1阶优化算法，对桥壳进行优化，原理是利用因变量对设计变量求偏导，找到极小值，目标性更强，收敛速度较快，结果精确。经过4次迭代后达到最优解，如图7和图8所示。优化设计变量的取值和优化结果见表3。

图7 疲劳损伤优化结果

图8 桥壳质量优化结果

由图7和图8可以看出：最初设计方案不满足约束条件，即桥壳本体未到规定里程则发生疲劳破坏；经过优化，半轴套管和本体的疲劳累积损伤分别由8和23降到了0.89和0.92，桥壳本体壁厚略有上升，从原来的14mm增加到14.3mm，半轴套管的外径略有增加，放置减速器孔的半径略有减小，桥壳质量从原来的135kg变为138kg。虽然桥壳的质量略有增加，但是满足疲劳可靠性的优化条件，可确保行驶里程内不发生疲劳破坏，实现了桥壳的优化设计目标。

3 结论

(1) 基于静载荷工况的可靠性评价方法不适用于桥壳的疲劳可靠性评价，而基于循环工况的桥壳疲劳可靠性分析有望对其疲劳可靠性提供更准确的评估。

(2) 桥壳在路面随机激励下的载荷谱是对其进行可靠性分析的重要前提，因此，计入循环工况下车速变化影响的载荷谱分析是对桥壳在循环工况下疲劳可靠性进行分析评估的重要工作内容之一。

(3) 桥壳承受的载荷作用特征对其疲劳可靠性有一定影响，因此，对非对称载荷作用下的桥壳疲劳可靠性分析评价须要对其S-N曲线进行必要的修正。

(4) 基于静力学分析结果的可靠性评价方法已不能满足当前工程实践中桥壳结构优化设计的要求，本文中提出的路面随机输入下对桥壳进行疲劳可靠性分析的方法可为进一步完善桥壳结构的可靠性优化相关工作提供有益的参考。

[1] 陈家瑞.汽车构造[M].北京:机械工业出版社,2000:154-156.

[2] SHAO Y, LIU J, MECHEFSKE C K. Drive Axle Housing Failure Analysis of a Mining Dump Truck Based on the Load Spectrum[J]. Engineering Failure Analysis,2011,18(3):1049-1057.

[3] TOPAC M M, GÜNAL H, KURALAY N S. Fatigue Failure Prediction of a Rear Axle Housing Prototype by Using Finite Element Analysis[J]. Engineering Failure Analysis,2009,16(5):1474-1482.

[4] 高晶,宋健,朱涛.随机载荷作用下汽车驱动桥壳疲劳寿命预估[J].机械强度,2009,30(6):982-987.

[5] 郑燕萍,倪晓宇,方明霞,等.基于随机载荷的汽车驱动桥壳概率疲劳计算[J].南京林业大学学报(自然科学版),2009(9):105-108.

[6] 余志生.汽车理论[M].北京:机械工业出版社,2009:44-210.

[7] 林正祥.汽车驱动桥桥壳动力特性分析与疲劳寿命预测[D].合肥:合肥工业大学,2009.

[8] 惠纪庄,孙德仕,邹亚科.Miner线性累计损伤理论在汽车试验场可靠性试验强化系数研究中的应用[J].工程设计学报,2008,15(4):264-267.

[9] 吴跃成.驱动桥疲劳可靠性分析与试验方法研究[D].杭州:浙江大学,2008.

Fatigue Reliability Analysis on the Driving Axle Housing of aLight Truck Under Random Road Excitation

Lu Jianwei, Wang Xinzi & Wu Weiwei

SchoolofMechanicalandAutomotiveEngineering,HefeiUniversityofTechnology,Hefei230009

The fatigue reliability of driving axle housing under random road excitation is analyzed and optimized in this paper. Firstly a parametric finite element model for the driving axle housing of a light truck is established with ANSYS, the load spectra of axle housing exerted by random road in variable speed conditions is analyzed, and the dynamic responses of the axle housing under road random excitation are obtained. Then on this basis, the cumulative fatigue damage of axle housing under driving cycle conditions is calculated according to Miner cumulative damage criterion, and its fatigue reliability is evaluated. Finally the axle housing is optimized with its fatigue reliability within a certain mileage as constraint. After optimization the fatigue reliability of axle housing is improved, meeting design requirementsn.

axle housing; random road; driving cycles; fatigue; optimization

*教育部新世纪优秀人才支持计划(NCET-10-0358)资助。

原稿收到日期为2014年7月18日，修改稿收到日期为2014年8月27日。