基于自适应遗传算法的模糊伙伴选择

张红

基于自适应遗传算法的模糊伙伴选择

张红

福建船政交通职业学院，福建福州350004

在模糊环境下，引入模糊理论，以具有时序关系的任务时间的最大平均满意度为优化目标，建立项目伙伴选择的数学模型更符合生产实际情况。而利用自适应遗传算法求解可改进基本遗传算法收敛慢的缺点，通过验证这种算法能以更快的速度收敛，达到全局最优值。

伙伴选择；模糊数；自适应遗传算法

一、模糊伙伴选择的提出

在以往的虚拟企业合作伙伴的研究中，大多数学者所考虑的都是在条件精确的下进行的。然而，事实上由于各种不确定因素的存在，如合作伙伴的加工进度的不确定，加工过程中机器的故障，操作工人的熟练程度，因故缺席等，以及运输过程中的不确定因素，这些都造成了开工时间和交货期不能精确，合作伙伴只能够提供一个大概的数据以及数据的范围。因此，我们研究在模糊环境下虚拟企业伙伴选择的问题，引入模糊数学理论来描述候选伙伴的开工时间和交货期的不确定性，研究的模型更接近于实际情况，符合生产要求，更容易被用户接受。

近年来，随着模糊数学的发展，应用模糊数学解决不确定参数问题引起了广泛的关注，有很好的优越性和发展前景。把模糊数学运用到合作伙伴的选择当中，把任务的开工时间和交货期按模糊数学处理更符合实际生产情况，已成为非确定性合作伙伴研究的一个分支。所以，关于模糊开工时间和模糊交货期的研究有重要的意义。

二、模型的建立

在模糊的开工时间、完工时间及交货期下，以极大化平均客户满意度（每一个组合满意度的平均值mean（AI））为目标的虚拟企业合作伙伴选择问题可以描述为如下模型：

约束条件：

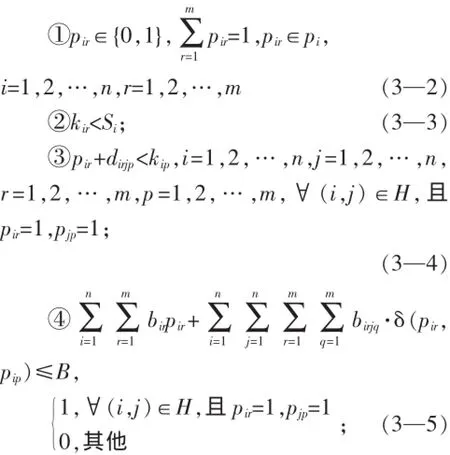
式（3—1）表示极大化平均客户满意度的目标函数；式（3—2）表示每个任务必须从候选伙伴集中选择一个候选伙伴完成，且只能由一个候选伙伴来完成；式（3—3）保证任务的最早允许开工期约束；式（3—4）保证任务的开工期约束；式（3—5）保证项目的成本约束。

在对合作伙伴选择的模型建立后，要构造相应的算法对问题进行优化求解。

三、自适应遗传算法

遗传算法（Genetic Algorithm）是J.Holland在1975年提出的，是基于对自然界中生物遗传与进化理论的仿真，模仿生物进化过程中的“物竞天择，适者生存”的原理，在一定程度上解决了传统的基于符号处理机制的人工智能方法在知识表示、信息处理和解决组合爆炸等方面所遇到的困难，其自组织、自适应、自学习和群体进化能力使其适合于大规模复杂优化问题。遗传算法作为一种实用、高效、鲁棒性强的算法、适用于并行分布处理以及应用范围广的特点。经过20多年的发展，遗传算法已经在函数优化、组合优化、数据挖掘、生产调度、机器学习、图像处理等领域得到成功应用。

基本遗传算法容易出现早熟收敛、易陷入局部极值点的问题，即算法收敛于一个非全局最优点，出现这种问题是一种被称为“顶端优势”的现象存在，即当算法进行到某一代时，在种群中某个个体的适应度值远远大于其他个体的适应度。因为大多数选择策略采用繁殖机会与适应值成比例的方法，这样就会使子代中许多个体来自同一祖先。一旦出现过早收敛，遗传算法中的交叉操作就会失效。从理论上来讲，遗传算法中的变异操作可以使算法跳出局部最优，但是为了保证算法的稳定性，变异操作的变异概率通常取值较小（例如0.01），算法一旦出现过早收敛，靠传统的变异操作需要许多代才能变异出一个不同于其他个体的新个体，因此，本文采用自适应遗传算法，能够有效防止这种问题的出现。

遗传算法的交叉概率和变异概率的选择是影响遗传算法行为和性能的关键参数，直接影响算法的收敛性。在一般的遗传算法中，对所有个体的交叉概率和变异概率选用固定参数，并在遗传过程中保持不变。本文提出了交叉和变异概率的自适应调整规则，使得每个个体按其适应度大小选择不同的交叉概率和变异概率。而且，在遗传过程中根据适应度的变化自动调节这两个控制参数。这样，群体中每个个体对环境的变化就具有了自适应调节能力。

自适应交叉概率设计为：

自适应变异概率设计为：

式中：pc0、pc1分别表示最大的交叉概率和最小的交叉概率；pm0、pm1分别表示最大的变异概率和最小的变异概率；fmax是群体中最大的适应度值；favg是每代群体的平均适应度值；f是要交叉的两个个体中较大的适应度值；f′是要变异个体的适应度值。

四、约束处理

常用的约束处理方法有：搜索空间限定法、可行解变化法、简化约束条件法、惩罚函数法。

惩罚函数因为执行简单而被广泛的应用，它的基本原理是将约束问题中的不等式和等式约束函数经过加权后，和原目标函数结合成新的目标函数，将约束问题转化为无约束问题。

在新目标函数中，r1和r2是惩罚因子，项，障碍项的作用是当迭代点在可行区域内时，在迭代的过程中阻止迭代点越出可行域，惩罚项的作用是当迭代点在非可行域或不满足约束条件时，在迭代过程中将迫使迭代点逼近约束边界或等式约束曲面。

但是使用惩罚函数处理约束，会产生以下问题：（1）惩罚因子难以确定，解决问题的好坏取决于选择惩罚因子的好坏；（2）问题的可行域较小，个体跳出可行域的机会较大。

为了更好的处理约束问题，Jimenez和Verdegay提出了一种联赛选择算法，并采用以下比较准则进行比较：

1．当两个个体都是可行解时，目标函数值较小的占优；

2．当两个个体，一个是可行解，另外一个是不可行解，可行解总是优于不可行解；

3．当两个个体都是不可行解时，则违反约束较小的总是占优。

基于以上3个原则，苏平（2006）构造了一种不需要设置惩罚因子的约束处理方法，取得了较好的效果。该方法的思想用于遗传算法中处理约束，定义满足所有约束条件的粒子为可行粒子，否则称之为不可行粒子，一旦违背了约束条件，可行粒子变为不可行粒子。

根据本实例的特点，目标函数是平均值的最大值，根据约束条件判断粒子是否是可行解，当粒子满足所有约束条件时，粒子的适应度不变，保留较好粒子个体，粒子逐渐靠近最优解。当粒子没有满足所有的约束，粒子的适应度增加惩罚约束函数P（x），P（x）为足够大负值，使得粒子的适应度比满足所有约束条件的粒子要小，这样使这些粒子保留下来的概率较小。采用以下式子计算适应度：

其中，fmin（x）为最差可行解适应度，即最小适应度，P（x）为惩罚函数。

五、实例应用

以模具制造为例，一个模具制造企业需完成一个大型注塑模的项目，由于该企业不具备完成这个项目的所有资源，故需要组织虚拟企业来完成。该项目分解成下列制造任务：

任务1：产品的三维造型、模具设计，包括型腔、型芯和电极的设计，需要有经验的模具设计人员和相关的CAD软件包。

任务2：模架的设计、模架制造工艺设计、模架加工制造以及在模架上进行相关加工，需要大型铣床和磨床。

任务3：型腔和型芯的工艺设计、NC编程及镶块的粗加工，需要数控机床。

任务4：电极的工艺设计、NC编程和加工，需要精密数控机床。

任务5：镶块的电火花加工，需要电火花机床。

任务6：其他零部件的设计和制造、模具装配，需要有经验的模具工人。

任务7：试模，需要大型注塑机。

任务8：根据试模结果进行修模，需要有经验的模具工人。

任务之间的先后次序关系如图所示。企业决定任务1由自己完成，其他的任务由合作伙伴来完成。经过初选，任务2～7有3个候选伙伴，任务8有2个候选伙伴。根据各候选伙伴的地理位置关系、需要运送的材料和运输工具，可以估算出其费用和时间。需要项目的成本预算是70w，模糊交货期为（39，39.5，41.5，42）。

图3-1任务的先后顺序关系

表3-1候选伙伴费用数据表

候选伙伴费用数据如表3-1所示：

候选伙伴的时间数据如表3-2所示：

遗传算法的参数为：种群大小N＝200，交叉概率pc＝0.7，变异概率pm＝0.1，最大进化代数T＝50。

自适应遗传算法的参数设置：种群大小N＝200，交叉概率：最大交叉概率pc0=0.9，最小交叉概率pc1=0.6，变异概率：最大变异概率pm0=0.1，最小变异概率pm1=0.001，最大进化代数T=50。

分别采用遗传算法和自适应遗传算法搜索结果，Matlab仿真结果为：

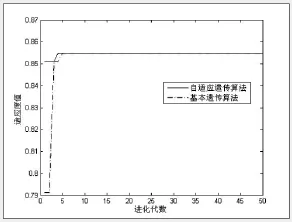
图3-2遗传算法搜索结果

利用基本遗传算法仿真，求得极大化平均客户满意度的解为[1 1 2 3 1 3 3 1]，即合作伙伴的最优组合为：{p11，p21，p32，p43，p51，p63，p73，p81}，交货期的满意度为100%，极大化平均客户满意度为：85.5%，所需要的成本为：67.4w。

采用遗传算法进行优化得到的任务对的满意度如下表3-3所示：

利用自适应遗传算法仿真，求得极大化平均客户满意度的解为[1 1 2 3 1 3 3 1]，即合作伙伴的最优组合为：{p11，p21，p32，p43，p51，p63，p73，p81}，交货期的满意度为100%，极大化平均客户满意度为：85.5%，所需要的成本为：67.4w。

表3-3任务对的满意度

采用自适应遗传算法优化得到的任务对的满意度如下表3-4所示：

表3-4任务对的满意度

从搜索结果可以得出：

1．遗传算法和自适应遗传算法都能达到全局最优值。

2．在搜索速度方面，自适应遗传算法能够以更快的速度收敛，达到全局最优值。

[1]MaCahon C,S,Lee.E.S.Fuzzy Job Sequencing for Flow Ship[J].European Journal of Operational Research,1992，62：294-301.

[2]Fortemps.P.Job Shop Scheduling with Impecise Durations:A Fuzzy Approach[J].IEE-E Trans on Fuzzy Systems,1997，5（4）：557-569.

[3]王凌.车间调度及其遗传算法[M].北京：清华大学出版社，2003：146-153.

[4]袁晓辉，王乘，张勇传，等.水电系统短期经济运行的新方法[J].水力发电学报，2006（4）：1-5.

[5]苏平，伍乃骐，于兆勤，等.改进遗传算法在虚拟企业伙伴选择与优化中的应用[J].系统工程理论与实践，2006（12）：85-92.

责任编辑：陈卓陈岩

Fuzzy Partner Selection Based on Adaptive Genetic Algorithm

ZHANG Hong
（Fujian Chuanzheng Communications College,Fuzhou Fujian 350004）

The fuzzy theory is introduced in an obscure environment.The maximum average satisfaction of the task with a sequential relationship is taken as the optimization goal.The mathematic model of project partner selection is more in line with the actual production situation.The adaptive genetic algorithm(GA)is used to improve the convergence speed of the basic genetic algorithm,thus, the global optimal value and a faster convergence speed can be obtained by verifying the algorithm.

partner selection;fuzzy number;adaptive genetic algorithm

TP18

A

2095－5537（2016）06－00073－05

2016-09-30

张红（1969—），女，汉族，湖南省湘潭人，福建船政交通职业学院高级实验师。研究方向：计算机应用技术、电教。