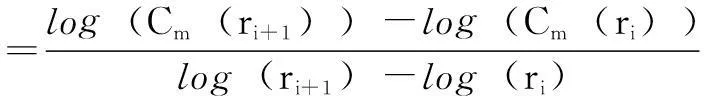实测铁磁谐振时间序列的非线性动力学分析

黄艳玲　司马文霞　杨　鸣　杨　庆　袁　涛

(输配电装备及系统安全与新技术国家重点实验室(重庆大学)　重庆　400044)



实测铁磁谐振时间序列的非线性动力学分析

黄艳玲司马文霞杨鸣杨庆袁涛

(输配电装备及系统安全与新技术国家重点实验室(重庆大学)重庆400044)

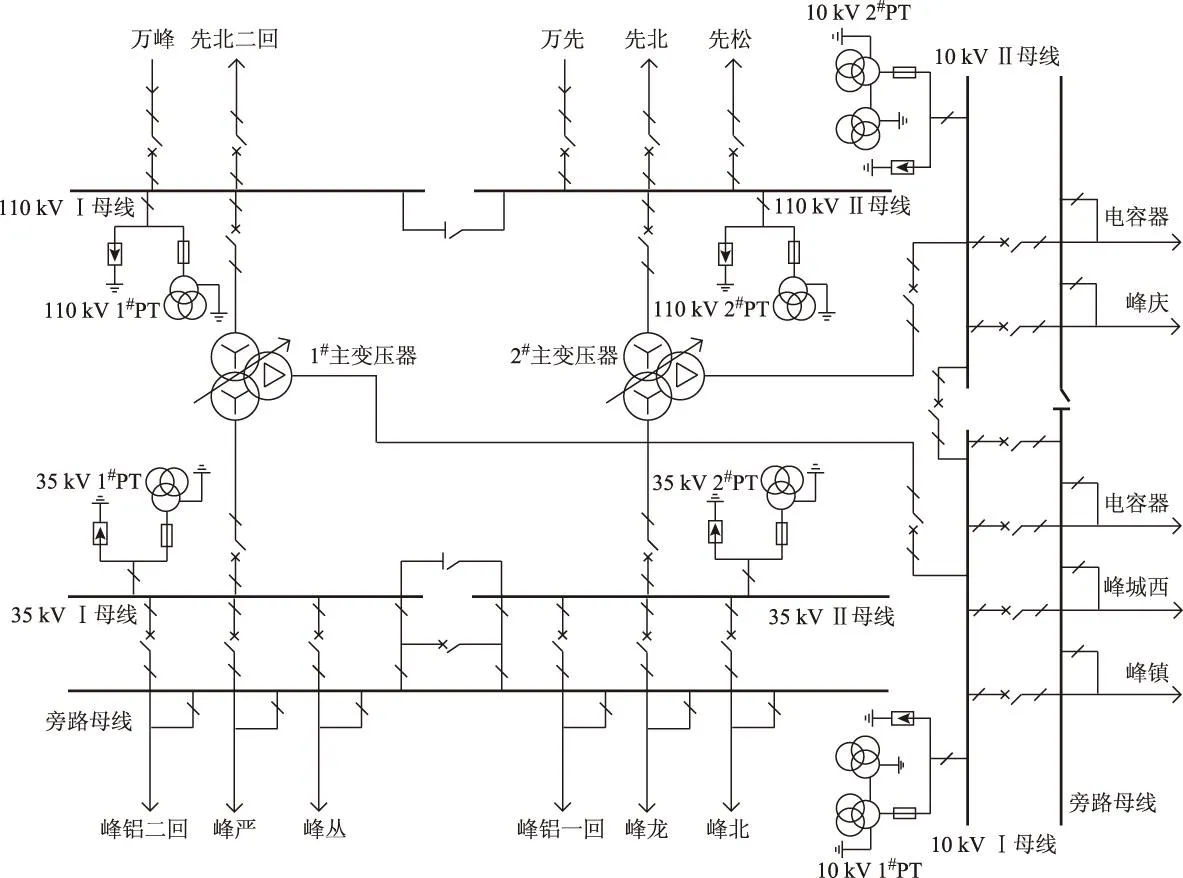
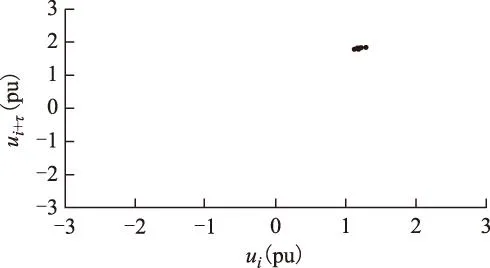
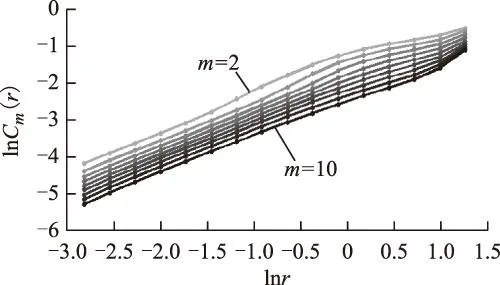
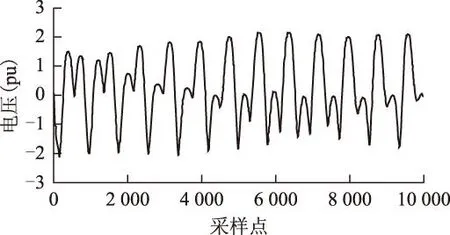
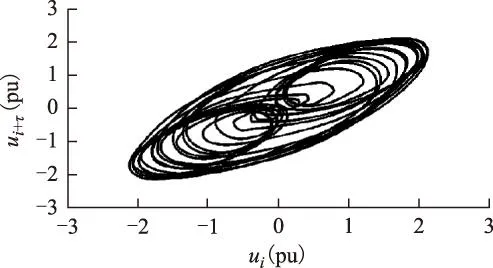
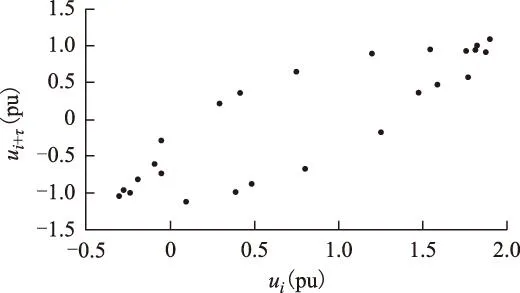
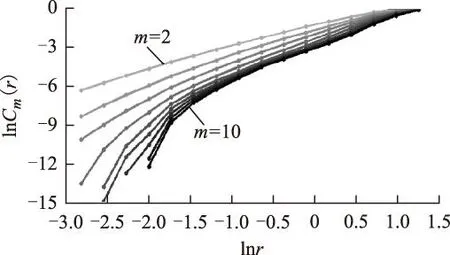
摘要在仅有实测单一电压时间序列的情况下，为准确识别出电力系统铁磁谐振类型，运用坐标延迟方法重构与原系统拓扑意义上等价的相空间。采用相平面、庞加莱截面和关联维数3种基于重构相空间的非线性动力学分析工具表达电压时间序列的运动特征，由此识别其所属的铁磁谐振类型。对3例典型的中性点不接地系统电磁式电压互感器铁磁谐振实测时间序列进行了动力学特征分析。其中两例时间序列的相平面轨迹、庞加莱截面均呈现周期运动特性，关联维数估计值分别为1.015 0±0.003 9、1.006 1±0.000 6，由此判别它们作周期运动；另一例时间序列的相平面轨迹、庞加莱截面均未呈现周期或准周期运动特性，关联维数估计值为2.300 2±0.061 2，由此判别其作混沌运动。实测电压时间序列受到多种因素的影响，综合以上3种分析方法所表达的特征，对所发生的铁磁谐振类型作出的判断更准确和更有说服力。

关键词：铁磁谐振时间序列非线动力学相空间重构关联维数电磁式电压互感器

Nonlinear Dynamic Analysis of the Measured Ferroresonance Time Series

HuangYanlingSimaWenxiaYangMingYangQingYuanTao

(State Key Laboratory of Power Transmission Equipment and System Safety and New Technology Chongqing UniversityChongqing400044China)

AbstractWith only a single voltage time series recorded in fact，for accurately identifying the ferroresonance types，the delay coordinates method was applied to obtain the reconstructed phase space that is topologically equivalent to the phase space of the original system.Nonlinear dynamics methods based on the reconstructed phase space，e.g.phase plane，Poincaré section and correlation dimension，were used to express the dynamic characteristics of the time series and identify the type of ferroresonance based on them.The nonlinear dynamic characteristics analysis was conducted to 3 typical cases of measured time series of ferroresonance occurred in inductive voltage transformer in isolated neutral system.The phase plane trajectories and Poincaré sections of two time series cases of them show periodic motion characteristics，their correlation dimension estimation values respectively are 1.015 0±0.003 9，1.006 1±0.000 6；therefore their motion modes were identified as fundamental mode and subharmonic mode.The phase plane trajectory and Poincaré section of another time series case do not show periodic or quasiperiodic motion characteristics，its correlation dimension estimation value is 2.300 2±0.061 2；therefore its motion mode was identified as chaotic mode.The measured voltage time series is affected by many factors，the identification result of ferroresonance mode occurred is more accurate and convictive through synthesizing the features characterized by the above 3 analysis methods.

Keywords：Ferroresonance，time series，nonlinear dynamics，phase space construction，correlation dimension，inductive voltage transformer

0引言

铁磁谐振是一种复杂的电现象，它可能发生在由电力变压器或电磁式电压互感器(PT)及带铁心的电抗器等非线性电感元件与电容元件构成的回路中[1]。非线性电感元件的饱和励磁特性使铁磁谐振行为呈现非线性动力学特性，其稳态响应模式高度依赖于系统参数和初始条件，初始条件稍有变化就可能使响应模式发生改变[2]。稳态响应模式可能是周期、准周期或混沌模式。在合适的条件组合下，很多设备操作行为及单相接地故障消除瞬间[3]均可能激发铁磁谐振，由此产生的过电压或过电流严重危害着变电站设备的绝缘，甚至造成变压器或PT的烧毁，继而引发大面积的停电事故。因此，当铁磁谐振发生时，很有必要识别出谐振类型，为采取有效的过电压抑制措施和电网事故分析提供指导。这对保障电网的安全运行具有重要意义。

常规的线性数学方法不适于分析非线性的铁磁谐振行为，Z.Emin和其他学者将基于相空间的非线性动力学分析工具相平面[1，2，4，5，10]、庞加莱截面[1，2，4-10]和Lyapunov指数[4，8，10]等运用到铁磁谐振行为的特征分析和识别中，再结合功率谱密度分析[1，6，9]对识别结果进行验证。在此基础上，为进一步获取系统发生谐振的参数取值范围以及谐振类型，基于分岔理论的分岔图[2，5，8，9]被用于预测系统随某一参量变化可能出现的谐振类型。

尽管基于相空间的非线性动力学分析工具对铁磁谐振行为的特征分析和识别取得了很好的效果，但当前所研究的铁磁谐振数据主要是通过建立谐振回路的微分方程组进行数值求解[1，4，6-10]或是应用ATP-EMTP软件搭建回路仿真[5]所得，与实际情况有一定的差距。因建立的数学仿真模型是系统结构的简化表达，铁心损耗及系统对地电容等系统参数难以准确获取，尤其对电感元件的非线性特性模拟的精度有待提高。只有对正在发生的铁磁谐振类型进行识别，才能为制定合适的过电压抑制策略提供帮助，但实际观测和获取的常常只是铁磁谐振系统单一状态变量(如电压的时间序列)，而以上基于相空间的研究方法[1，2，4-10]至少需要两个状态变量的时间序列数据，因此需要借助其他方法先构造相空间。

因一个变量随时间的变化隐含了整个系统的运动规律，根据F.Takens提出的嵌入定理[11]，从一维时间序列可重构一个与原动力系统在拓扑意义上等价的相空间。因此，可对单一变量的时间序列运用相空间重构方法构造相空间，通过分析重构相空间轨线的分布或结构得到原系统的动力学特征。

本文在仅有某一中性点不接地系统PT铁磁谐振实测电压时间序列的情况下，运用相空间重构方法获得系统相空间。在此基础上，运用相平面、庞加莱截面和关联维数3种基于相空间重构的非线性动力学分析工具表达系统的动力学特征，以识别铁磁谐振类型。

1非线性动力学分析方法

1.1相空间重构

系统相空间是由状态变量xi(i=1,2,…,n)张成的空间Rn， 相空间的一个点对应系统的一个状态。N.H.Parkard等[12]于1980年提出了基于单一变量时间序列的两种相空间重构方法：导数重构法和坐标延迟重构法。因实测数据混有噪声，对其求取的微分误差较大，因此实际应用中主要使用坐标延迟重构法进行一维时间序列的相空间重构。

1.1.1坐标延迟重构法

设有一单变量的时间序列u={ui|i=1,2,…,N}， 对于某一给定的嵌入维数m和延迟时间τ，其相空间向量序列为

V={Vk|uk,uk+τ,…,uk+(m-1)τ}

(1)

式中，k=1,2,…,n；n=N-(m-1)τ。

由此，重构相空间的轨线分布或结构便反映了系统的运动特征。将重构相空间的某两个向量的取值序列分别作为横、纵坐标绘制在平面中就构成重构相平面。系统作周期运动时，其相平面轨迹是一条不断重复的闭合曲线[2]；而作混沌运动时，相平面轨迹永不重复[1]。

1.1.2坐标延迟重构参数选取

坐标延迟重构法参数即延迟时间τ和嵌入维数m的选取很关键。当前对它们的选取有两种观点[13]，一种观点认为二者互不相关，对τ和m的选取可独立进行，分别有不同的确定方法。最佳τ值的求取方法主要有自相关函数法[14]和互信息法[15]。最佳m值的估计方法有计算吸引子不变量法(或G-P法)[16]、奇异值分解法[17]、伪最近邻法[18]和伪最近邻Cao氏改进法[19]。另一种观点认为τ和m相互关联，即τ和m的关系与重构相空间的嵌入窗τw(τw=(m-1)τ)密切相关。D.Kugiurmtzis[20]于1996年首次提出嵌入窗思想，基于嵌入窗思想的典型算法有C-C法[21]和自动嵌入式相空间重构法[22]。

本文在确定相空间重构参数时采用第一种观点，即τ和m的值采用不同的方法确定。采用互信息法获取最佳τ值，因互信息刻画的是两个变量间的普遍(或总体)相关性，适用于非线性系统。本文采用的计算过程无需事先确定最优m值，但通过计算一组m值下的关联维数可间接获取最优m值(即G-P法确定最优m值，实现方法见1.3.1节)。

1.2庞加莱截面

庞加莱截面是相平面轨迹的一种简化表达，是对相平面轨迹以一定的频率采样获取的相点图。

若对相平面轨迹采样的频率为系统外加激励函数的频率(如电源频率)，则对作周期运动的系统，在庞加莱截面上表现为一个不动点或是多个孤立点[1]；对作准周期运动的系统，庞加莱截面是一条分布着无限个不同点的封闭曲线[6，7]；而当系统作混沌运动时，庞加莱截面呈现为局限于平面某一特定区域的一些随机分布的相点集合[1]。

1.3关联维数

判断一个时间序列是否具有混沌特性最为常用的动态不变量有Lyapunov指数[4，8，23]和吸引子维数[7，23]。由于实验获取的时间序列数据ui受到多种因素(如采样精度、采样长度、噪声和误差等)的影响，仅凭其最大Lyapunov指数λmax的正负就对系统的运动特性作出判断，很可能不准确[24]。自1983年P.Grassberger等[25]提出针对一维时间序列数据的关联维数计算方法(简称G-P算法)后，关联维数作为吸引子维数的一种度量得到了广泛应用。本文采用关联维数作为判别系统混沌特性的动态不变量。

1.3.1关联维数G-P算法

给定一尺度r和嵌入维数m，定义相空间距离小于r的点对数与所有点对数的比例为关联积分Cm(r)，即

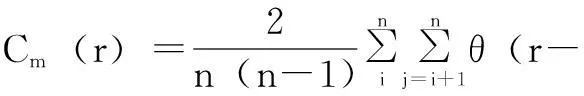
(2)

式中，n为相空间的点数；‖·‖表示求两个重构向量的欧氏范数；θ(x)为Heaviside阶跃函数。

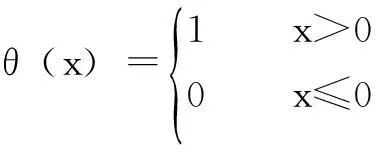
(3)

对于无限长序列(n→∞)和足够小的r值，若Cm(r)与r呈幂律关系，即Cm(r)∝rD2， 则定义关联维数D2为

(4)

实际所获取的数据量有限，无法满足极限条件n→∞， 而且尺度r的取值须满足式(5)。

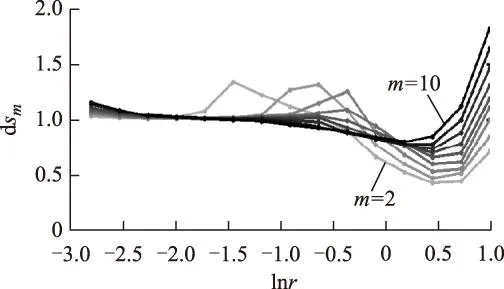
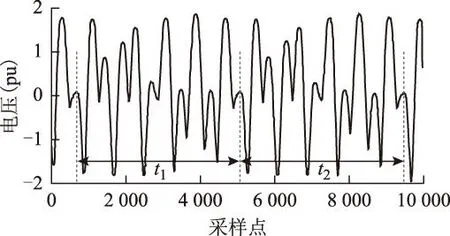
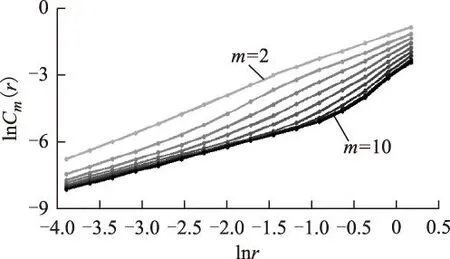
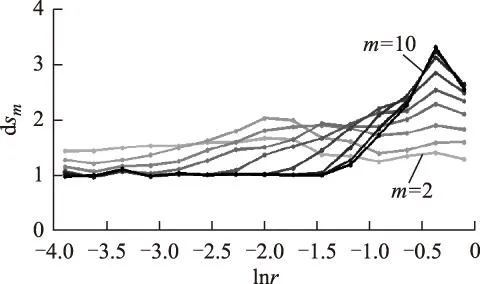
min{‖Vi-Vj‖}

(5)

式中，i≠j，i,j=1,2,…,n。

因此，计算关联维数采取的常规步骤为：

1)在式(5)的范围内取一尺度序列ri(i=1,2,…,l)，计算与ri对应的关联积分序列Cm(ri)。

2)求出序列Cm(ri)和ri的对数序列lnCm(r)i和lnri，以序列lnri为横坐标、序列lnCm(r)i为纵坐标绘制双对数曲线。

3)将双对数曲线线性区(或无标度区)的斜率作为D2的估计值。

因双对数曲线或多或少呈现S形，很难通过目测或经验确定其线性区域。文献[26]指出一个可信的无标度区必须是清晰可辨的，表现在lnCm(r)对lnr曲线的局部斜率dsm对lnr曲线存在随m增大而趋于饱和的平坦区域。

为使估算所得D2尽量准确，本文计算关联维数采取的步骤与常规的不同之处为：

1)计算一组m(m=2~10)的对数序列lnCm(r)i。

2)分别求出m=2～10下lnCm(r)对lnr曲线的局部斜率dsm。

3)若dsm对lnr曲线存在随m值增大而趋于饱和的平坦区域，则将各m值下dsm对lnr曲线的平坦区域作为无标度区，并将此区域对应的数据点对(lnCm(r)，lnr)进行直线拟合得到序列D2_m，由此获取D2估计值。同时，D2_m趋于饱和时对应的m值可作为该时间序列重构的最优m值，即G-P法确定最优m值。

局部斜率dsm的计算式为

(6)

式中，i=1,2,…,l-1。

对于随机过程的时间序列，其D2随m的增大而增大，不会趋于饱和；而确定性系统的D2随m的增大而逐渐趋于饱和。不同的D2饱和值对应于不同的系统运动状态[27]：D2=1，系统作周期运动；D2=2，系统作准周期或拟周期运动；D2>2或D2不为整数，系统作混沌运动。

1.3.2关联维数G-P优化算法

对于长度为n的数据集，在所有的点对中直接搜寻距离小于r的点对所需的计算量为O(n2/2)。如果需要在多个嵌入维下估算D2，则计算耗时还要增加。由于在估算D2时，只有相空间的邻近点对对Cm(r)值有贡献。因此，如果事先大致确定每个相点的近邻分布位置，可大大缩短搜索邻近点对的耗时。基于以上思想，文献[28-30]先后提出采用盒子网格的方法帮助寻找距离小于r的邻近点对。文献[30]提出的基于直方图的盒子辅助(box-assisted)近邻搜索算法，解决了将相空间的点放入盒子而不浪费存储空间的技术难题，而且易于实现。本文应用这一算法计算Cm(r)。

2典型铁磁谐振时间序列的非线性动力学分析

图1　重庆市先锋变电站一次主接线简图Fig.1　Primary wiring simplified diagram of Xianfeng substation in Chongqing city

本文所研究的铁磁谐振时间序列是重庆市先锋变电站的实测数据。该变电站的一次主接线简图如图1所示，图中‘/’表示隔离开关或接地刀开关。该站有两台3绕组变压器，绕组接线方式为YN/yn0/d11，电压等级为110 kV/35 kV/10 kV，35 kV侧中性点不接地。为监视母线绝缘，各电压等级的Ⅰ、Ⅱ段母线均安装有PT。为实现对该站3个电压等级的过电压监测，分别在10 kV开关柜母线，35 kV户外开关场母线，2#主变压器套管110 kV侧安装了电压传感器[31]。自2006年11月16日开始实施对10 kV系统Ⅰ、Ⅱ段母线和2#主变压器110 kV系统的过电压监测，自2008年6月23日开始实施对35 kV系统Ⅰ、Ⅱ段母线的过电压监测。10 kV Ⅱ段母线和35 kV Ⅰ段母线上均监测到铁磁谐振过电压，本文选取具有代表性的铁磁谐振电压序列数据进行特征分析，为进一步研究其分类识别方法奠定基础。

本文对原始采集数据进行了下采样处理和滤波去噪。①下采样。原始数据的采样频率为200 kHz，对于铁磁谐振的稳态过程而言过高，因其所含成分的最高频率不大于1 kHz。为使被分析的数据展现电压变量更多的变化规律，又不使计算量过大，对原始数据采取整数倍抽取的方式获得待分析的时间序列。抽取倍数的确定原则为：最低抽取频率设为10 kHz，抽取频率必须为50 Hz的整数倍，抽取后的相平面轨迹与未抽取前的一致。因此，本文采用实验法确定合适的抽取倍数：以抽取倍数的取值范围2、4、5、8、10、16、20依次进行抽取，并对比抽取前、后的相平面轨迹，若发现有明显差异，则将前一次采用的抽取倍数作为最终的信号抽取倍数。②滤波去噪。因实测数据不可避免地含有噪音，对下采样处理所得的时间序列采用sym8小波5层启发式阈值估计法去噪。

1)时间序列1

时间序列1是2007年2月14日02∶05∶41于10 kV Ⅱ段母线处采集的A相原始数据进行5倍抽取和滤波处理所得的数据，数据长度为10 000。

图2和图3分别为时间序列1的波形图和重构相平面图(N=10 000，τ=26)。图2呈现明显的周期性，过电压幅值达2.802 6 (pu)。图3所示的相平面轨迹是一条近似椭圆形的封闭曲线，表明时间序列1作周期运动。图4为对应于图3的庞加莱截面，采样频率为电源频率。本文中如不作特别说明，对相平面轨迹采样的频率均与电源频率相同。图4中的相点几乎重合，可近似为一个孤立点，表明时间序列1作基频周期运动，频率与电源频率相同。

图2　时间序列1的波形图Fig.2　Waveform plot of time series 1

图3　时间序列1的重构相平面图Fig.3　Reconstructed phase plane plot of time series 1

图4　时间序列1的庞加莱截面Fig.4　Poincaré section of time series 1

图5为时间序列1的lnCm(r)对lnr双对数曲线图，图6为对应于图5的dsm对lnr曲线图。图5和图6中颜色由浅到深的线条分别表示m=2、3、…、10下的相应曲线，后文类似图形中各线条的含义与此相同。尺度r的取值序列为：ri=0.06×1.311 6i-1，i=1,2,…,16。 由图5可知，各条lnCm(r)对lnr曲线的下半部分线性度较好，且在lnr取值区间[-2.270 9，-1.185 9]，m=3～10的lnCm(r)对lnr曲线基本平行。在图6中可观察到各条dsm对lnr曲线均存在清晰的平坦区域，且在lnr取值区间[-2.270 9，-1.475 2]，m=3～10的dsm对lnr曲线基本重合。

图5　时间序列1的lnCm(r)对lnr曲线Fig.5　Curves lnCm(r) versus lnr of time series 1

图6　时间序列1的dsm对lnr曲线Fig.6　Curves dsm versus lnr of time series 1

m=2～10时，D2_m分别为1.024 3、1.013 3、1.017 5、1.018 9、1.018 8、1.017 0、1.017 4、1.013 6、1.012 2。m≥3时，D2_m趋于稳定，由此估算所得D2=1.015 0±0.003 9。该序列重构所需的最小嵌入维数为3。

时间序列1的D2相对于整数1的误差低于2%，非常小，因此其D2理论值应为整数1，作周期运动。这与从相平面轨迹和庞加莱截面得出的结论一致。

对与时间序列1同一时间同一位置获取的B相、C相数据也进行了动力学特征分析，其运动模式与时间序列1的相同，D2分别为1.007 6±0.008 7，1.028 8±0.011 5。

根据识别结果可知，2007年2月14日 02∶05∶41于10 kV Ⅱ段母线监测的铁磁谐振类型是基频周期谐振，其过电压幅值为2.802 6(pu)，一般是不危险的，但若持续时间长，可能导致PT绝缘破坏，甚至烧毁或避雷器爆炸。

2)时间序列2

时间序列2是2009年7月16 日21∶52∶26于35 kV Ⅰ段母线处采集的A相原始数据进行10倍抽取和滤波处理所得的数据，数据长度为10 000。

图7和图8分别为时间序列2的波形图和重构相平面图(N=10 000，τ=44)。从图7可知，t2内的电压取值与t1内的基本相同，t2之后的电压值也有重复的迹象，可初步断定时间序列2具有周期性。t1和t2内有4 400个采样点，t1=t2=220 ms(采样频率为20 kHz)。过电压幅值为-1.876 2 (pu)。图8所示的相平面轨迹是一条由多条轨道组成的封闭曲线，不同的轨道之间有交点。这些特征表明时间序列2作周期运动，其周期比较长。

图7　时间序列2的波形图Fig.7　Waveform plot of time series 2

图8　时间序列2的重构相平面图Fig.8　Reconstructed phase plane plot of time series 2

图9　时间序列2的庞加莱截面Fig.9　Poincaré section of time series 2

与图8对应的庞加莱截面如图9所示。经仔细分析发现，最早出现在庞加莱截面上的11个相点呈离散分布，但分布在庞加莱截面次对角线两端的相点相距较近。此时仅凭图9难以判断时间序列2的运动性质。此后获取的相点依次分布在原11个相点的附近，甚至与原有相点重合。如果时间序列长度为4 400(11个工频周期)的整数倍，则这11个相点分布区域包含的相点数相同。结合相平面轨迹的分析结论，可断定这11个相点区域分别表示11个孤立的离散点(用不同的标记表示)。这表明时间序列2作分频周期运动，其频率为工频的1/11。受测量误差的影响，11个孤立离散区域处相点的分散性不同。

对时间序列1和2的分析表明，测量误差的存在导致庞加莱截面上应重叠的相点未完全重叠，给分析带来困难。因此，对周期比较长的时间序列，运用庞加莱截面时需非常谨慎，时间序列数据要足够长，至少要包含2个运动周期。

图10为时间序列2的lnCm(r)对lnr双对数曲线图。尺度r的取值序列为：ri=0.06×1.311 6i-5，i=1,2,…,16。 从图10可知，m=2～5时lnCm(r)对lnr曲线的形状差异较大，m≥6时lnCm(r)对lnr曲线的形状逐渐一致，且m=9与m=10的基本重合。与图10相对应的dsm对lnr曲线图如图11所示。从图11可观察到，m≥6时dsm对lnr曲线均存在明显的平坦区域，且在lnr取值区间[-3.084 7，-2.270 9]，dsm对lnr曲线平坦且基本重合。

图10　时间序列2的lnCm(r)对lnr曲线Fig.10　Curves lnCm(r) versus lnr of time series 2

图11　时间序列2的dsm对lnr曲线Fig.11　Curves dsm versus lnr of time series 2

m=6~10时，D2_m分别为1.006 3、1.006 7、1.006 7、1.005 7、1.005 6，波动极小，由此估算可得D2=1.006 1±0.000 6。该序列重构所需的最小嵌入维数为6。

时间序列2的D2相对于整数1的误差低于0.7%，非常小，因此其D2理论值应为整数1，作周期运动。这与从相平面轨迹和庞加莱截面得出的结论一致。

对与时间序列2同一时间同一位置获取的B相、C相数据也进行了动力学特征分析，其运动模式与时间序列2的相同，D2分别为1.001 3±0.001 0，1.018 4±0.005 3。

根据识别结果可知，2009年7月16日21∶52∶26于35 kV Ⅰ段母线监测的铁磁谐振类型是分频周期谐振，过电压幅值为-1.876 2 (pu)，电压本身是不危险的，但分频引起的PT过饱和电流，若长时间持续，易导致PT高压熔丝熔断，或引起PT因严重过热而烧毁，甚至爆炸。

3)时间序列3

时间序列3是2009年4月18日01∶29∶58于35 kV Ⅰ段母线处采集的A相原始数据进行10倍抽取和滤波处理所得的数据，数据长度为10 000。

图12和图13分别为时间序列3的波形图和重构相平面图(N=10 000，τ=57)。时间序列3的各波峰之间呈现此消彼长的现象，有一定的重复性，但又不完全重复。过电压幅值为-2.127 5 (pu)。图13呈现的相平面轨迹不是一条封闭曲线，但相点的运动轨道被限制在一个固定的区域，即其运动轨迹并不是无限制扩散和完全杂乱无章。这些特征表明时间序列3不是作周期运动，也不是作随机运动。

图12　时间序列3的波形图Fig.12　Waveform plot of time series 3

图13　时间序列3的重构相平面图Fig.13　Reconstructed phase plane plot of time series 3

与图13对应的庞加莱截面如图14所示。图14的相点呈不均匀的离散分布，未形成一条近似闭曲线，这表明时间序列3不是作准周期运动。因图14中的相点数较少，未呈现自相似的分层结构，因此不能判断时间序列3是否作混沌运动。

图14　时间序列3的庞加莱截面Fig.14　Poincaré section of time series 3

时间序列3的lnCm(r)对lnr双对数曲线图如图15所示，对应于图15的dsm对lnr曲线图如图16所示。尺度r的取值序列为：ri=0.06×1.3116i-1，i=1,2,…,16。 从图15可知，在lnr取值区间[-0.643 4，0.170 3]，双对数曲线随m的增大而逐渐平行，即斜率值逐渐达到饱和。相应地，在图16中可清晰的观察到dsm对lnr曲线存在随m的增大而逐渐饱和的平坦区域，且m=8～10时dsm对lnr曲线的平坦区域基本重合。

图15　时间序列3的lnCm(r)对lnr曲线Fig.15　Curves lnCm(r) versus lnr of time series 3

图16　时间序列3的dsm对lnr曲线Fig.16　Curves dsm versus lnr of time series 3

m=2～10时，D2_m分别为1.678 4、1.837 0、2.118 5、2.341 2、2.361 4、2.264 4、2.238 9、2.302 4、2.312 1。m≥5时，D2_m趋于稳定，由此估算可得D2=2.300 2±0.061 2。该序列重构所需的最小嵌入维数为5。

时间序列3的D2>2，不为整数，且小数部分较大(>0.230 0)，表明其具有混沌运动特性。从庞加莱截面得出的其不是作准周期运动的判断，可验证这一结论。

对与时间序列3同一时间同一位置获取的B相、C相数据也进行了动力学特征分析，其运动模式与时间序列3的相同，D2分别为2.223 6±0.043 6，2.408 3±0.082 4。

根据识别结果可知，2009年4月18日01∶29∶58于35 kV Ⅰ段母线监测的铁磁谐振类型是混沌谐振，其过电压幅值仅稍微超过2 (pu)，电压本身也是不危险的。对时间序列3的频谱分析得知，其含24 Hz频率分量的幅值达1.161 4 (pu)，即含较大幅值的分次谐波。因此，若长时间持续，有与分频谐振类似的危害。

3结论

1)为准确识别实测铁磁谐振一维电压时间序列所属的谐振类型，本文运用相空间重构方法构造系统相空间。在此基础上，采用相平面、庞加莱截面和关联维数3种非线性动力学分析方法，以不同的形式表达其动力学特征，由此对其所属的铁磁谐振类型作出了准确判断。

2)对3例典型的中性点不接地系统PT铁磁谐振实测时间序列进行了动力学特征分析。其中两例时间序列的相平面轨迹、庞加莱截面均呈现周期运动特性，关联维数估计值分别为1.015 0±0.003 9、1.006 1±0.000 6，由此判断它们作周期运动。另一例时间序列的相平面轨迹、庞加莱截面均未呈现周期或准周期运动特性，关联维数估计值为2.300 2±0.061 2，由此判断其作混沌运动。

3)鉴于实测电压时间序列数据受到多种因素(如采样精度、噪音和误差等)的影响，庞加莱截面和关联维数估计值与理想情况有一定差距，要对其运动特性作出准确判断，有必要综合多种方法所表达的特征。

4)中性点不接地系统PT铁磁谐振属于零序性质，发生铁磁谐振时对任一相电压数据进行非线性动力学分析，均能对其类型作出准确判断。

5)本文的研究为铁磁谐振类型的在线自动识别和谐振过电压的抑制策略研究奠定了一定的基础，为实测铁磁谐振数据的识别研究提供了新思路，丰富了铁磁谐振的研究实例。

参考文献

[1]Emin Z，Al Zahawi B A T，Auckland D W，et al.Ferroresonance in electromagnetic voltage transformers：a study based on nonlinear dynamics[J].IEE Proceedings-Generation，Transmission and Distribution，1997，144(4)：383-387.

[2]Mork B A，Stuehm D L.Application of nonlinear dynamics and chaos to ferroresonance in distribution systems[J].IEEE Transactions on Power Delivery，1994，9(2)：1009-1017.

[3]周丽霞，尹忠东，郑立.配网PT铁磁谐振机理与抑制的试验研究[J].电工技术学报，2007，22(5)：153-158.

Zhou Lixia，Yin Zhongdong，Zheng Li.Research on principle of PT resonance in distribution power system and its suppression[J].Transactions of China Electrotechnical Society，2007，22(5)：153-158.

[4]张博，鲁铁成，杜晓磊.中性点接地系统铁磁谐振非线性动力学分析[J].高电压技术，2007，33(1)：31-35.

Zhang Bo，Lu Tiecheng，Du Xiaolei.Nonlinear dynamic analysis of ferroresonance in neutral-grounded power system[J].High Voltage Engineering，2007，33(1)：31-35.

[5]Val E M，Dudurych I，Redfern M A.Characterization of ferroresonant modes in HV substation with CB grading capacitors[J].Electric Power Systems Research，2007，77(11)：1506-1513.

[6]Araujo A E A，Soudack A C，Marti J R.Ferroresonance in power systems：chaotic behaviour[J].Generation，Transmission and Distribution，IEE Proceedings C，1993，140(3)：237-240.

[7]Emin Z，Al Zahawi B A T，Yu K T，et al.Quantification of the chaotic behavior of ferroresonant voltage transformer circuits[J].Circuits and Systems I：Fundamental IEEE Transactions on Theory and Applications，2001，48(6)：757-760.

[8]Mozaffari S，Henschel S，Soudack A C.Chaotic ferroresonance in power transformers[J].IEE Proceedings-Generation，Transmission and Distribution，1995，142(3)：247-250.

[9]Kieny C.Application of the bifurcation theory in studying and understanding the global behavior of a ferroresonant electric power circuit[J].IEEE Transactions on Power Delivery，1991，6(2)：866-872.

[10]司马文霞，郑哲人，杨庆，等.用参数不匹配混沌系统的脉冲同步方法抑制铁磁谐振过电压[J].电工技术学报，2012，27(6)：218-225.

Sima Wenxia，Zheng Zheren，Yang Qing，et al.Suppressing the ferroresonance overvoltage by impulsive synchronization of chaotic systems with parameter mismatched[J].Transactions of China Electrotechnical Society，2012，27(6)：218-225.

[11]Takens F.Detecting strange attractors in turbulence[M]//Lecture Notes in Mathematica.Berlin：Springer Press，1981：366-381.

[12]Packard N H，Crutchfield J P，Farmer J D，et al.Geometry from a time series[J].Physical Review Letters，1980，45：712-715.

[13]行鸿彦，龚平，徐伟.嵌入窗方法确定混沌系统重构参数的仿真研究[J].系统仿真学报，2013，25(6)：1219-1225.

Xing Hongyan，Gong Ping，Xu Wei.Simulation research of chaos system reconstruction parameters based on embedded window[J].Journal of System Simulation，2013，25(6)：1219-1225.

[14]Albano A M，Muench J，Schwartz C，et al.Singular-value decomposition and the Grassberger-Procaccia algorithm[J].Physical Review A，1988，38(6)：3017-3026.

[15]Fraser A M，Swinney H L.Independent coordinates for strange attractors from mutual information[J].Physical Review A，1986，33(2)：1134-1440.

[16]Grassberger P，Procaccia I.Measuring the strangeness of strange attractors[J].Physica D Nonlinear Phenomena，1983，9(1/2)：189-208.

[17]Broomhead D S，King G P.Extracting qualitative dynamics from experimental data[J].Physica D，1986，20(2/3)：217-236.

[18]Kennel M B，Brown R，Abarbanel H D I.Determining embedding dimension for phase-space reconstruction using a geometrical construction[J].Physical Review A，1992，45(6)：3403-3411.

[19]Cao L Y.Practical method for determining the minimum embedding dimension of a scalar time series[J].Physica D，1997，110(1/2)：43-50.

[20]Kugiumtzis D.State space reconstruction parameters in the analysis of chaotic time series—the role of the time window length[J].Physica D：Nonlinear Phenomena，1996，95(1)：13-28.

[21]Kim H S，Eykholt R，Salas J D.Nonlinear dynamics，delay times，and embedding windows[J].Physica D：Nonlinear Phenomena，1999，127(1/2)：48-60.

[22]Otani M，Jones A.Automated embedding and creep phenomenon in chaotic time series[EB/OL].http：//users.cs.cf.ac.uk/Antonia.J.Jones/UnpublishedPapers/Creep.pdf/，2000-10-14/2011-03-15.

[23]Franca L，Savi M A.Distinguishing periodic and chaotic time series obtained from an experimental nonlinear pendulum[J].Nonlinear Dynamics，2001，26(3)：253-271.

[24]刘秉正，彭建华.非线性动力学[M].北京：高等教育出版社，2005.

[25]Grassberge P，Procaccia I.Characterization of strange attractors[J].Physical Review Letters，1983，50(5)：346-349.

[26]Kantz H，Schreiber T.Nonlinear time series analysis[M].Cambridge：Cambridge University Press，1997.

[27]张雨.时间序列的混沌和符号分析及实践[M].长沙：国防科技大学出版社，2007.

[28]Theiler J.Efficient algorithm for estimating the correlation dimension from a set of discrete points[J].Physical Review A，1987，36(9)：4456-4462.

[29]Grassberger P.An Optimized box-assisted algorithm for fractal dimensions[J].Physics Letters A，1990，148(1/2)：63-68.

[30]Schreiber T.Efficient neighbor searching in nonlinear time-series analysis[J].International Journal of Bifurcation and Chaos，1995，5(2)：349-358.

[31]杜林，李欣，司马文霞，等.110 kV变电站过电压在线监测系统及其波形分析[J].高电压技术，2012，38(3)：535-543.

Du Lin，Li Xin，Sima Wenxia，et al.Overvoltage on-line monitoring system for 110 kV substation and its waveforms analysis[J].High Voltage Engineering，2012，38(3)：535-543.

黄艳玲女，1978年生，博士，讲师，研究方向为电力系统过电压。

E-mail：huangyanling@cqu.edu.cn(通信作者)

司马文霞女，1965年生，教授，博士生导师，研究方向为电力系统的防雷与过电压防护、特殊环境中外绝缘放电特性及机理。

E-mail：cqsmwx@cqu.edu.cn

作者简介

中图分类号：TM864

收稿日期2015-03-04改稿日期2015-06-21

国家自然科学基金(51177182)、中央高校基本科研业务费(0209005206004)和国家创新研究群体科学基金(51321063)资助。