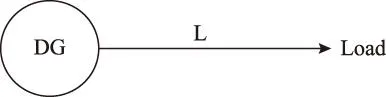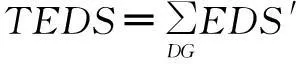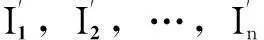重要区域孤岛微电网抗毁性规划初探
黄 帅 龙 燕 赵宏伟 冯 平 王虹淋
(1.后勤工程学院机械与电气工程系 重庆 401331
2.后勤工程学院军事供油工程系 重庆 401331)
重要区域孤岛微电网抗毁性规划初探
黄帅1,2龙燕1赵宏伟1冯平1王虹淋1
(1.后勤工程学院机械与电气工程系重庆401331
2.后勤工程学院军事供油工程系重庆401331)
摘要考虑到极端情况下重要区域配电网络的脆弱性,以逐渐成熟的微电网技术为基础,进行了以抗毁性为目标的微电网孤岛规划研究。首先,基于单个分布式发电(DG)对单个负荷供电的情况进行理论推导,建立了适用于微电网的抗毁性指标,并引入复杂网络理论优化了该指标的应用方法。以抗毁性指标最优为目标,对某重要区域孤岛微电网规划的实际问题建立了DG选址定容与网架规划交替迭代的联合规划模型,得到了随迭代次数变化的网络抗毁性指标及其对应的网架结构和DG分布情况。最后,以攻击策略为依据模拟了网络受打击情况,得到抗毁性评估结果。结果表明,抗毁性指标能较好的体现网络的抗毁性,而采用联合规划的方式能有效提升网络抗毁性。
关键词:微电网抗毁性孤岛规划复杂网络理论联合规划
Preliminary Study on Stand-Alone Microgrid Invulnerability Planning in Important Areas
HuangShuai1,2LongYan1ZhaoHongwei1FengPing1WangHonglin1
(1.Department of Machinery & Electrical EngineeringLogistical Engineering University Chongqing401331China 2.Department of Petroleum Supply EngineeringLogistical Engineering University Chongqing401331China)
AbstractConcerning the vulnerability of the important regional distribution network in extreme conditions,planning of the stand-alone microgird aiming at invulnerability is studied on the basis of a gradually mature microgrid technology.Firstly,an invulnerability index applied to the microgird is established through the theoretical derivation on the situation of a single distributed generation (DG) supplying a single load.Then the complex networks theory is introduced to optimize the applications of index.To solve an actual problem of the stand-alone microgrid planning in a certain important area,a joint planning model incorporating the DG locating and sizing model and the network planning model is established to optimize the suggested invulnerability index.With the varying number of iterations,the invulnerability indices and the corresponding grid structure and DG distribution are obtained.Finally,the invulnerability index is assessed in a simulated network attacking situation based on an attack strategy.The results show that the proposed index can clearly reflect the network invulnerability,and the joint planning method can effectively enhance the network invulnerability.
Keywords:Microgrid,invulnerability,stand-alone planning,complex network theory,joint planning
0引言
对于供电可靠性要求较高的中心城区、军事单位、重要机场和大型煤矿等区域,考虑到战争及袭击等极端情况,不同程度上存在过度依赖国家电网供电的问题,而集成利用分布式发电(Distributed Generation,DG)供电的微电网为区域供电的自给自足提供了技术基础[1]。然而,如何利用微电网技术增强战争及袭击等极端情况下区域供电的可靠性成为难题。随着与人类生活息息相关的网络(如因特网、交通网、电力网等)的高速发展,这些网络事故频发的现象引发了网络抗毁性的研究。复杂网络抗毁性理论针对较复杂的网络结构,分析事故隐患对整个网络的影响,并衡量网络系统在随机或蓄意破坏的情况下能否正常工作。随着研究不断深入,该理论在解决大型网络(如全球通信网络、全国物流网络等)抗毁性问题上得到一定应用[2-7]。但微电网规模较小且结构及运行原理难以用普通网络的边、节点关系描述,难以直接引入该理论。
目前,微电网或小型电网的抗毁性研究程度有限,虽然引入了复杂网络抗毁性理论的思想,但并未提出考虑电力网络独特性的微电网抗毁性指标,同时存在蓄意攻击手段有限和缺乏针对电网抗毁性的有效验证方式等问题[8-10]。文献[8]将复杂网络抗毁性理论的自然连通度指标和pajek网络抗毁性分析软件应用于中压配电网,分析了辐射网、环网、N供一备网、多分段多联络网抗毁性及网络中的薄弱节点,但在抗毁性分析中未考虑电力网络的特殊性,而将其作为普通网络进行研究。文献[9]将网络抗毁性指标中的等效最短路径数引入配电网建立了抗毁性测度指标,该指标通过比较待评价网络与全连通网络的差异得到待评价网络抗毁性,但该指标无法体现待评价电力网络能否正常工作。文献[10]引入节点脆弱性指标衡量小型电网对于蓄意攻击最薄弱节点手段的抗毁性,然而实际攻击中不能仅考虑最薄弱点遭受攻击情况,还需要考虑多个重要节点、多条线路同时遭受攻击的情况。
本文以极端条件为背景,假定微电网的DG和线路根据其重要性等因素遭受不同程度攻击,引入复杂网络抗毁性的思想建立了评价孤岛微电网抵抗蓄意攻击能力的抗毁性指标,提出了以该抗毁性指标为目标的孤岛微电网规划方法,并利用模拟攻击方式对抗毁性指标和规划方法进行验证和评估。
1模型假设
本文的研究对象为重要区域的微电网规划,故对于其他因素包括负荷点本身的抗毁性不予考虑,并假定负荷不会被摧毁,与微电网的接点始终不变,且在供电量充足的情况下保持运转。
1.1微电网设施设定
为了真实反映极端情况下重要区域微电网设施防护及隐蔽情况,假定微电网达到以下要求:①供电线路为难以直接发现和打击的地下电缆;②DG均有较好的伪装或隐蔽,且噪声等级低,噪声检测装置和红外装置不能直接定位。基于这样的设施水平,极端情况下抗毁性的研究才具有较普遍的意义。
1.2攻击策略设定
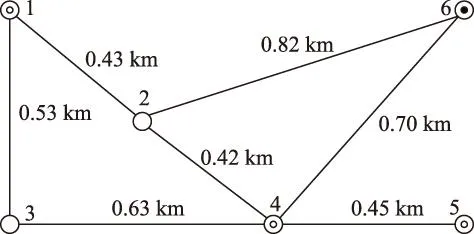
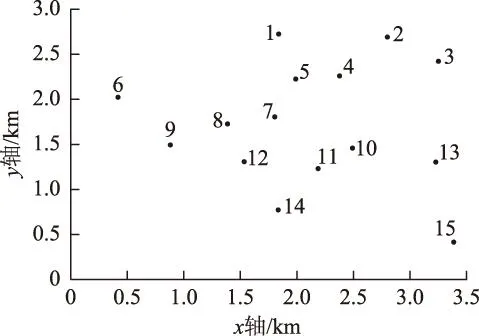
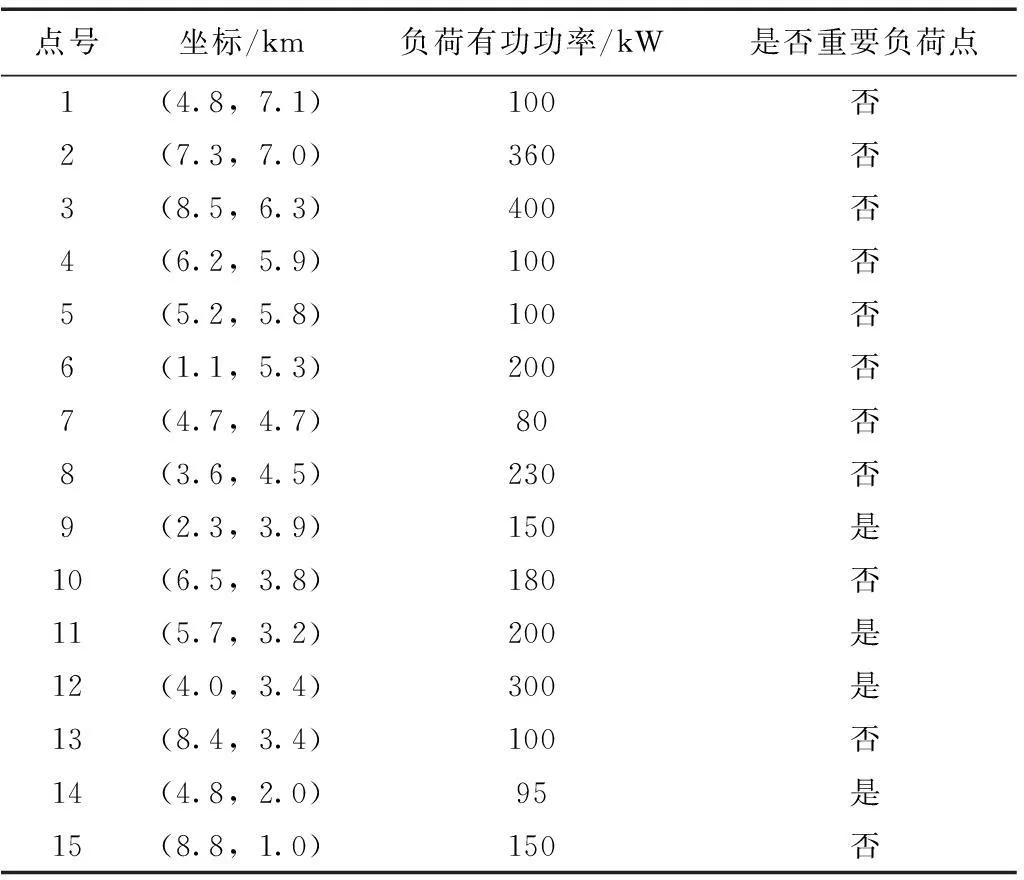
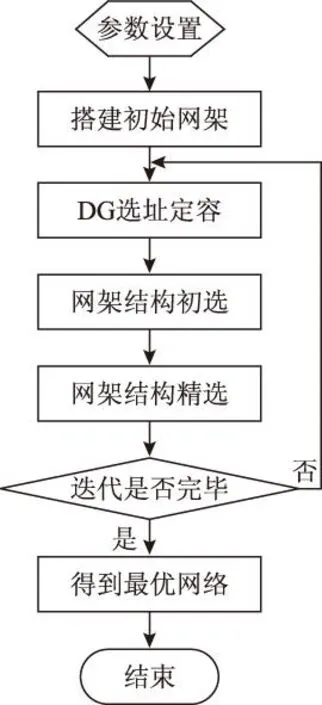
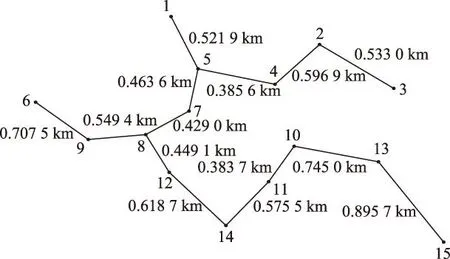
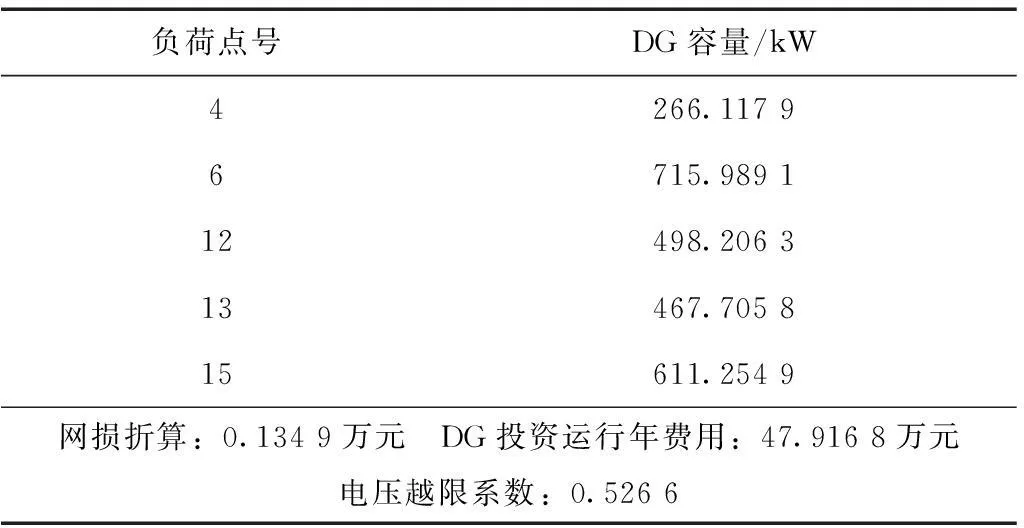
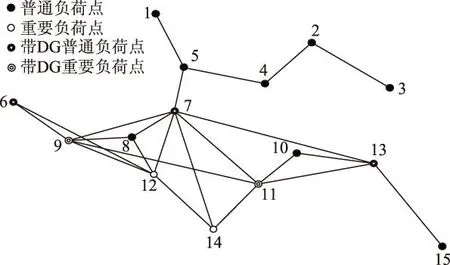
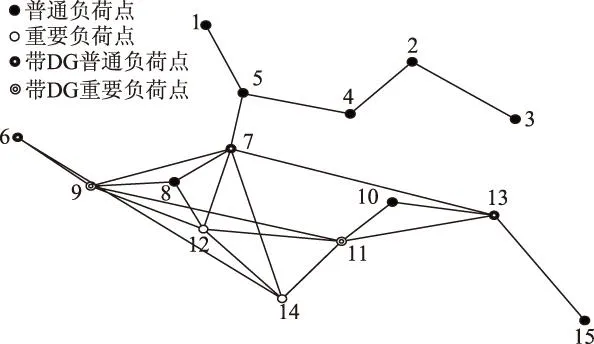
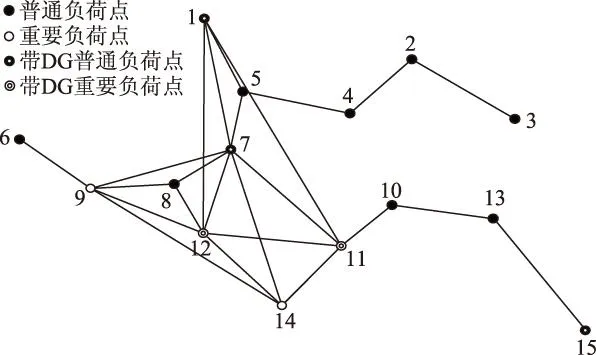
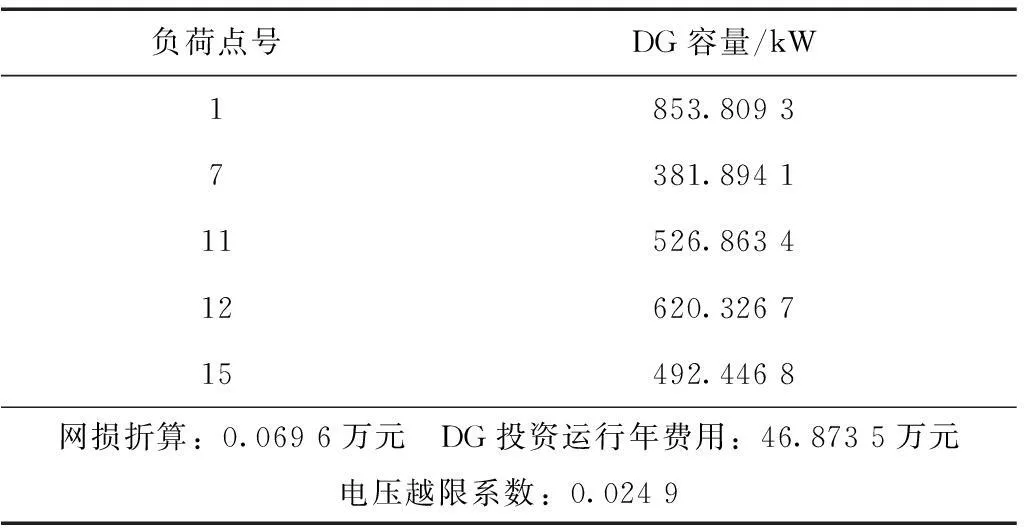
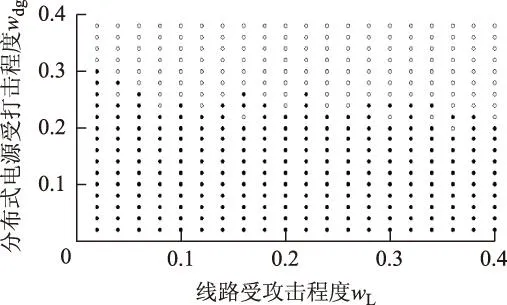
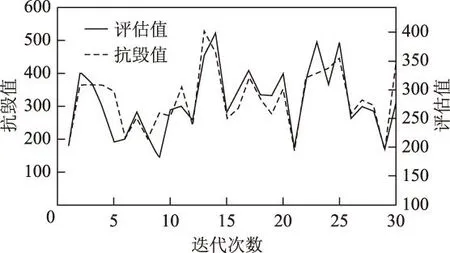
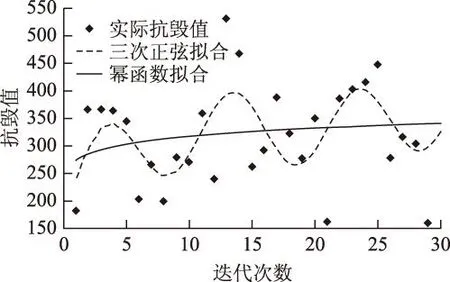
根据现代常规战争的经验,对重要区域电网设施的攻击以空中打击为主,包括轰炸、精确制导打击、石墨炸弹及电磁脉冲等方式。本文简化为以下攻击策略:①无目标设定的“地毯式”轰炸,随机损毁电缆,并暴露出隐藏的DG,攻击程度wL(0 2复杂网络抗毁性理论及其应用 2.1原理 (1) (2) S2越大,网络中替代线路冗余性越强,网络抗毁性越高。注意到计算中允许节点和边重复,闭途径可以为任意长度,导致S2→∞, 因此对nk加权,得到网络闭途径加权数S′[4,5] (3) 这样加权有以下原因:①闭途径边数越多,越易产生重复计算;②边数越多,对网络抗毁性贡献越小;③保证S′收敛[6]。经过吴俊等[7]的验证,S′可以体现出网络中替代路径的冗余性,进而表示网络的抗毁性。 2.2在微电网抗毁性中的应用 对于有冗余结构的微电网拓扑,从DG点到负荷点可能存在数条线路。 图1为某6节点微电网拓扑,图中带空心圈的节点1、节点4、节点5为带DG点,带实心圈的节点6为重要负荷点。在不考虑潮流的情况下,各DG供电给重要负荷的线路有:①节点1:126,1346,13426,1246;②节点4:46,426,43126;③节点5:546,5426,543126。 图1 某6节点微电网拓扑Fig.1 A 6 node network topology 如果不引入复杂网络抗毁性理论直接求取抗毁性指标,则存在以下问题: 1)线路所处网络位置不同对抗毁性指标的权重不同。例如,比较边26和边34,对负荷点6而言,边26处在中心位置,较为关键,而边34对网络抗毁性意义较低。在节点较多的网络中不同边和线路对网络抗毁性的贡献大小难以区分。 2)对每条线路的精确刻画使得线路搜索量和计算量很大,尤其在线路较多的网络中计算量难以估计。 故考虑将复杂网络抗毁性理论引入微电网,但微电网和复杂网络存在差异:①DG和负荷在微电网中的角色关系不能用复杂网络中的节点权值表达,负荷分级的概念在复杂网络理论中难以充分体现[8-10];②复杂网络抗毁性通常只计及边数对抗毁性影响,而未考虑线路实际长度影响,如节点1线路1346与节点5线路5426在复杂网络抗毁性分析中边数相同,而实际长度分别为1.86 km和1.69 km,存在较大差异,根据设定的攻击策略,线路实际长度不同对微电网抗毁性影响也不同;③微电网的规划对象相对于复杂网络来说节点数较少、拓扑结构简单,有条件对其进行精确刻画。故不能将复杂网络抗毁性理论直接引入微电网抗毁性分析。将复杂网络理论引入微电网抗毁性规划方法如下:将经过每个重要负荷点的网络分为闭途径、含闭途径的辐射网及辐射网3种类型,在抗毁性的度量上予以不同权重。 对于图1的微电网拓扑,根据该方法,将与负荷点6有关的线路列举出来:6246,621346,643124,621342,645,621345,6245。 线路数从原来的10条减少到7条。其中前两条线路为闭途径,第3、4条为含闭途径的辐射网,在计算抗毁性时给予较大权重,其余线路为辐射网,权重较小。运用复杂网络理论的相关知识,既区分了线路对抗毁性指标的影响等级,又减少了线路搜索计算量。 3微电网抗毁性指标 如图2所示,某DG通过线路L供电给负荷Load。设DG容量为Sdg,线路L长度为l, 负荷Load大小为SLoad。该线路所处网络中最大DG容量为Smax, 最长线路长度为lmax。 在第一种攻击策略中,对线路的攻击是随机的,故随着线路长度l的增加和攻击程度wL的增大,线路损毁概率PL也相应增大。假定PL对l服从均匀分布,在规划和评估中可认为PL与l和wL呈简单的正比关系。 (4) 图2 单DG对单负荷供电线路Fig.2 A single DG supply a single load 在第二种攻击策略下,对于第一种攻击策略后暴露的DG,优先摧毁容量大的DG,故DG损毁概率Pdg随DG自身容量Sdg和打击程度wdg的增大而增加。假定Pdg对Sdg服从均匀分布,在规划和评估中可认为Pdg与Sdg和wdg呈简单的正比关系。 (5) 由式(1)和式(2)得到该线路中单个DG对单个负荷的供电期望(Expected Demand Supplied,EDS)为 EDS=(1-PL)(1-Pdg)Sdg (6) 在式(6)中引入2.2节中的应用方法,首先搜索通过该单个负荷的所有线路,并区分这些线路的类型,将这些线路分为闭途径、含闭途径的辐射网和辐射网,再判断各DG所处的线路类型,最后根据线路类型给予各DG不同的权重,得到经过加权的单个DG对单个负荷的供电期望EDS′为 EDS′=kiEDS (7) 式中,ki(i=1,2,3)为DG处于不同种类线路时的加权值。本文中设定k1为DG处于闭途径的加权值;k2为DG处于含闭途径的辐射网的加权值;k3为DG处于辐射网的加权值。根据研究对象的不同,k1、k2、k3之间比重需要调整,但应遵循k1>k2>k3。 则所处网络中所有DG对单个负荷的供电期望(Total Expected Demand Supplied,TEDS)为 (8) 对单个负荷i的供电网络抗毁性Ii(Invulnerability)而言,在DG防护措施等条件相同的情况下,负荷i的SLoad越大,所需要的供电量也越大,抗毁性相应减弱。而总的供电期望TEDS越大,抗毁性越强。可以得出,Ii与SLoad呈反比关系,Ii与TEDS呈正比关系。 (9) 对于整个网络,需要让若干个重要负荷点同时保持持续供电状态。重要负荷点编号1到n,则整个网络的抗毁性指标I为各重要负荷点抗毁性中的最小值 I=min{I1,I2,…,In} (10) 在网架规划中,将以I为规划模型的目标,I越大的网架规划,抗毁性越强。 4某区域微电网抗毁性规划模型及求解 4.1问题分析 某重要区域负荷分布图如图3所示。 图3 重要区域负荷分布图Fig.3 Load distribution condition in an important area 图3中各负荷点的坐标、负荷有功功率及是否重要负荷情况如表1所示。 考虑到区域负荷分布情况及区域大小,准备进行电压等级10 kV的微电网规划。在平时,该电网能保证所有负荷点的正常供电;在极端情况下,应尽量保障重要负荷点9、11、12、14的供电充足,其中任意一点供电不足则视为网络失效。计算时的技术经济参数为:负荷功率因数均为cosφ=0.85, 电压降允许值±7%。 表1 重要区域负荷分布情况 为适应极端条件,结合该区域特点,DG采用低噪声的柴油机或微燃机较为合适。考虑到微燃机价格昂贵,目前应用并不广泛,规划中均按有关规范[11]采用同品牌低噪声可移动式100~1 000 kW柴油机组,设定最大安装数为5个。 4.2规划模型及求解 本规划问题为网架与DG的联合规划问题,目标是抗毁性指标I最优,约束是投资运行总费用。由于网络抗毁性能主要受网架结构直接影响,而网架的规划离不开DG的容量和位置信息,故整体规划采取网架规划与DG选址定容交替迭代进行的形式,通过一定的迭代次数找到最优的规划方案。总流程图如图4所示,迭代次数设置为30。投资运行总费用折算到年为C, 设线路投资维护年费用为C1, DG投资运行年费用为C2, 其关系为 C=C1+C2 (11) C1越大,在单位线路费用相同的情况下,可建设的线路越长,网架结构的冗余性越强,结构类似的情况下抗毁性指标I随之提高。C为约束值,C2越小,C1越大,故在DG选址定容模型中以C2最小为权重较大的目标。本次规划中设定C为100万元。 4.2.1初始网架搭建 采用最小生成树算法[12,13]得到总线路长度最短的初始网架如图5所示,该网架为辐射式结构。 4.2.2DG选址定容 DG选址定容问题为多目标优化问题,目标是使DG的投资运行年费用、网络损耗及电压稳定度达到总体最优。本文采用改进的粒子群算法[14-16]对其进行求解,得到DG分布情况、容量大小及各子目标值。对初始网络求解结果如表2所示。 图4 规划总流程图Fig.4 Flow chart of the total planning 图5 初始网架结构Fig.5 The initial grid structure 负荷点号DG容量/kW4266.11796715.989112498.206313467.705815611.2549网损折算:0.1349万元 DG投资运行年费用:47.9168万元电压越限系数:0.5266 DG投资运行年费用C2是该模型的权重较大的子目标。C2越小,总投资相同情况下用于网架规划的费用越多,从而间接提高了网络抗毁性。 4.2.3基于抗毁性指标的网架规划 总投资运行年费用C减去DG投资运行年费用C2为网架建设维护年费用C1。 考虑到模型假设中的微电网设施水平,网架均采用YJLV22-35型电缆,设定投资维护年费用为3万元/km[17]。 网架抗毁性规划问题是在一定成本约束下使网络抗毁性指标I最优的问题。指标I由式(1)~式(10)得到,式(7)中设k1=3, k2=1, k3=0.5。 先在成本约束C1下多次随机生成网架结构。以第17次迭代过程为例,该次迭代生成的随机网架中I最优的网络如图6所示,对应I=341.741 3, 该过程为初选,得到的网络为初选网络。 图6 第17次迭代初选网架结构Fig.6 Primary network structure in the 17th iteration 以初选出的网架结构为基础,采用禁忌搜索算法去边增边,得到新生成的网络中I最优的网架。具体算法策略为:①随机去掉现有的一条边s1成为网络net1,再随机选择除net1和s1以外的可能边s2添入net1成为新网络net2。若net2成本不过限,则再添进除net2及s1以外的s3,若过限,则重新选择s2,直至net2成本不过限,或不继续增加边,停止本次操作;②以上次操作得到的新网络为基础,重复①的操作,直至达到设定搜索量。该过程为精选,第17次迭代中的精选网络如图7所示,对应I=387.206 7。这次迭代中,精选后的网络与初选网络相比,更改边占初选网络边数的13.043 4%,抗毁性指标I提升了13.304 0%。加入精选环节能有效减少初选环节需要生成随机网络的个数,进而提高寻找某次迭代中精选网络的效率。 图7 第17次迭代精选网架结构Fig.7 Selected network structure in the 17th iteration 单次迭代过程得到的I最优网络即为精选网络,包括其对应的精选网架结构及DG选址定容情况。本次迭代得到的精选网络将用于求解下次迭代中DG选址定容情况,以该DG选址定容情况为基础进行本节中的操作将得到下次迭代中的精选网络。重复上述过程直至达到规定的迭代次数,得到所有迭代对应的精选网络。 4.2.4得到最优网络 迭代完毕后,从所有精选网络中筛选出I最优的网络为最优网络。本次规划得到的最优网络如图8所示,该网络对应的迭代次数为13,对应I=527.727 7,DG选址定容情况见表3。 图8 30次迭代中的最优网络Fig.8 The optimal network of 30 iterations 负荷点号DG容量/kW1853.80937381.894111526.863412620.326715492.4468网损折算:0.0696万元 DG投资运行年费用:46.8735万元电压越限系数:0.0249 5抗毁性评估 Edg=PdgSdg (12) (13) 式中,x为[0,1.1]上均匀分布的随机变量;PLi为第i条线路对应的损毁概率;Di为第i条线路是否被损毁,1表示未损毁,0表示损毁。值得注意的是,由于PLi取值范围为(0,1],为了避免PLi=1时第i条线路损毁概率为100%,x的分布范围不设为[0,1]而设为[0,1.1]。 (14) 图9为对第26次迭代产生的精选网络进行抗毁性评估的某次抽样结果,实心点表示网络在对应的wL和wdg下仍能有效工作,空心点表示对应情况下网络失效。图9中网络工作有效点总数为243,即该网络在总数为400中的243种模拟攻击方式下仍能维持全部重要负荷点正常工作。对该精选网络的全部抗毁性评估抽样结果进行平均得到最终的抗毁性评估值I′=248。 图9 某精选网络的抗毁性评估的某次抽样结果Fig.9 A sampling result of the invulnerability assessment of a selected network 得到所有迭代次数的精选网络的抗毁性评估值I′后,绘制I′与I随迭代次数的变化曲线,并在图10中对比。从图10可看出,I′在总体上能较好地反映I的大小及变化情况,两个指标的相关系数达到0.820 2,可认为I与I′有较强的相关性,验证了抗毁性指标I的有效性。但迭代次数为5、9、23等值时I与I′仍存在一定差异,产生差异的原因主要有:①评估过程中线路的损毁存在一定的随机性,虽然通过蒙特卡罗法减少了随机性的影响,但仍难以避免某些迭代点处的评估不受干扰;②抗毁性指标I为一系列函数计算得到的数值,而评估指标I′为有效点的数量,两者在度量上存在一定差异,难以做到完美的契合;③抗毁性指标I本身仍有不足,如式(9)中,本文认为Ii与SLoad呈简单的反比关系,可能造成指标本身不准确。 图10 I和I′随迭代次数变化情况Fig.10 I and I′ changing with the number of iterations 为了得到抗毁性指标I随迭代次数变化的规律,分别用三次正弦拟合法和幂函数拟合法对抗毁性指标I随迭代次数的变化情况进行拟合,如图11所示。 图11 抗毁性指标I的拟合Fig.11 The fitting of the invulnerability value I 从图11可看出,I的幅值随迭代次数的增加不断波动,总体呈上升趋势,证明DG选址定容和网架规划交替迭代的联合规划方式对抗毁性的提升有效。本次规划所有迭代中的最优网络对应迭代次数13,就是在迭代进行到43.3%时取得的,也验证了该规划方法寻优的有效性。 6结论 以战争及袭击等极端条件为背景,考虑电网受主动攻击情况,结合复杂网络抗毁性理论的思想,本文创建了适于衡量孤岛微电网抗毁性的指标I, 同时提出了以该指标为目标的DG选址定容和网架规划交替迭代的联合规划方式。该指标充分考虑了对电网的常规攻击策略和微电网结构及工作方式的特殊性,使指标较好地体现了微电网抗毁性的特点,同时采用区分DG所处线路类型并给予不同权重的方法减少了线路搜索量、提高了搜索效率,较好地区分了DG处于不同线路对抗毁性指标I的影响,从而优化了指标。网架规划中采用初选和精选结合的方式有效减少了初始随机网络数,提高了搜索精选网络的效率。以对电网的模拟攻击方式为基础,采用蒙特卡罗法建立了抗毁性评估模型,该评估模型验证了抗毁性指标I和联合规划方式的有效性和合理性。 参考文献 [1]黄帅,龙燕,冯平,等.微电源孤岛规划概述[J].电网与清洁能源,2014,30(5):7-12. Huang Shuai,Long Yan,Feng Ping,et al.An overview of stand-alone micro-sources planning[J].Power System and Clean Energy,2014,30(5):7-12. [2]Wu Jun,Tan Yuejin,Deng Hongzhong,et al.Relationship between degree-rank function and degree distribution of protein-protein interaction networks[J].Computational Biology and Chemistry,2008,32(1):1-4. [3]Li Jun,Wu Jun,Li Yong,et al.Attack robustness of scale-free networks based on grey information[J].Chinese Physics Letters,2011,28(5):1-4. [4]Li Yong,Wu Jun,Zou Anquan,et al.Effect of eliminating edges on robustness of scale-free networks under intentional attack[J].Chinese Physics Letters,2010.27(6):1-3. [5]田田,吴俊,谭跃进.基于自然连通度的复杂网络抗毁性仿真优化研究[J].复杂系统与复杂性科学,2013,10(2):88-93. Tian Tian,Wu Jun,Tan Yuejin.Simulation optimization for invulnerability of complex networks based on natural connectivity[J].Complex Systems and Complexity Science,2013,10(2):88-93. [6]Wu Jun,Mauricio B,Tan Yuejin,et al.Robustness of regular ring lattices based on natural connectivity[J].International Journal of Systems Science,2011,42(7):1085-1092. [7]Wu Jun,Mauricio Barahona,Tan yuejin,et al.Robustness of random graphs based on graph spectra[J].Chaos,2012,22(4):517-525. [8]曾新梅.中压配电网络拓扑结构抗毁性分析方法的研究[D].郑州:郑州大学,2012. [9]李珂,王金凤,杨丽徙,等.基于多场景抗毁性分析的配电网网络结构优化[J].电力系统自动化,2014,38(1):34-37. Li Ke,Wang Jinfeng,Yang Lixi,et al.Optimization of medium voltage distribution network based on multi-scenario survivability analysis[J].Automation of Electric Power Systems,2014,38(1):34-37. [10]李艳卿,李华强,李迁,等.基于节点脆弱性的电力系统抗毁性分析[J].四川电力技术,2014,37(1):26-28. Li Yanqing,Li Huaqiang,Li Qian,et al.The analysis of power system survivability based on node vulnerability[J].Sichuan Electric Power Technology,2014,37(1):26-28. [11]机械工业部标准化研究所.GJB 235A-1997军用交流移动电站通用规范[S].北京:国防科学技术工业委员会,1997. [12]刘健,杨文宇,余健明,等.一种基于改进最小生成树算法的配电网架优化规划[J].中国电机工程学报,2004,24(10):103-108. Liu Jian,Yang Wenyu,Yu Jianming,et al.An improved minmum-cost spanning tree based optimal planning of distribution networks[J].Proceedings of the CSEE,2004,24(10):103-108. [13]刘健,杨文宇,余健明,等.基于改进最小生成树算法并考虑负荷不确定性的配电网架最优规划[J].电网技术,2005,29(16):61-65. Liu Jian,Yang Wenyu,Yu Jianming,et al.Optimal distribution network planning based on improved minimal cost spanning tree algorithm and considering indeterminacy of power loads[J].Power System Technology,2005,29(16):61-65. [14]黄帅,龙燕,易斌,等.基于改进粒子群优化算法的微电网孤岛选址定容[J].后勤工程学院学报,2015,31(2):79-83. Huang Shuai,Long Yan,Yi Bin,et al.Stand-alone microgrid locating and sizing based on improved particle swarm optimization algorithm[J].Journal of Logistical Engineering University,2015,31(2):79-83. [15]李亮,唐巍,白牧可,等.考虑时序特性的多目标分布式电源选址定容规划[J].电力系统自动化,2012,36(5):1-6. Li Liang,Tang Wei,Bai Muke,et al.The multi-objective locating and sizing planning considering timing characteristics[J].Automation of Electric Power Systems,2012,36(5):1-6. [16]夏季,华志刚,彭鹏,等.基于非支配排序遗传算法的无约束多目标优化配煤模型[J].中国电机工程学报,2011,31(2):85-90. Xia Ji,Hua Zhigang,Peng Peng,et al.A model of unconstrained multi-objective optimization of coal blending based on the non-dominated sorting genetic algorithm[J].Proceedings of the CSEE,2011,31(2):85-90. [17]高笑.军事场所电能保障系统优化规划研究[D].重庆:后勤工程学院,2005. 黄帅男,1989年生,硕士,研究方向为微电网在军事领域的应用和军用电力系统运行与控制。 E-mail:542757469@qq.com 龙燕女,1964年生,教授,硕士生导师,研究方向为军用电力系统优化规划和营区智能化建设。 E-mail:longyanyan@163.com(通信作者) 作者简介 中图分类号:TM715 收稿日期2015-03-16改稿日期2015-06-05 重庆市自然科学基金资助项目(2006CK113)。