基于双矢量模型预测直接功率控制的双馈电机并网及发电
张 虎 张永昌 杨达维
(北方工业大学电力电子与电气传动北京市工程研究中心 北京 100144)
基于双矢量模型预测直接功率控制的双馈电机并网及发电
张虎张永昌杨达维
(北方工业大学电力电子与电气传动北京市工程研究中心北京100144)
摘要模型预测直接功率控制(MPDPC)以其原理简单、动态响应快和控制目标灵活等优点在并网变换器控制中得到了广泛关注。它利用系统模型来预测下一时刻的有功功率和无功功率,通过枚举比较得到使给定功率和反馈功率之间误差最小的电压矢量,相比传统的基于矢量表的直接功率控制具有更好的动态和稳态性能。为了进一步提高稳态性能并降低采样频率,提出一种基于双矢量的改进模型预测直接功率控制,即把一个控制周期分配给一个非零矢量和一个零矢量,通过优化非零矢量的作用时间来进一步减小功率脉动。通过合理安排矢量作用顺序甚至可以获得比传统MPDPC更低的开关频率而且稳态性能更好。在15 kW双馈风力发电系统上的仿真结果表明,相比传统MPDPC,所提出的双矢量MPDPC能够以更低的采样频率实现快速平滑的并网同步和灵活的有功、无功控制,并且开关频率更低,具有较大的实用价值。
关键词:双馈电机并网同步发电模型预测直接功率控制双矢量
Two-Vectors-Based Model Predictive Direct Power Control of Doubly Fed Induction Generator for Grid Connection and Power Regulation
ZhangHuZhangYongchangYangDawei
(Power Electronics and Motor Drive Engineering Research Center Beijing North China University of TechnologyBeijing100144China)
AbstractThe model predictive direct power control (MPDPC) is attracting wide attentions in the control of grid-connected converters due to the merits of simple principle,fast response,and flexible control aims.It uses the system model to predict the future value of active/reactive power and obtains the best voltage vector minimizing the power errors by enumeration.Compared to the conventional switching table based direct power control (DPC),MDPPC features better steady and dynamic performance.To further improve the steady state performance and reduce the sampling frequency,this paper proposes a two-vectors-based MPDPC by allocating one non-zero vector and one null vector during one control period.The power ripples are significantly reduced by optimizing the duration of the non-zero vector.Lower switching frequency with better steady state performance can be obtained by arranging the vector sequence in a more reasonable way.Simulation results from a 15 kW doubly fed induction generator (DFIG) system indicate that,compared to the conventional MPDPC,the proposed two-vectors-based MPDPC,with low sampling frequency,can achieve fast and smooth grid synchronization,flexible regulation of active/reactive power,and lower switching frequency.Hence,it is very practical for real applications.
Keywords:Doubly fed induction generator,grid synchronization,power generation,model predictive direct power control,two vectors
0引言
随着世界能源消耗的不断增长,新型可再生能源在过去几十年中飞速发展,而风能又在各种新能源中占主导地位。如今,风力发电已从早期的恒速恒频系统发展成为现在的变速恒频系统,具有更小的机械应力和能量波动,更高的风能捕获能力,更快速的动态响应以及更灵活的有功、无功控制方式。其中基于双馈电机(Doubly Fed Induction Gererator,DFIG)的风力发电系统由于其变换器的功率只有额定发电功率的25%~30%,是目前应用较为广泛的变速恒频风力发电系统[1]。
目前已经有多种控制策略应用于双馈电机的控制,其典型代表是矢量控制(Vector Control,VC)。它在定子磁链定向的同步旋转坐标系中把转子电流分解为转矩(有功)分量和磁链(无功)分量,然后用PI等线性控制器分别进行调节[2,3]。虽然矢量控制可以得到较好的稳态性能,但是它对参数的依赖性较强,而且需要相对繁复的控制器调试工作。
近年来,直接转矩控制(Direct Torque Control,DTC)[4,5]和直接功率控制(Direct Power Control,DPC)[6,7]被应用于双馈电机控制并得到了国内外学者的广泛关注。它们采用滞环比较器替代矢量控制中的PI调节器,根据转子磁链所在扇区从优化矢量表中选择能够减少反馈值和参考值之间误差的电压矢量。这种控制方式具有快速的动态响应且显著减少了调试工作,不足之处是开关频率随工作点而变化,稳态性能较差。导致DTC/DPC产生上述问题的原因是用于选择矢量的开关表只是一个启发式的矢量表,在某些区域选择的矢量是无效甚至错误的。为解决这个问题,人们又提出了一种更完整准确的方法,即模型预测控制(Model Pridictive Control,MPC)。在MPC中考虑了完整的电机和变换器模型[8,9],因此在选择矢量上更加精确有效,能够获得更好的控制效果。
传统MPC在一个控制周期中只发出一个电压矢量,为了取得较好的控制效果,需要较高的采样频率,而且开关频率依然是变化的。本文提出一种双矢量模型预测直接功率控制(Model Predictive Direct Power Control,MPDPC),通过引入矢量占空比的概念来减小功率脉动。首先按照使给定功率和反馈功率误差最小的原则得到最佳非零矢量,然后把一个控制周期分成两个时间段分别给非零矢量和零矢量,其中非零矢量的作用时间根据功率误差最小的原理计算得到。通过合理安排矢量作用顺序并考虑到前后控制周期间相邻矢量的衔接,可以进一步降低开关频率。本文提出的MPDPC不仅可用于并网发电,而且适用于并网同步过程,避免了传统矢量控制中对多个PI系数的整定。在Simulink环境中对一台15 kW双馈风力发电机系统进行了仿真,并和传统单矢量MPDPC进行了对比,结果验证了所提方法的可行性及在性能上的改进。
1双馈电机数学模型
双馈电机在转子坐标系中的数学模型可以用复矢量表示为[10,11]
(1)
(2)
ψs=Lsis+Lmir
(3)
ψr=Lmis+Lrir
(4)
(5)
式中,us、is、ur、ir、ψs和ψr分别为定子电压、定子电流、转子电压、转子电流、定子磁链和转子磁链;Rs、Rr、Ls、Lr和Lm分别为定子电阻、转子电阻、定子电感、转子电感和定转子间互感;ωr为转子的电角速度;p为极对数;λ=1/(LsLr-Lm2)为漏感系数。
根据式(3)和式(4),定子和转子电流可以用定子和转子磁链表示为
is=λ(Lrψs-Lmψr)
(6)
ir=λ(-Lmψs+Lsψr)
(7)
定子侧的复功率矢量S可以用定子侧电压和电流得到
(8)
或者在忽略定子电阻后用定子和转子磁链表示为[11]
(9)
式中,kσ=1.5λωg,ωg为电网角频率。
对式(9)进行分解,可以得到有功和无功功率为
(10)
(11)
联立式(1)、式(2)和式(6)~式(8)经过推导可得复功率S的导数为[11]
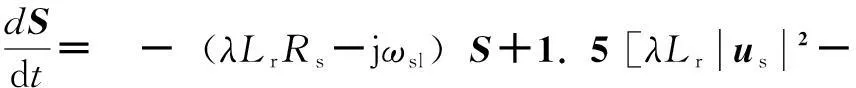
(12)
式中,ωsl=ωg-ωr是转差角速度。
对式(12)进行实部与虚部的分解可以得到有功功率和无功功率对时间的导数为dP/dt=Re(dS/dt),dQ/dt=Im(dS/dt)。
需要说明的是,式(12)虽然是在转子坐标下推导得到,但它在别的坐标系的形式并不发生变化。原因在于功率关系与具体坐标选取无关,只是需要把所有变量统一到相同坐标下表达即可。
2双馈电机并网原理
双馈电机在并入电网前is=0,此时双馈电机的数学模型由式(1)~式(4)得到
(13)
(14)
ψs=Lmir
(15)
ψr=Lrir
(16)
为实现平滑同步并网,定子侧的感应电压us应与电网电压ug在频率、相位和幅值上完全一致。这可以等效为它们的积分完全相等,即
(17)
式中,ψg为电网虚拟磁链。联立式(15)~式(17)可得最终满足并网的条件为
(18)
由式(14)和式(16)可知ψr与ur之间为一阶惯性关系。本文在并网前后均使用MPDPC的框架,为此定义一个虚拟复功率为[12]
(19)
与式(9)相比,虚拟复功率只是将式(9)中的ψs换成ψg,因此很容易实现并网前后在控制上的一致。把式(18)代入式(19),很容易得到同步并网的条件为Sv=0,也即虚拟有功和无功均为零。
对式(19)求导,可以得到Sv的导数为
(20)
对式(20)进行实部与虚部的分解,可以得到虚拟有功和虚拟无功的导数为dPv/dt=Re(dSv/dt),dQv/dt=Im(dSv/dt)。
并网和发电过程可概述如下。在并网前,复功率参考值为零,反馈值是虚拟复功率,目的在于使得定子侧感应电压与电网电压相同,实现快速平滑且无冲击的柔性并网。并网后灵活的有功无功调整是关键,尤其当电网需要进行无功补偿以支撑电网电压或改进电能质量时。当电机满足发电条件时,电机进入发电模式,有功和无功功率的参考值来自风速和电网负载的要求,反馈值从虚拟复功率切换为实际的复功率。
3基于MPDPC的双馈电机并网及发电
3.1MPDPC基本原理
传统的DPC通过检测有功、无功功率与给定值的误差及转子磁链的扇区位置,从事先定义的矢量表中选择出所需的转子电压矢量。而MPDPC通过在线计算每一个可能的转子电压矢量,选择出使实际值与给定值误差最小的一个矢量。由于使用了完整的电机模型,MPDPC在矢量选择上更加精确有效,具有更好的控制性能。其不足之处是采样频率较高而且稳态性能依然有待提高。本文在单矢量MPDPC的基础上,在每一个控制周期中同时施加一个非零矢量和一个零矢量,由于零矢量产生的有功和无功变化较小,二者相配合通过优化矢量时间可以在不影响动态性能的情况下减小功率脉动。
目标函数的建立是MPC的一个重要环节。鉴于研究对象是用于风力发电的DFIG,目标函数考虑有功和无功功率的误差最小,所以设目标函数为
(21)
式中,k+1表示下一时刻,Sk+1在并网前是虚拟复功率,由式(19)得到,在并网后则是实际复功率,由式(9)得到。
由式(1)~式(4)可知,双馈电机的模型可以表示为空间状态方程形式,即
(22)
(23)
式中,ψs和ψr为状态变量[13]。将式(22)和式(23)离散化,可以得到k+1时刻的ψs和ψr为
(24)
(25)
式中,Ts是控制周期。
对于三相对称正弦电网来说,有dug/dt=jωgug,忽略定子电阻压降有dψg/dt=ug,则k+1时刻的虚拟磁链ψg由电网电压得到
(26)
3.2矢量作用时间优化
当最佳的非零矢量被选出来后,则需要确定其作用时间。本文中,通过使式(21)最小化来确定非零矢量作用时间。设有功功率(或虚拟有功功率)的导数在非零矢量和零矢量作用时间分别是s1和s2,无功功率(或虚拟无功功率)的导数在非零矢量和零矢量作用时间分别是s11和s22。并网前,虚拟有功功率和虚拟无功功率的导数可由式(20)的实部和虚部得到;并网后,实际有功功率和实际无功功率的导数可由式(12)的实部和虚部得到。有功功率(或虚拟有功功率)和无功功率(或虚拟无功功率)在控制周期结束时可表示为
pk+1=pk+s1tv+s2(Ts-tv)
(27)
qk+1=qk+s11tv+s22(Ts-tv)
(28)
式中,tv是非零矢量的作用时间。
在一个控制周期中使得式(21)中的目标函数F最小的tv需要满足条件[14]
(29)
求解式(29)可以得到

(30)
需要注意的是,tv的解小于0时,tv的值应该限制为0;tv的解大于Ts时,tv的值应该限制为Ts。
3.3开关频率降低
在大功率风力发电系统中,为减少开关损耗,提高系统效率,降低开关频率尤为重要。本文通过合理安排矢量作用顺序,在不影响系统性能的情况下有效降低了开关频率。通常情况,先施加非零矢量,再施加使开关状态跳变最少的零矢量。例如,如果选择的最佳非零矢量为“110”,则零矢量应该选择“111”而非“000”。此外,还需要考虑相邻两个矢量序列之间的衔接问题。比如上一个周期的矢量序列为“100,000”,若下一个周期所选矢量为“001”和“000”,则为减小开关频率,应该先施加零矢量“000”。需要指出的是,如果矢量次序发生了变化,相应的矢量时间也要跟着调整。
3.4一拍延时补偿
众所周知,实际数字控制系统中存在一拍延时。变量xk在k时刻被采集,系统需要一小段时间来计算,当得到需要的电压矢量vkr时,实际上直到k+1时刻才会发出该电压矢量,但此时变量xk已经变化成了xk+1,因此由k时刻求得的vk作用在k+1时刻未必是最佳矢量,影响了控制效果。因此为消除一拍延时的影响,式(21)中Sk+1应该被替换成Sk+2,即目标函数应写为
(31)
得到Sk+2需要两步预测,其中k+1时刻的变量可以由式(24)~式(26)求出作为k+2时刻变量的初值,然后针对每个非零电压矢量来重复此预测过程,直到求得最佳的非零电压矢量,最后应用式(30)求解非零矢量的最优作用时间,只不过等号右边的变量需要向前推进一个时刻。
实际实现时单、双矢量MPDPC可以采用同一程序框架。首先是一拍延时补偿,然后是功率导数计算,借助功率导数单矢量MPDPC可以直接得到下一时刻的功率预测值,通过最小化目标函数得到最佳电压矢量。至此,单矢量MPDPC执行完毕,而双矢量MPDPC则需要进一步计算最优非零电压矢量的作用时间,如式(30)所示。这会使计算量相比单矢量MPDPC略有增加,但并不会对程序执行的实时性带来较大影响。
4仿真结果
为了验证双矢量MPDPC的有效性,在Matlab/Simulink环境下对一台15 kW的双馈发电机进行了仿真。电机参数见表1。作为对比,文中还给出了相同测试条件下传统单矢量MPDPC在10 kHz采样频率的结果。为了验证本文所提方法的优越性,双矢量MPDPC的采样频率是5 kHz。电机于0.05 s开始同步,0.2 s并网,0.3 s开始发电。
4.1同步及并网过程
图1为并网前的同步过程,电机转速为80%额定转速,虚拟复功率给定值为0,在0.05 s开始同步,图中从上至下曲线依次为虚拟无功、虚拟有功和转子电流。可以看出,两种方法都可以使虚拟有功和无功快速地跟踪到给定值,实现平滑的电网电压同步,但双矢量MPDPC功率脉动和转子谐波明显更小,表现出优异的稳态性能。

表1 电机参数
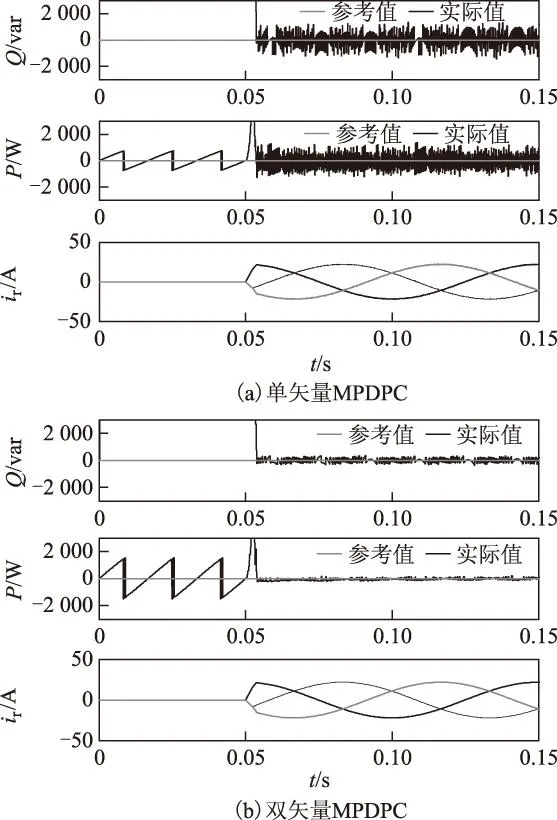
图1 并网前虚拟有功、无功功率和转子电流响应Fig.1 Response of virtual active power,reactive power and rotor current before grid connection using conventional MPDPC and two-vector-based MPDPC
图2为两种方法从同步到并网的过程,电机于0.2 s开始定子侧接入电网,但有功、无功功率给定值仍然为0,尚未开始发电,因此定子电流基本为零。图中从上至下的曲线依次为实际无功功率、有功功率、定子电流、转子电流和定子/电网电压。可以看出虽然同步后定子侧电压为PWM波,含有高次谐波,但与实际电网电压在基波频率、幅值和相位上完全一致,因此并网时没有任何冲击,实现了柔性并网,这从定子电流波动很小上可以得到验证。与单矢量MPDPC相比,双矢量MPDPC仍然在功率和电流上具有更小的脉动和谐波,稳态性能更好。
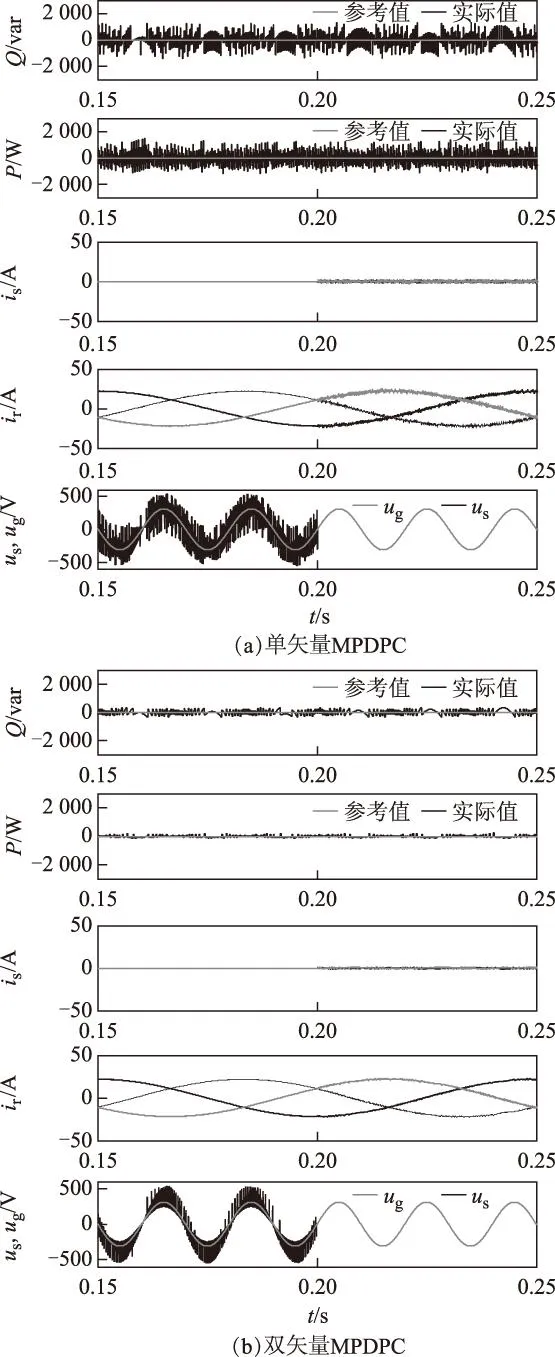
图2 并网过程有功、无功功率,转子电流和定子/电网电压响应Fig.2 Response of active power,reactive power,rotor current and stator/grid voltage during grid connection using conventional MPDPC and two-vector-based MPDPC
4.2并网发电过程
本文采用电动机惯例,因此发出功率时为负值。图3为转速固定为80%同步转速,有功和无功参考值发生阶跃时的实际无功功率、有功功率、定子电流、转子电流和非零矢量的占空比。无功给定值于0.4 s从0变为11 kvar,在0.6 s变为-11 kvar;有功给定在0.3 s从0变到-15 kW,在0.5 s变到-7.5 kW。可以看出双矢量MPDPC具有与传统单矢量MPDPC同样快速的动态响应,但在稳态性能上表现更佳,呈现出更小的功率脉动和电流谐波。非零矢量的占空比大部分条件下小于1,这表明要实现对功率的精确调节并不需要最佳电压矢量施加在整个控制周期,这也是传统单矢量MPDPC稳态性能差的主要原因。
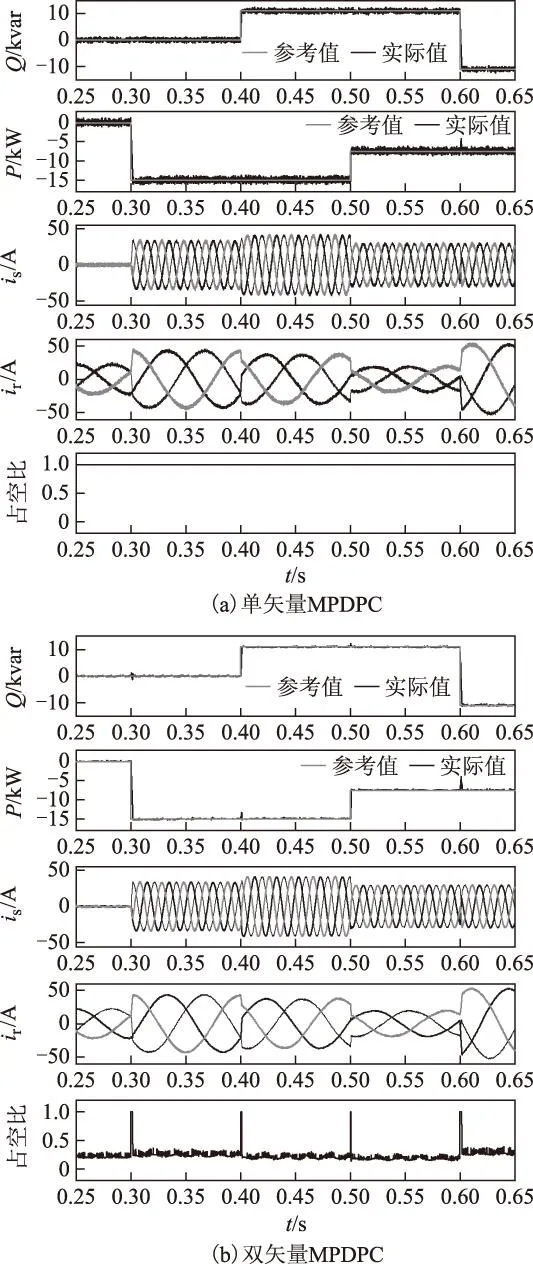
图3 功率阶跃变化,转速恒定条件下的响应结果Fig.3 Response to step changes in power references with fixed rotor speed using conventional MPDPC and two-vector-based MPDPC
图4进一步给出在转子转速变化时双馈发电机的无功功率、有功功率、定子电流、转子电流和占空比。转速在0.35~0.55 s内从80%同步转速线性变化到120%同步转速。可以看出采用本文提出的双矢量MPDPC在转速变化时仍可实现对给定功率的快速精确跟踪。
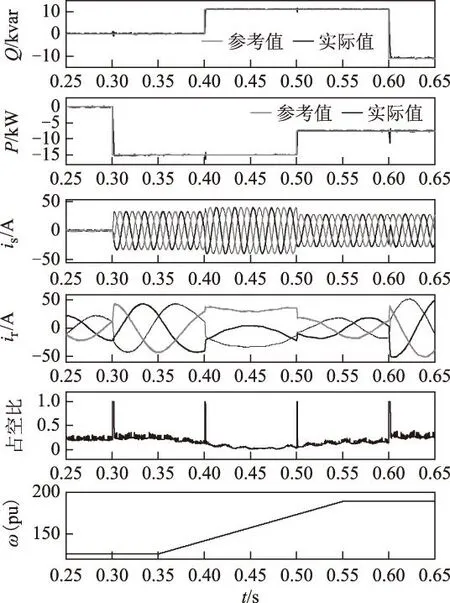
图4 双矢量MPDPC在功率阶跃变化,转速变化条件下的响应结果Fig.4 Response of the step change in reference power with variable rotor speed with two-vector MPDPC
双馈风力发电机经常需要运行在转子转速变化,功率给定变化的情况下。图5给出了转子转速从80%同步转速变化到120%同步转速,有功功率给定以频率5 Hz、幅值7.5 kW进行变化,而无功功率阶跃变化的情况下,双矢量MPDPC的控制效果。可以看出实际功率仍然很好地跟踪了给定功率。
4.3电流THD分析
为进一步对比两种控制方法的稳态性能,图6给出了转速为80%同步转速,有功功率为-15 kW,无功功率为11 kvar时,单矢量MPDPC和双矢量MPDPC的定转子电流的频谱分析。单矢量MPDPC的定转子电流具有较宽的频谱,定转子电流THD分别为2.09%和3.79%,而双矢量MPDPC的定转子电流THD分别为0.9%和1.91%,而且谐波主要集中在5 kHz的采样频率,方便了滤波器设计。
4.4开关频率比较
本文中单矢量MPDPC的采样频率为10 kHz,其平均开关频率为4.15 kHz。双矢量MPDPC的采样频率只有5 kHz,平均开关频率为2.13 kHz。可以说采用双矢量MPDPC后,可以用更低的采样频率获得更好的稳态性能,同时开关频率更低,因此更加实用。


图5 双矢量MPDPC在转子转速变化、有功给定正弦变化和无功给定阶跃变化时的响应Fig.5 Tracking behavior of the two-vector-based MPDPC with variable speed under the condition of sinusoidal active power reference and stepped reactive power reference
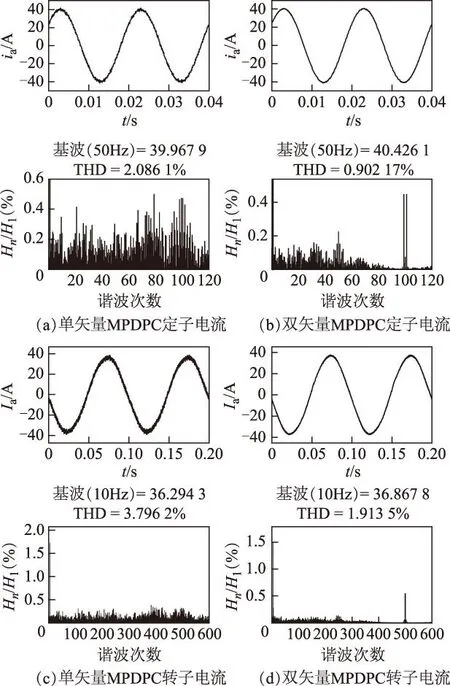
图6 定转子电流及其频谱Fig.6 Harmonic spectrum of stator/rotor current
为了进一步降低开关频率以适应大功率场合,这里对3.3节提出的减小开关频率的方法进行了验证,实验条件与发电阶段的图3b相同。图7为使用减小开关频率方法后的波形,与图3b相比变化不大。图8为使能和未使能开关频率降低策略后的平均开关频率的对比(0.3~0.6 s)。可以看到使能开关频率降低后,功率脉动有微小的增加,但开关频率由2.13 kHz下降到1.60 kHz,下降幅度达24.9%,验证了该方法对减小开关频率的效果。
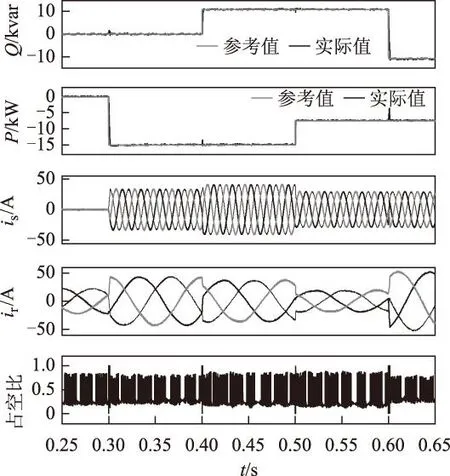
图7 使能开关频率降低的双矢量MPDPC在功率阶跃变化,转速恒定条件下的波形Fig.7 Response to step change in reference power with fixed rotor speed for two-vector-based MPDPC with switching frequency reduction
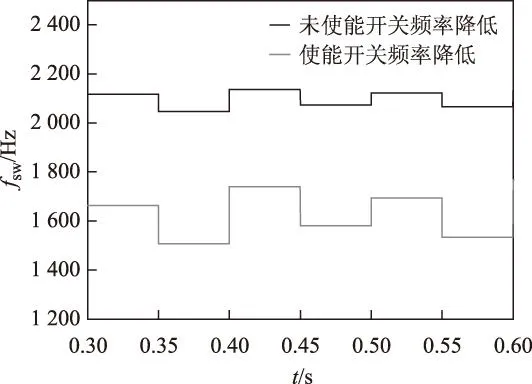
图8 双矢量MPDPC在使能和未使能开关频率降低策略时的平均开关频率比较Fig.8 Average switching frequency for two-vectors-based MPDPC with and without switching frequency reduction
5结论
本文针对双馈风力发电机控制系统提出了一种改进的双矢量模型预测直接功率控制。不同于传统MPDPC在一个控制周期内只采用单个矢量带来的采样频率高、稳态性能相对较差和开关频率高等问题,改进的双矢量MPDPC在每个控制周期使用一个非零矢量和一个零矢量的组合。首先针对所有非零电压矢量来预测下一时刻的有功和无功功率,通过枚举比较得到使下个周期内功率误差最小的最佳电压矢量,进一步按照有功和无功在控制周期结束时误差最小的原则来解析求得该最佳非零矢量的作用时间。相比传统单矢量MPDPC,本文提出的双矢量MPDPC具有更优越的稳态性能和同样快速的动态响应,同时具有更低的采样频率和开关频率。文中详细讨论了矢量选择、占空比计算、开关频率降低和一拍延时补偿等问题,并将该方法用到并网同步和并网发电等过程。通过一系列仿真和对比结果,可以看出双矢量MPDPC并网快速平滑,有功、无功功率灵活可调,相比单矢量MPDPC在更低开关频率下获得了更小的功率脉动和电流THD,验证了该方法的有效性和优越性。
参考文献
[1]Li H,Chen Z.Overview of different wind generator systems and their comparisons[J].IET Renewable Power Generation,2008,2(2):123-138.
[2]杨睿茜,陈红坤,陶玉波,等.双馈式风机控制器参数整定的实用方法[J].电力系统保护与控制,2015,43(2):63-69.
Yang Ruixi,Chen Hongkun,Tao Yubo,et al.A practical method on doubly-fed induction generator controller parameter determination[J].Power System Protection and Control,2015,43(2):63-69.
[3]严干贵,侯延鹏,王健,等.抑制超速脱网的双馈感应风电机组低电压穿越控制策略研究[J].电工技术学报,2015,30(23):146-154.
Yan Gangui,Hou Yanpeng,Wang Jian,et al.A DFIG wind turbine low-voltage ride-through control strategy restraining over-speed-tripping-off from grid[J].Transactions of China Electrotechnical Society,2015,30(23):146-154.
[4]Buja G S,Kazmierkowski M P.Direct torque control of PWM inverter-fed AC motors—a survey[J].IEEE Transaction on Industry Electronics,2004,51(4):744-757.
[5]Arnalte S,Burgos J C,Rodriguez Amenedo J L.Direct torque control of a doubly-fed induction generator for variable speed wind turbines[J].Electric Power Components and System,2002,30(2):199-216.
[6]孙丹,方扬,孙士涛,等.双馈异步风力发电机无差拍直接功率控制及延时补偿[J].电工技术学报,2013,28(11):70-77.
Sun Dan,Fang Yang,Sun Shitao,et al.Dead-beat direct power control of doubly fed induction generators with delay compensation[J].Transactions of China Electrotechnical Society,2013,28(11):70-77.
[7]Datta R,Ranganathan V T.Direct power control of grid-connected wound rotor induction machine without rotor position sensors[J].IEEE Transactions on Power Electronics,2001,16(3):390-399.
[8]Cortes P,Kazmierkowski M,Kennel R,et al.Predictive control in power electronics and drives[J].IEEE Transactions on Industry Electronics,2008,55(12):4312-4324.
[9]Zhang Y,Zhu J,Hu J.Model predictive direct torque control for grid synchronization of doubly fed induction generator[C]//Proceedings of IEEE Int.Electric Machines and Drives Conference,IEMDC ’11,Toront,Canada,2011:775-780.
[10]战亮宇,金新民,张禄.双馈电机复功率特性研究及四维分析[J].电工技术学报,2012,27(1):131-135.
Zhan Liangyu,Jin Xinmin,Zhang Lu.Complex power characteristics of doubly-fed induction machine and its four dimesion analysis[J].Transactions of China Electrotechnical Society,2012,27(1):131-135.
[11]Zhang Y,Hu J,Zhu J.Three-vectors-based predictive direct power control of the doubly fed induction generator for wind energy applications[J].IEEE Transactions on Power Electronics,2014,29(7):3485-3500.
[12]Zhang Y,Li Z,Xie W.Grid synchronization of DFIG using model predictive direct power control[C]//Electrical Machines and Systems(ICEMS),Beijing,2011.
[13]Zhang Y,Li Z.Predictive direct torque and flux control of doubly fed induction generator with switching frequency reduction for wind energy applications[C]//Electrical Machines and Systems (ICEMS),Beijing,2011.
[14]Zhang Y,Xie W,Li Z.Model predictive direct power control of a PWM rectifier with duty cycle optimization[J].IEEE Transactions on Power Electronics,2013,28(11):5343-5351.
张虎男,1976年生,博士,讲师,研究方向为交流电机控制。
E-mail:zh@ncut.edu.cn
张永昌男,1982年生,博士,研究员,研究方向为电力电子与电机控制。
E-mail:yongzhang@ieee.org(通信作者)
作者简介
中图分类号:TM614
收稿日期2014-09-24改稿日期2015-12-24
国家自然科学基金(51207003、51577003)和北京市科技新星计划(xx2013001)资助项目。

