基于ANSYS的高压大截面电缆金具短路电动力和机械应力分析

刘航宇　刘　念　蒲丽娟　游世良　吴　昊　李　娟

(1.四川大学电气信息学院　成都　610065

2.四川电力设计咨询有限公司　成都　610016)



基于ANSYS的高压大截面电缆金具短路电动力和机械应力分析

刘航宇1刘念1蒲丽娟1游世良2吴昊2李娟1

(1.四川大学电气信息学院成都610065

2.四川电力设计咨询有限公司成都610016)

摘要采用暂态短路电流计算方法和有限元法，分析了高压大截面电缆短路电动力的计算过程，推导出高压大截面电缆金具短路电动力的计算公式，同时考虑电缆蛇形敷设因素、导体外层介质缓冲作用及电缆位移偏转量，引入短路电动力工频分量(50 Hz)修正系数K1和两倍工频分量(100 Hz)修正系数K2对作用在电缆金具上的短路电动力进行修正。基于ANSYS建立电缆金具系统三维有限元计算模型，分别研究电缆敷设跨距和相间距对金具应力场的影响，并对双桥子-桃乡220 kV电缆段进行计算。由计算结果可知，在螺杆中点处产生的应力最大，即该位置最易变形或拉裂，对于220 kV电缆工程中“一”字形排列形式，电缆敷设跨距和相间距分别应满足l≤2.7 m，0.28 m≤a≤0.30 m。

关键词：大截面电缆金具短路电流电动力有限元计算

ANSYS Based Analysis on Short-Circuit Force and Mechanical Stress of Cleats for High Voltage Large Cross-Sectional Cables

LiuHangyu1LiuNian1PuLijuan1YouShiliang2WuHao2LiJuan1

(1.College of Electrical Engineering & Information TechnologySichuan University Chengdu610065China 2.Sichuan Electric Power Design & Consulting Co.LTDChengdu610016China)

AbstractBased on transient short-circuit current calculation methods and finite element method (FEM)，the calculation process of the short-circuit forces for high voltage large-sectional cables is analyzed.And the short-circuit forces calculation formula for cleats of high voltage large cross-sectional cable is gotten.Within the formula，the snake-like layout of the cable，the mediums cushion effect at the outer conductor，and the cable movement are taken into consideration.Moreover，the coefficientsK1andK2are introduced to modify the expression of the cable cleat force caused by 50 Hz and 100 Hz frequencies respectively.The 3D finite element calculation model of the cable cleat system is established based on ANSYS.Then the effect of span spacing and phase spacing on the cable cleats stress field has been studied.At the same time，the 220 kV power cable transmission line between Shuang Qiaozi and Tao Xiang has also been calculated.As can be seen from the simulation results，the maximum value of the stress is in the middle of the bolt.So it is most easy to deform or be pulled apart.The span and phase spacing should satisfy the standardl≤2.7 m，0.28 m≤a≤0.30 m separately for 220 kV power cable transmission lines which are laid in parallel.

Keywords：Large section cable，cleats，short-circuit current，electromagnetic force，FEM calculation

0引言

随着城市工业负荷的快速增长，城市建设与线路走廊的矛盾使得截面积大于2 000 mm2的电缆正越来越多地应用于城市用电负荷中心。国外对电压等级为20 kV及以下、且为三角形敷设的单芯电缆在短路时进行了研究。研究表明，电缆冲击电流最大值为105 kA，如此大的冲击电流将在三相导体间产生巨大的电动力，该电动力可能瞬间摧毁整条电缆线路。短路电动力将导致电缆内部结构发生位移，结构变化将导致电缆内部电场畸变而发生局部放电使得绝缘被击穿。研究对电缆金具安装最大跨距和中间捆绑带长度做出了规定[1-4]，但对110 kV及以上电压等级并未进行研究，同时并未提及金具参数优化问题。

电缆金具是安装在电缆线路上，对电缆起固定和支撑作用的电缆附件设备。电缆金具固定在安装面上，但并不依赖于电缆安装面[5]。电网短路时，载流导体将承受非常巨大的电动力，而电缆金具使得电缆固定，从而防止在短路电流情况下电缆电动力损伤电缆，保证电网安全稳定的运行[6]。对于短路电流来说，其产生的机械应力效应远大于热效应[7]。因此，对高压大截面电缆金具短路电动力机械应力的研究具有非常重要的实际意义。

本文采用暂态短路电流计算方法和有限元法，分析短路电动力的计算原理，并根据计算原理得到短路电动力计算公式。考虑电缆蛇形敷设(蛇形敷设主要是为了吸收电缆线路热胀、冷缩量，同时可减缓短路电动力机械响应)、导体外层介质缓冲作用和短路发生后电缆位移偏转量等因素，引入系数K1和K2系数对作用在电缆金具上的短路电动力进行修正。基于ANSYS建立了电缆金具系统三维有限元计算模型，分别研究了敷设跨距和电缆相间距对金具应力场的影响。

1暂态短路电流计算

为分析高压大截面电缆金具短路电动力机械应力，必须找出系统中可能出现的最严重的短路电流。在电力系统各类短路故障中，三相短路时产生的短路电流最为严重。三相短路时，暂态过程中短路电流通常包括非周期分量与周期分量两部分。周期分量被称为稳态分量，取决于系统短路时的阻抗；非周期分量被称为暂态分量，取决于发生短路时电源电压相位。

以“无穷大容量”供电系统为例，当电缆三相母线发生对称短路，则短路时认为电压不变、短路电流周期分量不衰减而非周期分量是衰减的，且非周期分量与短路发生瞬间与电压的相位角有关，则三相母线上短路电流为[8]

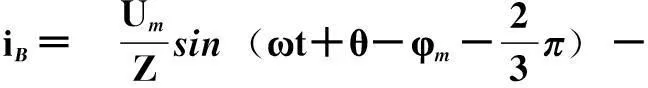
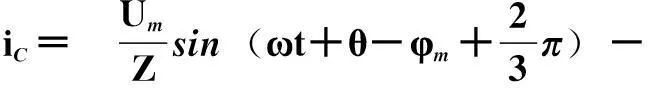
(1)

式中，Um为相电压幅值；Z为每相回路从电源至短路点的等效短路阻抗，Z=R+jX1；ω为电源角频率；τa为短路回路的时间常数，τa=L/R；θ为相电压的初相位角，一般称为合闸相角；φm为短路电流与电压之间的相角或短路阻抗角，φm=arctan(ωL/R)。

校验电气设备的电动力稳定性应采用短路电流最大可能瞬时值进行计算，即短路冲击电流，用ish表示。当电路参数已知时，短路电流周期分量的幅值是一定的，而非周期分量则按指数规律单调衰减。因此，非周期分量电流初值越大，暂态过程中短路全电流瞬时值就越大。图1为简单三相电路短路时的相量图。

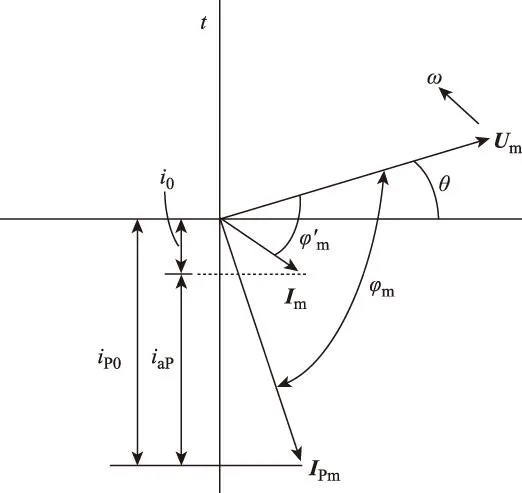
图1　简单三相短路相量图Fig.1　The phasor diagram of simple three-phase short circuit

图1中，Im、IPm分别为短路前电流幅值和短路电流周期分量的幅值，它们在时间轴t上的投影i0、 iP0分别为短路前电流和短路后周期电流的瞬时值。根据电路开闭定律，电感中的电流不能突变，因此电路中必须产生一个非周期自由电流，即非周期电流的初值为iaP。 由图1可知，要使非周期电流有最大值，应满足当Im-IPm在t=0时与时间轴平行。一般电力系统中，由于短路回路阻抗比电阻大得多，即ωL≫R， 故可近似认为φm≈90 ℃， 即当短路前电路处于空载状态，且短路发生时电源电动势恰好过零，非周期电流具有最大初值。因此，短路电流的最大瞬时值在短路发生后约半个周期时出现，即t=0.01 s时，三相短路冲击电流ish为

ish=IPm(1+e-0.01/τa)=KshIPm

Ksh=(1+e-0.01/τa)

(2)

式中，Ksh为短路电流冲击系数，表示冲击电流为短路电流周期分量幅值的多少倍，当时间常数由零变化到无穷大时，Ksh的取值范围为1≤Ksh≤2。

以双桥子-桃乡220 kV双回线路新建工程电缆段为例，电缆型号为YJZW02-Z 127/220 2500 mm2，线路总长1.43 km，敷设于隧道。根据该回路各参数计算得，该回路最大冲击电流有效值为50 kA，短路时间为0.2～2 s。

2暂态短路电动力计算

图2为电缆受力示意图。由图2可知，令三相电流为同向，电缆采用“一”字形排列方式，电缆任意一相导体上的电动力为中间相及另一边缘相电缆导体中电流对其作用之和，但A、C两相电缆导体间的距离是它们与B相电缆导体间距离的两倍。由电动力公式可得，作用在A、B、C三相电缆导体上的电动力分别为

(3)

式中，C1、 C2、 C3表达式为

(4)

式中，(Kh)A·B， (Kh)A·C， (Kh)B·C分别为A、B，A、C和B、C相电缆导体间的回路因素；Kc为截面因素。

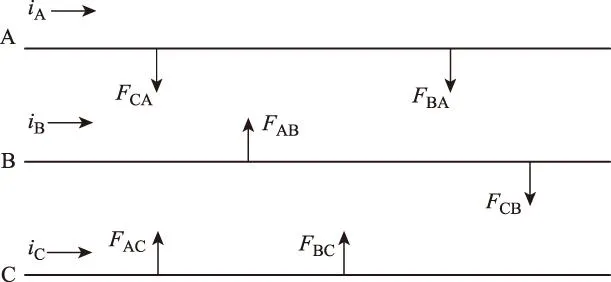
图2　三相电缆受力示意图Fig.2　The stress diagram of three-phase cable

因为电缆采取“一”字形对称排列，各相电缆截面积相同，故有C1=C3=2C2， 将式(1)带入式(3)中，其中令IPm=Um/Z， 可化简得FA、 FB为

FB=FAB+FCB

=C1(iAiB-iBiC)

(5)

作用在A相或C相上的电动力为

FA=FBA+FCA

=C1(iAiB+0.5iAiC)

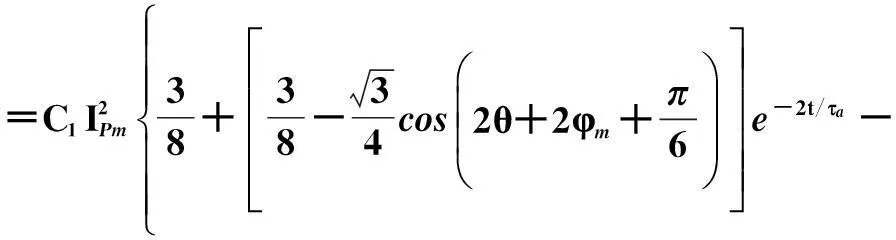
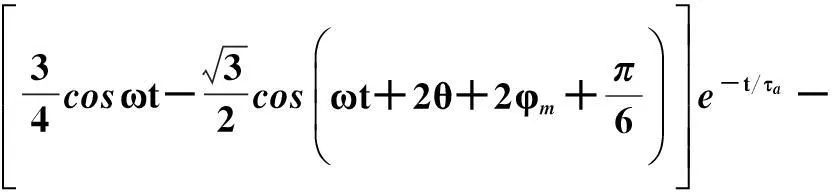
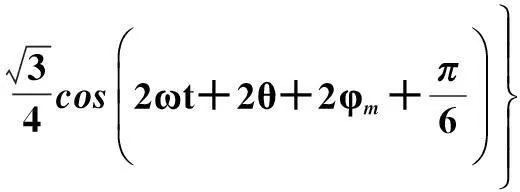
(6)

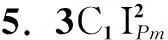
值小于采用短路冲击电流计算所得短路冲击电动力的值)，即在设计高压大截面电缆金具时，金具需满足B相载荷要求。

校核电器设备电动稳定性时，需采用短路冲击电流峰值进行计算，当t=0.01 s时，B相短路电流瞬时值最大即短路冲击电流，此时相短路电动力也达到最大值，短路电动力为

(7)

式中，ish为短路冲击电流，A；l为平行导线长度或两支撑物之间的距离，m；a为两导体中心的距离，m；Kf为导体截面的形状系数，对于圆形、管形导体，Kf=1.0，对其他截面导体，当l≫a， Kf≈1.0。

由以上分析可知，当发生三相短路时，B相电缆所受斥力和吸力方向相反，电缆将发生振动，通过振动作用将短路电动力作用在金具上。由于交联聚乙烯绝缘电缆内部包含内半导电包带、导体屏蔽层、绝缘层、绝缘屏蔽层、半导电缓冲带、波纹铝护套以及外护套，导体外共含有7层介质，同时考虑电缆蛇形敷设以及由短路冲击电动力产生的电缆位移偏转量等因素[9，10]，因此，交联聚乙烯绝缘电缆中所产生的短路电动力作用在金具机械响应缓慢，由于电缆外7层介质的缓冲作用，任何初始瞬态故障电流在导体上产生的短路电动力不可能在金具上产生同样大小的力。图3为 B相电缆产生的短路冲击电动力在金具上所产生的作用力示意图。

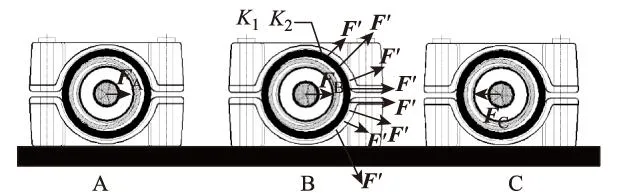
图3　B相电缆对金具作用力示意图Fig.3　Force diagram of the B phase cable to the cleat

图3中标出了三相导体受力分别为FA、FB、FC。由机械振动学可知[11，12]，K1为工频分量(50 Hz)修正系数，表达式为

(8)

K2=x′{1+(2Crf)2}1/2

(9)

式中，x′为两倍工频分量振幅；Cr为电缆阻尼比；f为频率比；F′为短路电流作用在金具上的力。

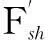
(10)

由试验数据可知[9]，双桥子-桃乡220 kV双回线路电缆隧道实际敷设跨距为l=1.5 m时，K1为0.32。由于电缆内部结构复杂使得其机械性能参数(如阻尼、自由度)难以估计，因此确定K2的值相当困难，通过试验测试手段推荐在工程应用中K2值一般取作0.5[9，10]。

由以上参数计算可得，当t=0.01 s时，双桥子-桃乡220 kV的双回线路作用在金具上的短路冲击电动力为

=1 090.91N

(11)

3ANSYS有限元计算模型

根据隧道敷设电缆金具安装模型建立相应的三维有限元计算模型，双桥子-桃乡220 kV电缆隧道敷设如图4所示。因为B相受力最大，所以只需对B相电缆固定和支撑金具进行研究，建立的三维有限元计算模型如图5所示。所采用固定金具和支撑金具参数如表1和表2所示。

图4　双桥子-桃乡220kV电缆隧道敷设示意图Fig.4　The diagram for 220 kV cable transmission line called Shuang Qiaozi-Tao Xiang

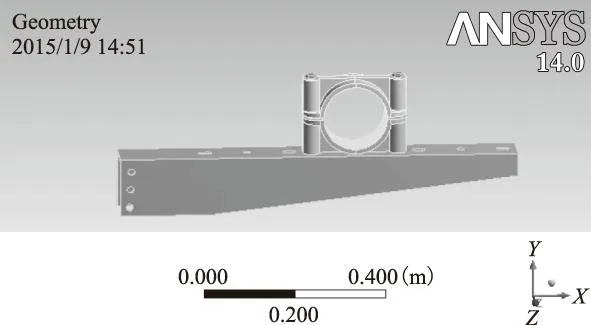
图5　电缆固定金具及支撑金具三维模型Fig.5　3D model of power cable and cable cleat

(单位：mm)

表2　支撑金具结构参数

采用四面体单元分别对模型各部件进行自适应的网格划分，共有20 835个单元。模型的有限元剖分结果如图6所示。

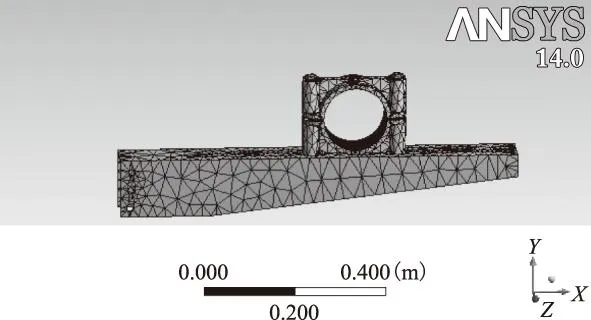
图6　剖分结果图Fig.6　The meshing result

4短路电动力场计算结果及讨论

根据ANSYS有限元计算模型，采用ZL2(T4及以上)铸造铝合金作为固定金具材料；支撑金具和螺栓材料为热镀锌钢板，材料代号为S220GD+ZF，对该电缆金具系统承受短路电动力时进行分析。短路时间为0.2～2 s，仿真计算时设置当t=0.01 s时力达到最大值，ANSYS载荷近似以线性加载。

对电缆蛇形敷设跨距和电缆相间距对电缆金具应力场的影响进行了研究。图7、图8分别为电缆金具整体应力分布图和支撑金具及螺栓上的应力分布图。

图7　电缆金具整体应力分布图Fig.7　The stress distribution of cable cleats.

图8　支撑金具和螺栓应力分布图Fig.8　The stress distribution of support cleats and bolt

从图7和图8中可看出，固定金具在其最薄的上下壁中间所产生的应力最大，即短路电动力最易使得固定金具在上下表面变形；支撑金具在与螺栓固定处及与壁上角钢连接处产生的应力最大，短路电动力很容易使得螺栓与支撑金具连接处螺母松动，并有可能使螺栓发生变形，固定松动很容易导致电缆损伤使得电缆系统发生故障；从图中还可看出在螺杆中间位置所受到的应力是整个电缆金具系统最大位置，因此在考虑系统形变时应首先考虑该位置，系统中短路电动力最易导致该位置发生变形甚至拉断。

4.1电缆蛇形敷设跨距对应力场的影响

隧道电缆蛇形敷设跨距对电缆短路电动力影响非常大。对敷设跨距l分别为1.5 m、1.8 m、2.1 m、2.4 m、2.7 m时金具应力场分布情况进行了研究，图9为电缆隧道蛇形敷设示意图，表3为每个跨距所对应作用在固定金具上的短路电动力。

图9　电缆隧道蛇形敷设示意图Fig.9　The diagram of serpentine layingin the cable tunnel

l/m1.51.82.12.42.7F'sh/N1090.911309.091527.271745.451963.63

根据GB/T 1173—1995和GB/T 2518—2008[13，14]，ZL2系列铸造铝合金(T4及以上)最小抗拉强度为205 MPa，电缆线芯铜导体最小抗拉强度为220 MPa，结构钢最小抗拉强度为330 MPa。

金具应力随跨距变化如图10所示，随着敷设跨距l增大，在螺栓、支撑金具及固定金具上最大应力均增大(近似为线性关系)。通过仿真计算可知，螺栓上的应力数值比支撑和固定金具上的数值高一个数量级，因此螺栓是该电缆金具系统最易发生变形或拉裂的位置，通过定性和定量的研究都证实了其与理论推导的正确性。当敷设跨距l=2.7 m时，螺栓的螺杆中间位置应力最大值为327.07 MPa，与结构钢的最小抗拉强度330 MPa非常接近，考虑到电缆在短路电动力情况下的安全系数和强度最大要求，因此双桥子-桃乡220 kV的双回线路新建工程电缆段及类似电缆工程敷设跨距应满足l≤2.7 m。图11为敷设跨距螺栓上产生的最大应力。

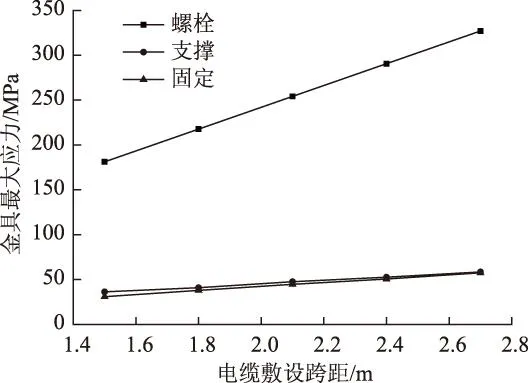
图10　金具应力随跨距变化图Fig.10　Cable cleat stress changed with span spacing

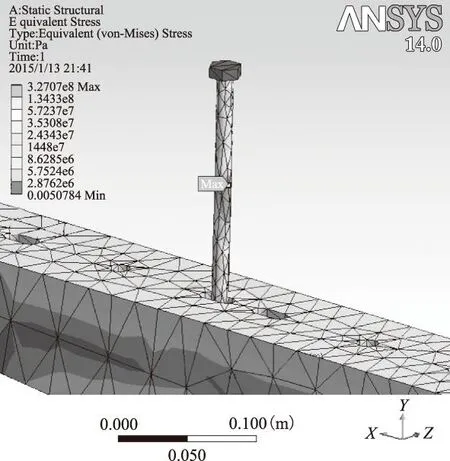
图11　螺栓最大应力示意图Fig.11　The maximum stress value in the bolt

4.2电缆相间距对应力场分布的影响

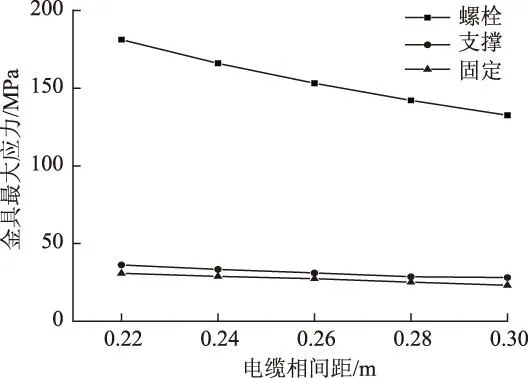
电缆相间距不仅影响电缆载流量，同样对短路电动力起着至关重要的作用。由理论分析可知，电缆相间距增大，将减弱电缆相互之间电磁感应作用，电缆损耗降低，使得电缆载流量增大且短路电动力也将减小。对于双桥子-桃乡220 kV的双回线路新建工程电缆段，给出参考相间距为0.22 m，对相间距分别为0.22 m、0.24 m、0.26 m、0.28 m以及0.30 m时金具系统应力分布进行了研究。表4为相间距所对应短路电动力。

表4　不同相间距所对应短路电动力

电缆采取隧道敷设方式，由于隧道内敷设空间有限，且隧道内采取多回路敷设，因此有效利用隧道内部空间同时又不影响电缆正常运行成为当前电缆敷设中需重点研究的问题。

图12为金具应力随电缆相间距变化图。由图可知，金具应力随着相间距增大而减小，这与理论分析相吻合。螺栓应力高于支撑和固定金具一个数量级，因此在该系统中螺栓最易变形或拉断。考虑金具结构尺寸，仿真所得相间距对应螺栓最大应力均小于螺栓的最大应力333.15 MPa。但考虑电缆之间电磁感应和电缆散热同载流量的关系，对于实际工程中敷设的电缆相间距建议在0.28～0.3 m。因此对于双桥子-桃乡220 kV的双回线路新建工程电缆段以及类似电缆工程为“一”字形排列时，推荐电缆相间距0.28 m

图12　金具应力随电缆相间距变化图Fig.12　Cable cleat stress changed with phase spacing

5结论

根据对高压大截面电缆金具短路电流的电动力机械应力分析可得以下结论：

1)基于ANSYS仿真结果分析，螺栓螺杆中点处所产生应力值最大，其数值高于支撑和固定金具一个数量级，是该电缆金具系统中最易被短路电动力变形或拉裂位置。

2)研究了跨距对金具应力场分布的影响。通过与螺栓材料抗拉强度作比较，最后得出对于双桥子-桃乡220 kV的双回线路新建工程电缆段以及类似电缆工程为“一”字形排列的敷设跨距应满足l≤2.7 m。

3)研究了电缆相间距对金具应力场分布的影响。通过与螺栓材料抗拉强度作比较，并且考虑电缆之间电磁感应和电缆散热与载流量关系，最后得出对于双桥子-桃乡220 kV的双回线路新建工程电缆段以及类似电缆工程为“一”字形排列的电缆相间距应满足0.28 m≤a≤0.30 m。

参考文献

[1]Labridis D，Dokopoulos P.Finite element computation of eddy current losses in nonlinear ferromagnetic sheaths of three-phase power cables[J].IEEE Transactions on Magnetics，1994，30(4)：1407-1415.

[2]Wang X，Wang C C，Wu K.An improved optimal design scheme for high voltage cable accessories[J].IEEE Transactions on Dielectrics and Electrical Insulation，2014，21(1)：5-15.

[3]Ruger W.Mechanical short-circuit effects of single-core cables[J].IEEE Transactions on Power Delivery，1989，4(1)：68-74.

[4]BS EN 50368：Cable Cleats for Electrical Installations[S].British：European Standard，2003.

[5]Damell C A ，Bacon M L ，Shaw R A.Cable cleats-a global technique to protect three-phase single conductor cables during short-circuits[C]//Petroleum and Chemical Industry Technical Conference，Los Angeles，2004：143-150.

[6]Heinhold L.Power Cables and Their Application[M].Weinheim：Wiley-VCH，1990.

[7]Booth A W ，Hanekom A .Why correctly engineered cable cleats are vital for effective power system protection[C]//The 10th IET International Conference on Developments in Power System Protection，Manchester，2010：1-5.

[8]冯金光，王士政.发电厂电气部分[M].北京：中国水利水电出版社，2002.

[9]Foulsham N ，Metcalfe J C ，Philbrick S E.Proposals for installation practice of single-core cables[J].Proceedings of the Institution of Electrical Engineers，1974，121(10)：1168-1174.

[10]Attri N S，Edgar J N. On the response of bus bars on elastic supports subjected to a suddenly applied force[J].IEEE Transactions on Power Delivery，1967，86(5)：636-650.

[11]金斯伯格.机械与结构振动：理论与应用[M].白化同，李俊宝，译.北京：中国宇航出版社，2005.

[12]Den Hartog J P.Mechanical Vibrations[M].New York：McGraw-Hill，1956.

[13]GB/T 1173—1995 铸造铝合金[S].北京：中国标准出版社，1995.

[14]GB/T 2518—2008 连续热镀锌钢板及钢带[S].北京：中国标准出版社，2008.

刘航宇男，1990年生，硕士研究生，研究方向为高电压技术与电力设备故障诊断。

E-mail：623141161@qq.com(通信作者)

刘念男，1956年生，教授，硕士研究生导师，研究方向为高电压技术与设备故障诊断。

E-mail：liunianww@163.com

作者简介

中图分类号：TM757.3

收稿日期2015-01-24改稿日期2015-04-24