基于厚尾均值广义自回归条件异方差族模型的短期风电功率预测
陈 昊 万秋兰 王玉荣
(东南大学电气工程学院 南京 210096)
基于厚尾均值广义自回归条件异方差族模型的短期风电功率预测
陈昊万秋兰王玉荣
(东南大学电气工程学院南京210096)
摘要风电功率预测准确度的提高对提高电力系统调度效率具有重要的作用。基于对风电功率时间序列波动性的研究,推广了一种厚尾均值广义自回归条件异方差(GARCH-M)族短期风电功率预测模型,同时,基于波动补偿项的不同形式,将模型拓展为多种类型的厚尾GARCH-M模型。该类模型能够捕捉风电功率时间序列波动性与其条件均值的直接关系,并能够有效刻画具有高峰度特征的实际风电功率序列的厚尾效应,使风电预测准确度提高。结合江苏地区风电场风电功率实际数据,对所提厚尾GARCH-M模型进行了参数估计,论证了存在于风电时间序列中的GARCH-M效应和厚尾效应,给出了风电功率均值和条件方差的预测方案。算例分析结果验证了所提方法的可行性和有效性,表明了考虑厚尾特征的GARCH-M族模型短期预测效果满意。
关键词:均值广义自回归条件异方差模型风电功率预测厚尾效应波动补偿系数
Short-Term Wind Power Forecast Based on Fat-Tailed Generalized Autoregressive Conditional Heteroscedasticity-in-Mean Type Models
ChenHaoWanQiulanWangYurong
(School of Electrical EngineeringSoutheast UniversityNanjing210096China)
AbstractImproving the precision of wind power forecasting can be helpful to the increase of dispatch efficiency.In this paper,based on the the investigation on the intrinsic volatility of wind power time series,the fat-tail generalized autoregressive conditional Heteroscedasticity (GARCH) in mean type short term wind power forecasting models are generalized.Based on different formulations of volatility compensation items,several types of the fat-tail GARCH-M models are derived.The proposed models can capture the direct relationship between the volatility of wind power time series and its conditional mean.Furthermore,the models can depict the fat-tail effect in the practical wind power time series with leptokurtosis feature to improve the forecasting performance.In the case study,by means of the historical coastal wind power data of Jiangsu wind farm,the parameters of the proposed models are estimated,the GARCH-M effect and the fat-tail effect in the wind power time series are verified,and the conditional mean and conditional variance of the wind power are forecasted.Case study results clearly illustrate the validation and effectiveness of the proposed methods.And it is clearified that the GARCH-M model with the consideration of fat-tail effect is effective to provide satisfying forecasting results.
Keywords:Generalized auto-regressive conditional Heteroskedasticity (GARCH)-in-mean model,wind power forecast,fat tail effect,volatility compensation coefficient
0引言
清洁能源的开发和利用既是环境治理和生态保护的重要措施,也是整个能源供应系统的有效补充手段。其中,风能是近年来全球发展最为迅猛的可再生能源,也是增长最快的发电能源。《2013中国风电发展报告》指出[1],截止到2012年底,中国新增风电装机容量45 GW,同比增加10%;全球风电累计装机容量达到282.5 GW,同比增加19%。基于丰富的风电资源及人们对绿色能源的期许,未来风电发展仍将保持迅猛上升势头,2015年底我国风电并网总装机容量将达到1亿kW,2020年累计装机容量将超过2亿kW。
风电场风电功率的预测研究是调度运行部门安排调度计划、计算电力系统稳定性等问题的基础条件[2-6]。随着风电功率并网比例不断上升,风电功率波动性的影响日益受到人们关注,如何分析风电波动特征,进而提高大规模风电场风电功率并网后的预测准确度,是亟待解决的重要研究课题。
目前,一些风电预测方法和模型已被提出并应用,如物理模型[2]、经典时间序列模型(Autoregressive Integrated Moving Average Model,ARMA)[3-5]、广义自回归条件异方差(Generalized Autoregressive Conditional Heteroskedasticity,GARCH)模型[7]、神经网络模型[7,8]、支持向量机[9]以及混合模型[10-12]等。其中,时间序列模型因其建模技术成熟和应用方便,在风电预测方法占有重要的一席之地。文献[3]讨论了基于ARMA模型为代表的经典时间序列模型的风速和风电预测方法。文献[4]讨论了考虑噪声背景的ARMA风电预测模型。文献[5]讨论了基于一种ARMA变体——f-ARIMA模型的风速预测方法。改进的经典时间序列模型能在一阶矩层面较好地描述风电时间序列,但受制于模型结构难以对风电序列高阶矩特征做进一步的发掘。以GARCH族模型为代表的现代时间序列模型长于描述高阶矩信息。文献[6]报道了风电功率时间序列的波动集聚效应,提出了基于经典GARCH风电预测模型。然而,现有研究只给出了分析风电时间序列波动性的基本框架,对风电波动特性的研究尚不充分,较多重要的波动性特征尚缺乏实用的理论分析手段。
为进一步分析风电时间序列各种波动性特征,充分发掘风电功率时序的高阶矩信息以提高预测准确度,本文基于厚尾的均值GARCH(GARCH-in-Mean,GARCH-M)风电预测模型,捕捉风电功率时间序列波动性与其条件均值的直接关系,分析了风电时序GARCH-M效应和厚尾效应两种波动性特征,最后通过实际数据对模型预测能力进行了验证和分析。
1GARCH-M模型的提出
1.1GARCH模型
ARCH模型[13]开创了时间序列高阶矩分析的新框架。文献[14]推广了ARCH模型,提出GARCH模型。GARCH族模型能够有效刻画时间序列条件方差的时变特征,是刻画时间序列波动性的经典主流模型之一。
一个典型的GARCH模型由条件均值方程和条件方差方程组成,即
均值方程
(1)
方差方程
(2)
1.2TSGARCH与PGARCH模型
经典GARCH模型有效地刻画了很多领域时间序列的波动性,但由于经典GARCH模型以ht为中心构建式(2),难以和某些实际数据契合。因此,Taylor提出了TSGARCH模型[15],以条件标准差为中心重新构建式(2),得到TSGARCH模型的条件方差方程为
(3)

为更灵活地构建式(2),Z.Ding又提出了PGARCH模型[16],可通过调整势参数γ,以ht的某个函数为中心构建式(2),进一步增强了刻画风电时间序列波动性的灵活性。PGARCH模型的条件方差方程形如
(4)
式中,势参数γ>0。 易验证,当γ=2时,PGARCH模型退化为GARCH模型。
1.3GARCH-M族模型
很多场合的时间序列波动性和其条件均值存在直接的相关关系[17],即存在GARCH-M效应。此时,文献[17]使用GARCH-M模型捕捉这种相关关系。
1.3.1GARCH-M模型
一个典型的GARCH-M模型由条件均值方程和条件方差方程组成,形式如下
均值方程
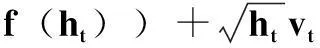
(5)
方差方程
(6)
式中,均值方程中的E(δ f(ht))是波动补偿项δ f(ht)的数学期望;δ为波动补偿系数,用于表征时间序列波动性对条件均值直接影响的强弱程度。
与GARCH模型相比,GARCH-M模型在均值方程中引入了波动补偿项δ f(ht)的影响因素,能够刻画时间序列的波动性与条件均值的关系。若参数估计结果中δ显著不为0,则说明时间序列波动性和其条件均值存在直接的相关关系;相反,若参数估计结果中δ=0, 则说明GARCH-M效应不显著,此时GARCH-M模型退化为 GARCH模型。
模型均值方程中,f(ht)用以刻画时间序列波动性对条件均值的直接影响,其经典形式有如下三种。
f(ht)=ht
(7)
(8)
f(ht)=loght
(9)
因此,本文基于所采用的不同波动补偿项形式,得到三种GARCH-M类模型:将采用f(ht)设定为式(7) 的GARCH模型称为第一型GARCH-M模型,记为GARCH-M1模型[6];类似地,f(ht)设定为式(8)或式(9) 的GARCH-M模型分别记为GARCH-M2模型或GARCH-M3模型[6]。
1.3.2TSGARCH-M模型与PGARCH-M模型
按照GARCH-M的思路,可将TSGARCH模型和PGARCH模型推广为TSGARCH-M模型和PGARCH-M模型以更好地刻画风电时间序列的波动性。
TSGARCH-M模型形如
(10)
PGARCH-M模型形如
(11)
易知,若波动补偿系数δ≠0, 则说明时间序列波动性与条件均值存在直接的相关关系被模型所刻画;相反,若δ=0, 则TSGARCH-M模型将退化为TSGARCH模型;类似地,PGARCH-M模型将退化为PGARCH模型。
2厚尾GARCH-M族模型
2.1vt分布的推广
风电功率时间序列波动剧烈,经常呈现出高峰度特征。经典GARCH-M族模型中vt采用的正态分布虽然在一定程度上可以刻画风电时间序列的这种现象,但在某些高峰度特征显著且呈现出极厚的厚尾(fat tail)特征的场合,正态分布有时无能为力。为进一步增强刻画风电序列厚尾的能力,可以考虑将式(5)中的vt由服从正态分布扩展成为服从厚尾分布。对vt分布的扩展,有利于提高实际风电功率预测系统的预测准确度。
本文算例中分别采用了两种厚尾分布形式:标准t分布和标准广义误差分布(Generalized Error Distribution,GED)[18]。其中,GED的概率密度函数形为
(12)
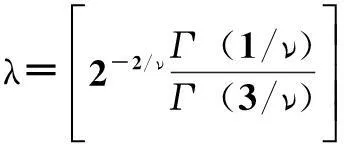
GED、t分布和正态分布概率密度如图1所示,其尾部特征的差别见图1的局部放大图。可见GED和t分布能够刻画分布的厚尾特征。
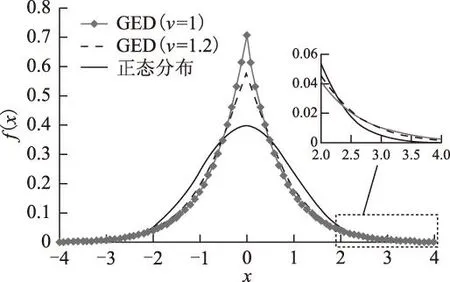
图1 GED的概率密度Fig.1 The probability density of GED
2.2ARCH效应的检验方法
判断一个序列是否存在ARCH效应是进行GARCH族模型建模的前提之一。本文采用ARCH效应检验方法为拉格朗日乘子(Lagrange Multiplier,LM)检验和鲁棒MQ(robust Modified Q)检验。
2.3厚尾GARCH-M族模型的参数估计
本文采用条件对数极大似然估计方法获取厚尾GARCH-M族模型的参数估计,同时使用Marquardt算法进行迭代控制。
3算例分析
3.1数据
算例分析基于江苏北部某沿海风电场风电数据建模。样本空间为2013年4月1日~4月7日的风电功率数据,样本间隔为5 min(共计2 016个样本点)。根据该样本建立厚尾GARCH-M族模型,并分析其GARCH-M效应与厚尾效应,预测2013年4月8日、4月9日的风电功率,考察厚尾GARCH-M短期风电功率预测模型的预测能力。
3.2序列检验与模型参数估计
3.2.1平稳性检验与ARCH效应检验
运用ADF(augmented dickey-fuller)检验和PP(phillips-perron)检验考察风电序列Yt的平稳性。两种检验的结果一致表明Yt不平稳,进而对风电时间序列作一阶差分,即
yt=Yt-Yt-1
(13)
再次运用ADF 检验、PP检验验证差分序列yt的平稳性,两种检验一致表明即使在1%的水平上亦应该拒绝原假设,即yt是平稳的,满足建模前提条件。
分析yt序列自相关函数和偏自相关函数,建立可行阶数的ARMA模型集合,进而计算集合中各ARMA模型的赤池信息准则(Akaike Information Criterion,AIC)、贝叶斯信息准则(Bayesian Information Criterion,BIC),筛选出阶数最为适当的ARMA(4,5),作为初始ARMA模型。
运用LM检验和鲁棒MQ检验考察初始ARMA模型的εt,两种的检验结果一致表明,风电时间序列存在显著的高阶ARCH效应,满足GARCH族模型的建模要求。
3.2.2厚尾GARCH-M模型的参数估计
基于提出的厚尾GARCH-M风电预测模型,采用文献[19]的定阶方法,分别采用t分布及GED形式,将模型确定为ARMA(4,5)-GARCH(1,1)-M-t和ARMA(4,5)-GARCH(1,1)-M-GED,简记为GARCH-M-t和GARCH-M-GED。易知,模型条件均值方程为
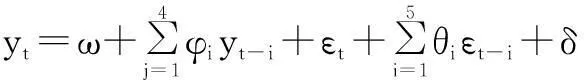
(14)
考虑到f(ht)可以取为式(7)、式(8)或式(9),厚尾分布取为t分布或GED,联立式(16)、式(6),共可建立6种厚尾GARCH-M模型。对6种模型运用条件对数极大似然估计,获得厚尾GARCH模型的参数估计见表1。
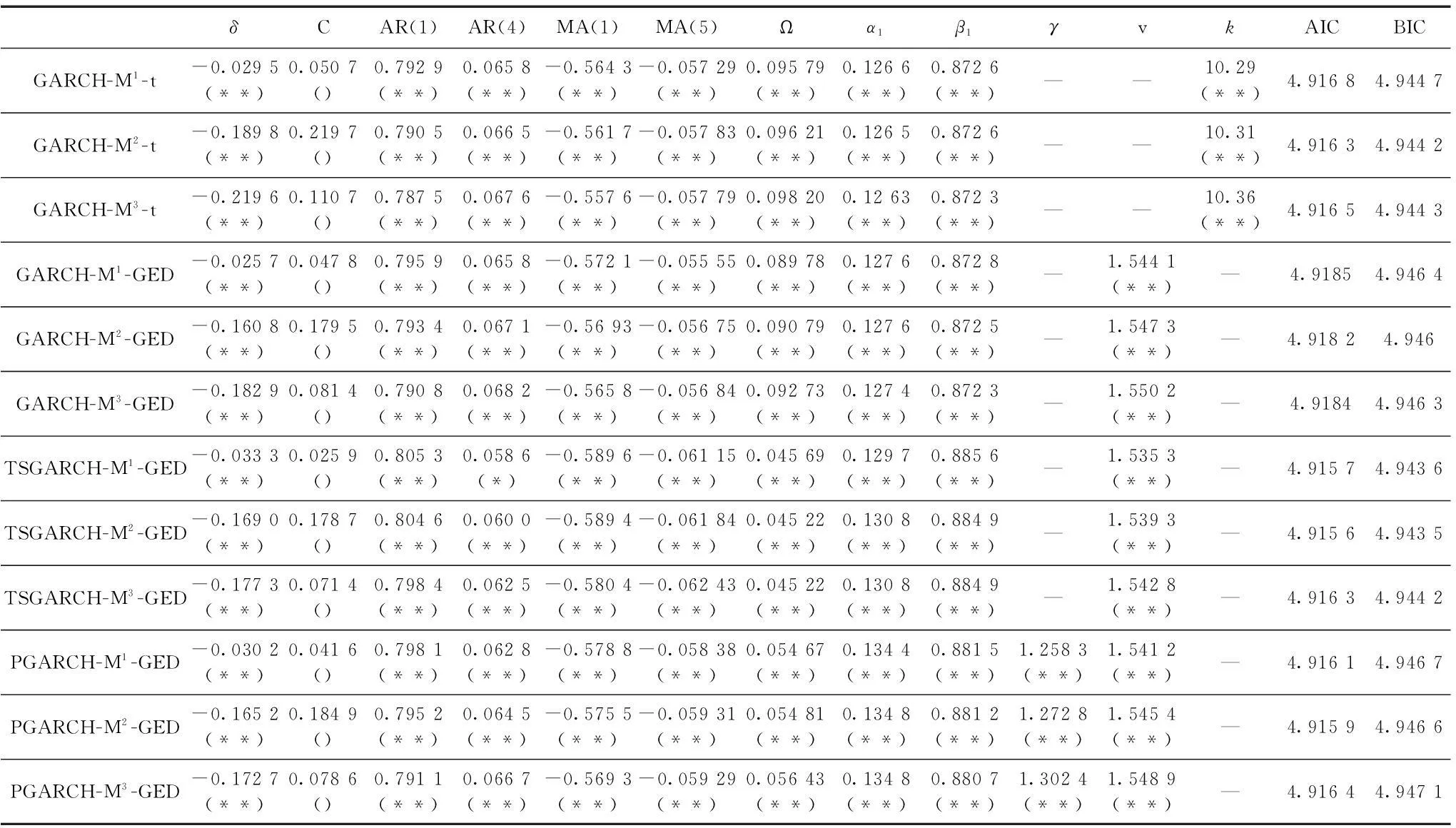
表1 厚尾GARCH-M模型的参数估计
注:括号内为参数的显著水平,*表示在10%水平下显著,**表示在5%水平下显著,k为t分布的自由度参数。
3.2.3厚尾TSGARCH-M和厚尾PGARCH-M的参数估计
进一步将条件方差方程的结构加以推广,并引入GED,建立三种ARMA(4,5)-TSGARCH(1,1)-M-GED模型和三种 ARMA(4,5)-PGARCH(1,1)-M-GED模型,简记为TSGARCH-M-GED和PGARCH-M-GED模型。使用条件对数极大似然估计获得参数估计,俱见表1。
从表1可得到以下三点结论:
(1)所有GARCH-M-GED模型的GED形状参数均显著且有ν<2, 正符合GED拥有厚尾的情形,所有GARCH-M-t模型的t分布的自由度参数均显著,亦呈现出厚尾的特征。
(2)所有厚尾GARCH-M模型的波动补偿系数均显著,且均为负值,考虑到ht恒正,GARCH-M1模型和GARCH-M2模型中,波动补偿项δ f(ht)对风电功率均值有负向的影响。进一步考虑本算例中ht几乎始终大于1,log(ht)几乎始终为正,因此,GARCH-M3模型中,波动补偿项δ f(ht)在总体上对风电功率均值亦有负向的影响。
(3)尽管各种厚尾GARCH-M模型的结构存在差异,但均值方程的所有参数的系数符号方向均一致,且数值上也较为接近,反应了不同模型捕捉到的条件均值是接近的。
3.3GARCH-M效应分析
为进一步从微观变化角度对时间序列GARCH-M效应进行检验,下面以第一型GARCH-M-GED模型和第一型PGARCH-M-GED为代表,使用滚动子样本检验分析风电功率时间序列GARCH-M效应在全样本时间尺度内参数结构的微观变化。
滚动子样本检验分析的计算条件为:在选定的滚动样本长度M之后,首先,从样本空间中提取连续M个样本数据构成一个单向队列,进行基于该数据集的模型参数估计。然后,从全样本空间中提取接下来1小时的数据(共计12个样本点)加入队列;同时,将队列中的前12个样本点移除如图2所示,保证队列中始终包含M个连续样本数据空间,并进行新数据集的模型参数估计。

图2 滚动样本检验分析法Fig.2 Rolling sample test
易知,若队列最初的样本集为全样本空间的最早72 h(共计M=864个观察值)数据,则滚动样本检验分析法共计得到97个子样本。分别对97个子样本建立GARCH-M-GEDi(i=1,2,…,97)模型和PGARCH-M-GEDi(i=1,2,…,97)模型,并估计其参数。
提取子样本模型GARCH-M-GEDi模型和PGARCH-M-GEDi模型中δ的参数估计值,得到δ∈[-0.067 762,-0.020 868],绘制动态波动补偿系数曲线如图3所示。
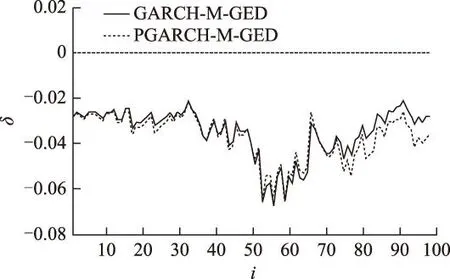
图3 动态波动补偿参数曲线Fig.3 Dynamic volatility compensation parameter curve
由图3可见:
(1)尽管基于不同的子样本建模,但97个GARCH-M-GED模型的波动补偿系数始终都为负值,说明条件方差在全样本周期内均有促使风电功率的条件均值下降的作用,而且这种效应具有较明显的持续性。
(2)各子样本PGARCH-M-GED模型的波动补偿系数也均为负值。尽管两种厚尾GARCH-M模型结构有别,但两个模型的动态波动补偿参数曲线走势十分近似。可见,本算例中风电功率时间序列的GARCH-M效应是显著而且稳定的,两种模型关于条件方差对条件均值影响的结论是一致的。
3.4厚尾效应分析
进而运用滚动子样本方法从微观变化角度对风电时间序列厚尾效应进行检验,估计子样本模型GARCH-M-GEDi模型和PGARCH-M-GEDi(i= 1,2,…,97)模型的形状参数ν。
图4给出了所有子样本模型中广义误差分布的形状参数时变曲线和相应的95%置信区间。虽然97个厚尾GARCH模型分别依据的是不同子样本,但从图4中可以清晰地看出,形状参数始终小于2,即时间序列条件分布的尾部始终保持着显著厚于正态分布的厚尾状态,未随子样本变化而改变。
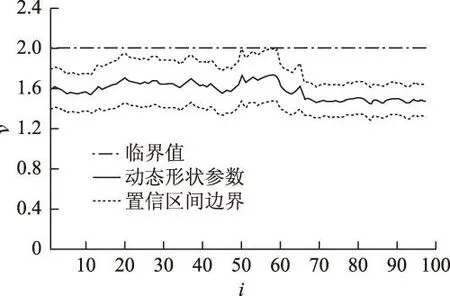
图4 GARCH-M-GED模型的动态形状参数曲线 Fig.4 Dynamic shape parameter curve in GARCH-M-GED model
类似地,可绘制PGARCH-M-GED模型的动态形状参数曲线及相应的95%置信区间如图5所示。
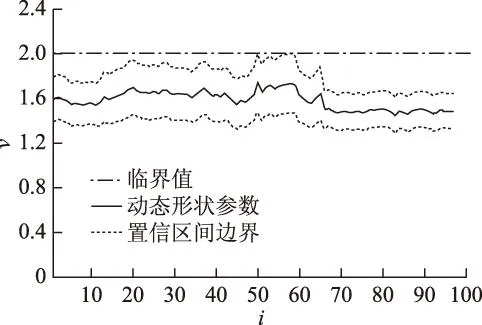
图5 PGARCH-M-GED模型的动态形状参数曲线 Fig.5 Dynamic shape parameter curve in PGARCH-M-GED model
易见,虽然两种厚尾GARCH-M模型在模型结构上有着明显的区别,在所有子样本中,两种模型的GED形状参数ν始终一致性地小于2,甚至图4和图5的动态形状参数曲线走势都极为接近。此亦表明两种厚尾GARCH-M模型一致判别出全样本周期内风电时间序列存在显著的厚尾效应。
3.5模型预测结果
基于模型的参数估计结果,预测实际风电功率,考核厚尾GARCH-M族风电功率模型的预测能力。最后由差分序列复原出风电功率预测值,预测模型为
(15)
分别使用上述模型预测苏北某沿海风电场往后2天(共576个样本点)的风电功率。
采用方均误差ERMS(Root Mean Squared Error,RMSE),平均绝对误差EMAE(Mean Absolute Error,MAE)和平均绝对百分误差EMAPE(Mean Absolute Percentage Error,MAPE)对风电预测结果进行评价。三种预测精度度量指标的表达式如下
(16)
(17)
(18)
12种厚尾GARCH-M族风电功率模型预测结果的对比归纳见表2。另外,持续模型(TP)、ARMA模型、经典GARCH模型、TSGARCH模型、PGARCH模型及其他9种GARCH-M族模型作为对照模型,预测结果亦见表2。
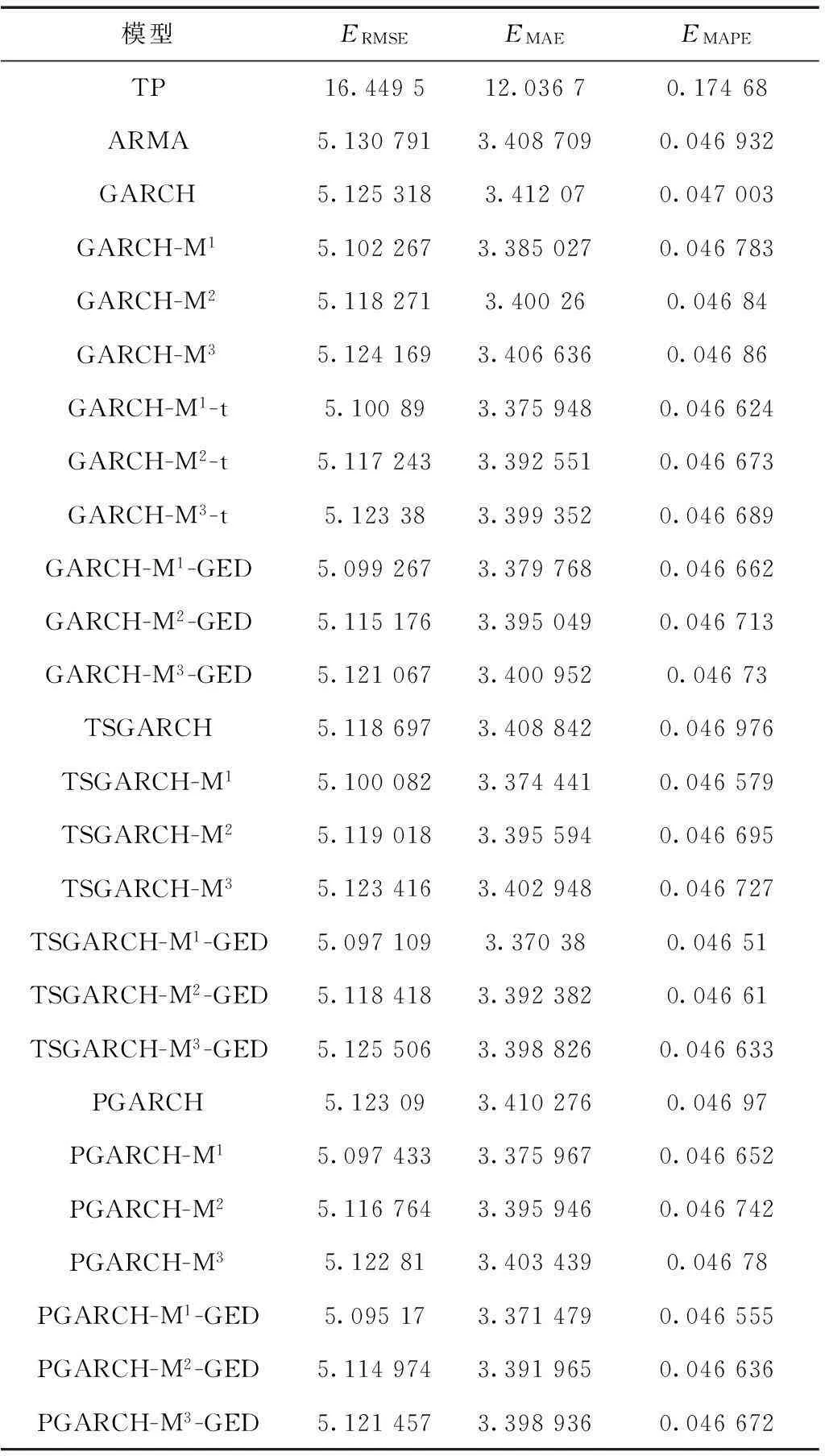
表2 短期风电功率预测结果比较
由表2预测结果比较,可得以下结论:
(1)从RMSE来看,PGARCH-M1-GED模型预测效果最好;从MAE和MAPE指标来看,TSGARCH-M1-GED模型预测效果最好。
(2)计及波动补偿项的GARCH-M族模型总体上预测效果比常规GARCH族模型预测效果更好,其中又以第一型GARCH-M族模型的预测效果为最好。本算例中波动补偿项的引入对提高预测准确度有积极意义。
(3)综合表2所列模型,计及厚尾效应的GARCH-M族模型预测效果好于常规基于正态分布的GARCH-M模型,采用厚尾分布如GED或t分布有利于预测准确度的提高。在所有考虑厚尾效应的模型中,本算例中采用厚尾分布的PGARCH-M1-GED,TSGARCH-M1-GED表现最为出色。
最后给出PGARCH-M1-GED模型的预测曲线、正负两倍标准差的预测区间及真实风电功率曲线如图6所示。
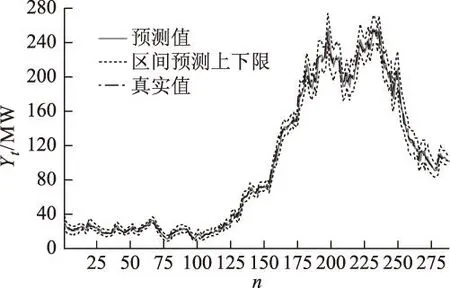
图6 基于PGARCH-M1-GED的预测曲线Fig.6 The forecasting result based on PGARCH-M1-GED
4结论
本文推广了考虑风电时间序列波动性和厚尾效应的GARCH-M类模型。基本结论如下:
1)基于GARCH-M族模型,推广了风电时间序列波动性的分析框架,借助动态波动补偿系数曲线,定量讨论了波动补偿项对风电功率预测的影响,提高了预测准确度,同时在完成风电预测的基础上进而给出了风电功率的条件方差预测值,对未来风电波动预测提供了参考。
2)基于对风电时间序列波动性结构的研究,借助动态形状参数曲线,在全样本的时间尺度内刻画了风电时间序列的厚尾效应。在讨论形状参数时变性的基础上,论证了GARCH族风电预测模型选用厚尾假设的必要性。
3)算例结果表明,以PGARCH-M1-GED和TSGARCH-M1-GED为代表的厚尾GARCH-M模型,能够刻画风电序列的厚尾效应,较好地捕捉风电时间序列的波动特征,提高了风电功率预测准确度。
参考文献
[1]李俊峰,蔡丰波,乔黎明,等.2013中国风电发展报告[R].中国资源综合利用系会可再生能源专业委员会等,2013.
[2]KLange M,Focken U.Physical approach to short term wind power prediction[M].New York:Springer-Verlag,2009.
[3]杨秀媛,肖洋,陈树勇.风电场风速和发电功率预测研究[J].中国电机工程学报,2005,25(11):1-5.
Yang Xiuyuan,Xiao Yang,Chen Shuyong.Wind speed and generated power forecasting in wind farm[J].Proceedings of the CSEE,2005,25(11):1-5.
[4]高阳,朴在林,张旭鹏,等.基于噪声场合下 ARMA模型的风力发电量预测[J].电力系统保护与控制,2010,38(20):164-167.
Gao Yang,Piao Zailin,Zhang Xupeng,et al.Prediction of wind power generation based on ARMA with additive noise model[J].Power System Protection and Control,2010,38(20):164-167.
[5]Kavasseri R G,Seetharaman K.Day-ahead wind speed forecasting using fARIMA models[J].Renewable Energy,2009,34 (5):1388-1393.
[6]Chen Hao,Wan Qiulan,Li Fangxing,et al.GARCH in mean type models for wind power forecasting[C]//IEEE Power and Energy Society General Meeting,Vancouver,BC,2013:1-5.
[7]孔波利,崔丽艳,丁钊,等.基于风光混合模型的短期功率预测方法研究[J].电力系统保护与控制,2015,43(18):62-66.
Kong Boli,Cui Liyan,Ding Zhao,et al.Short term power prediction based on hybrid wind-PV forecasting model[J].Power System Protection and Control,2015,43(18):62-66.
[8]刘荣,方鸽飞.改进 Elman 神经网络的综合气象短期负荷预测[J].电力系统保护与控制,2012,40(22):113-117.
Liu Rong,Fang Gefei.Short-term load forecasting with comprehensive weather factors based on improved Elman neural network[J].Power System Protection and Control,2012,40(22):113-117.
[9]李霄,王昕,郑益慧,等.基于改进最小二乘支持向量机和预测误差校正的短期风电负荷预测[J].电力系统保护与控制,2015,43(11):63-69.
Li Xiao,Wang Xin,Zheng Yihui,et al.Short-term wind load forecasting based on improved LSSVM and error forecasting correction[J].Power System Protection and Control,2015,43(11):63-69.
[10]孙国强,卫志农,翟玮星.基于RVM与ARMA误差校正的短期风速预测[J].电工技术学报,2012,27(8):187-193.
Sun Guoqiang,Wei Zhinong,Zhai Weixing.Short term wind speed forecasting based on RVM and ARMA error correcting[J].Transactions of China Electrotechnical Society,2012,27(8):187-193.
[11]王贺,胡志坚,张翌晖,等.基于聚类经验模态和最小二乘支持向量机的短期风速组合预测[J].电工技术学报,2014,29(4):237-245.
Wang He,Hu Zhijian,Zhang Yihui,et al.A hybrid model for short-term wind speed forecasting based on ensemble empirical mode decomposition and least squares support vector machine[J].Transactions of China Electrotechnical Society,2014,29(4):237-245.
[12]温锦斌,王昕,李立学,等.基于频域分解的短期风电负荷预测[J].电工技术学报,2014,28(5):66-72.
Wen Jinbin,Wang Xin,Li Lixue.et al.Short-term wind load forecasting based on frequency domain decomposition[J].Transactions of China Electrotechnical Society,2013,28(5):66-72.
[13]Engle R F.Autoregressive conditional heteroskedasticity with estimate of the variance of U.K.inflation[J].Econometrica,1982,50(4):987-1007.
[14]Bollerslev T.Generalized autoregressive conditional heteroskedasticity[J].Reri Research Paper,1986,31(3):307-327.
[15]Taylor S.Modeling financial time series chichester[M].UK:John Wiley and Sons,1986.
[16]Ding Z,Granger C W J,Engle R F.A long memory property of stock market returns and a new model[J].Journal of Empirical Finance,1993,1(1):83-106.
[17]Engle R F,Lilien D M,Robins R P.Estimating time varying risk premia in the term structure:the ARCH-M model[J].Econometrica,1987,55(2):391-407.
[18]陈昊.基于非高斯分布GARCH模型的负荷预测[J].电力自动化设备,2008,28(7):65-68.
Chen Hao.Load forecasting based on nongaussian GARCH model[J].Electric Power Automation Equipment,2008,28(7):65-68.
[19]Chen Hao,Wan Qiulan,Zhang Bing,et al.Short-term load forecasting based on asymmetric ARCH models[C]//IEEE Power and Energy Sciety General Meeting,Minneapolis,MN,2010:1-6.
陈昊男,1980年生,博士,教授级高工,研究方向为风电功率预测,非线性时间序列分析等。
E-mail:pingfengma@126.com(通信作者)
万秋兰女,1950年生,博士,教授,研究方向为电力系统分析与仿真。
E-mail:qlwan@seu.edu.cn
作者简介
中图分类号:TM714
收稿日期2014-09-30改稿日期2015-05-25
国家高技术研究发展计划(863计划)资助项目(2011AA05A105)。

