TSMC-S/G系统起动时的安全换流策略研究

梁　莹　周　波　刘晓宇　秦显慧　魏佳丹

(南京航空航天大学 江苏省新能源发电与电能变换重点实验室　南京　210016)



TSMC-S/G系统起动时的安全换流策略研究

梁莹周波刘晓宇秦显慧魏佳丹

(南京航空航天大学 江苏省新能源发电与电能变换重点实验室南京210016)

摘要将双级矩阵变换器(TSMC)应用于起动/发电系统以提高系统的运行可靠性。系统起动时采用id=0的矢量控制策略，TSMC单向开关侧工作于不可控整流状态。针对系统起动工作时若电机功率因数角大于30°引起的换流问题，分析了一个扇区中不同开关状态下的电流流通路径，提出了一种可行的安全换流调制策略。该调制策略选择合适的作用矢量，并合理分配作用时间，可确保系统中电流始终存在流通回路。整个系统采用电流闭环实现恒转矩起动。仿真结果和实验结果均验证了系统起动安全换流策略的可行性与有效性。

关键词：双级矩阵变换器起动/发电系统安全换流空间矢量控制起动

Research on Safe Commutation Strategy in TSMC-S/G System at Starting

LiangYingZhouBoLiuXiaoyuQinXianhuiWeiJiadan

(Jiangsu Key Laboratory of New Energy Generation and Power Conversion Nanjing University of Aeronautics and AstronauticsNanjing210016China)

AbstractThe two stage matrix converter (TSMC) is used in the starter/generator system to improve the reliability of the system.Theid=0 space vector control strategy is used at starting，and the unidirectional switch side of the TSMC is worked in the no controlled rectifier state.To solve the commutation problem caused by over 30° motor’s power factor angle，the current circulating paths with different switch states in a sector are analyzed.Then a feasible safe commutation modulation strategy is proposed，which selects appropriate vectors and allocates times reasonably，and thus ensures the existence of the current circulation loop in the system.In addition，the system uses the current closed-loop control to realize constant torque starting.The feasibility and effectiveness of the start strategy for safe commutation is validated by simulation and experimental results.

Keywords：Two stage matrix converter，starter/generator system，safe commutation，space vector control，start

0引言

起动/发电一体化技术将发动机中传统的起动机革除，减轻了重量、降低了系统成本、提高了系统可靠性，因此受到了人们的广泛关注[1，2]。功率变换器是起动/发电系统的关键部件之一，大多采用交直交型变换器，其直流侧含有储能电容，体积大，且降低了系统的可靠性。而双级矩阵变换器(Two Stage Matrix Converter，TSMC)无直流储能环节，且具有输出性能好、可实现能量双向流动以及输入功率因数高等[3-5]优点，将其应用于起动/发电系统可减小系统体积重量。

现有的研究中，大多将双级矩阵变换器双向开关侧(简称前级)作为整流级，单向开关侧(简称后级)作为逆变级。基于双级矩阵变换器的起动/发电系统(简称TSMC-S/G系统)中，以考虑发电性能为主，因此一般情况下也将电机与TSMC的前级相连。目前国内外已有很多学者将TSMC应用于风力发电系统、变速恒频发电系统等[6-8]，TSMC在发电时具有较好的性能。同时，TSMC也可用来驱动电动机以实现变频调速[9-11]，但此时电机与TSMC的后级相连，与TSMC-S/G系统起动时的拓扑不同。

目前鲜有研究将TSMC应用于起动/发电系统。文献[12]提出将矩阵整流器应用于集成起动/发电系统中，其采用可切换的输入滤波器结构，研究了系统的控制规律，分析了系统的输入输出特性。然而矩阵整流器拓扑结构与双级矩阵变换器相比，不具有逆变级，并不直接适用于交流起动/发电系统中。文献[13]将TSMC应用于交流起动/发电系统，其结构如图1所示，通过继电器Si切换起动、发电状态下的滤波器结构。起动时，继电器Si断开，不接入滤波电容Ci，电源给起动/发电机供电，后级工作于不可控整流状态。其控制策略采用三相六拍控制方式起动，优点是控制简单，不足之处是转矩脉动较大。由于TSMC没有自然的续流通道，为实现系统安全换流，文献[13]提出了两种不同的TSMC调制策略。其中，调制策略一通过后级开关管配合导通构造流通回路，后级死区时，前级采用零矢量配合，该方法适用性广，采用空间矢量调制时可借鉴此方法，但采用零矢量配合会引起较大电流畸变及转矩跌落。调制策略二仅通过控制前级开关管即可确保系统电流始终存在流通回路，该方法控制简单，易实现，但适用范围有局限性，不适用于空间矢量调制。

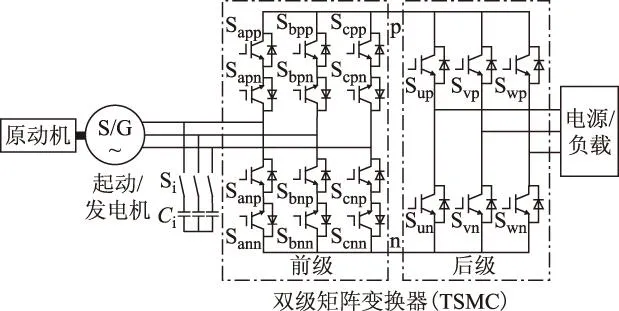
图1　TSMC-S/G系统结构图Fig.1　Topology of TSMC-S/G system

本文主要针对图1所示的TSMC-S/G系统起动时的安全换流策略进行研究。与文献[13]不同，系统采用空间矢量控制，因此其安全换流策略也不同。若电机功率因数角大于30°，会引起安全换流问题[4]，感性电流断路会产生母线电压尖峰，通过分析安全换流问题产生的原因，提出了一种TSMC的安全换流调制策略，其核心思路是选择合适的作用矢量，并合理分配作用时间，以确保系统中电流始终存在流通回路；且与文献[13]调制策略一中仅采用零矢量配合相比，能减小电流畸变和转矩跌落。仿真和实验验证了系统起动安全换流策略的可行性与有效性。

1双级矩阵变换器的基本调制策略

起动时，双级矩阵变换器的后级工作于整流状态。由于系统没有储能的大电感，且后级由单向开关构成，电源线电压最大的两相所对应的二极管会自然导通。由于起动/发电系统的起动工作时间较短，二极管不可控整流对系统的影响较小，考虑到控制的简单性，后级可采用二极管不可控整流方式。

起动时，双级矩阵变换器的前级工作于逆变状态，采用空间矢量调制策略(SVPWM)，与传统的三相逆变器工作原理一致。

前级有8种开关状态，由此可得8个基本电压空间矢量(U0～U7)。图2为各基本电压矢量的分布图，并由此划分出扇区。括号中数字对应表示a、b、c三相的开关导通状态，其中“1”表示上桥臂导通，“0”表示下桥臂导通。

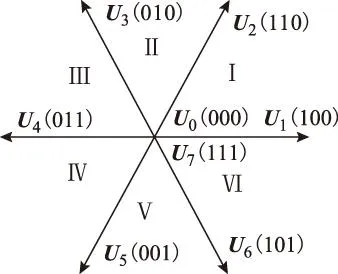
图2　电压空间矢量的扇区划分Fig.2　The sectors of the voltage space vector

当期望输出电压矢量Us落在某一扇区时，可由该扇区边界的两个非零矢量Uα和Uβ(U1～U6)与零矢量(U0，U7)合成得到，其表达式为[14]

Us=dαUα+dβUβ+d0U(0，7)

(1)

式中，dα、dβ分别为一个扇区中有效矢量Uα、Uβ对应的开关占空比；d0为零矢量对应的开关占空比。根据正弦定理，得到dα、dβ、d0的表达式分别为

(2)

式中，θo为输出相电压空间矢量Us与所在扇区起始边的角度；mv为前级逆变状态的调制系数。

(3)

式中，Uom为期望输出相电压幅值，V；Udc为直流母线电压平均值，V。

虽然前级逆变状态时工作原理与传统逆变器相同，但前级为双向开关管，可能会使换流策略复杂化。目前已有的多数研究中，TSMC前级工作于整流状态，双向开关在后级处于零矢量状态时进行换流，为零电流换流，只需要两步即可完成换流，换流较简单。而在TSMC-S/G系统中，前级工作在逆变状态，后级工作在不可控整流状态，这时后级不存在配合前级换流的零矢量，因此前级的换流需要采用传统矩阵变换器的四步换流策略，换流较复杂。

为了简化起动/发电系统中起动时TSMC的换流策略，可使双向开关中同侧的一个开关恒通，对于图1所示拓扑结构，将开关Sapn、Sbpn、Scpn、Sann、Sbnn、Scnn恒通，前级等效成普通逆变桥，系统起动时的等效电路如图3所示。此时，可采用死区换流，以简化换流过程。

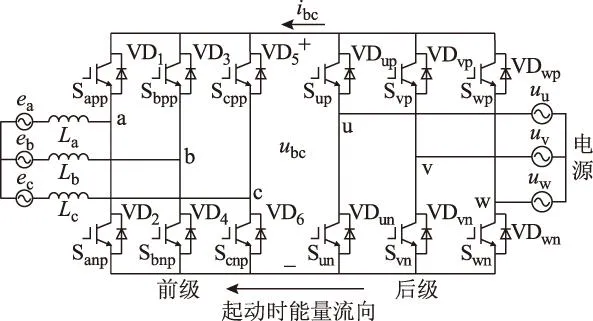
图3　系统起动等效电路Fig.3　Starting equivalent circuit of the system

2安全换流问题的分析

2.1安全换流问题的起因

在起动过程中，当电机功率因数角φ>30°时，会产生从前级流向后级的电流(idc<0)[4]，即反向电流，如果后级只采用二极管整流，由于二极管具有单向电流流动特性，电流不能反向流通。电机的感性电流断路会产生电压尖峰，只能通过钳位电路进行保护，不仅增加钳位电路的工作负担，而且需要相对地增大钳位电路中的电容值，从而削弱了TSMC的优势[15]。因此需对idc<0的情况进行分析。以扇区Ⅰ为例，由图2可知，这时前级的有效矢量为U1、U2。设电机功率因数角φ=30°+θ(θ=θ2-θ1，其中θ1为扇区Ⅰ起始处的角度，θ2为ic负向过零点的角度)，电压和电流波形如图4所示。图中ia、ib、ic为电机的电流，电流为正表示电流流入电机，从图中可知，若φ<30°，ic负向过零点在扇区Ⅵ，而当φ>30°时，ic负向过零点移至扇区Ⅰ，这时过零点与扇区Ⅰ起始处相差θ。

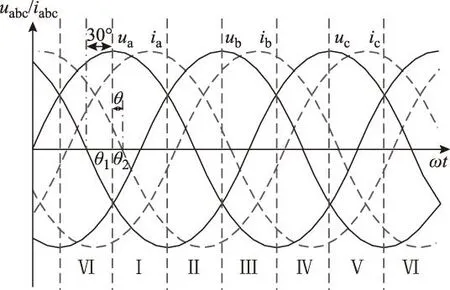
图4　各扇区电压电流示意图Fig.4　Schematic of voltage and current in each sector

对扇区Ⅰ中各矢量作用的电流状态进行分析，找出会产生反向电流的矢量。图5为扇区Ⅰ中有效矢量对应的电流状态，电流参考方向如图所示。U1(100)作用时，导通a相上桥臂和b、c相下桥臂，如图5a所示，可得直流母线电流idc=ia=-ib-ic，根据图4可看出ia在扇区Ⅰ中始终为正，即idc>0，因此U1作用不会产生反向电流；U2(110)作用时，导通a、b相上桥臂和c相下桥臂，如图5b所示，直流母线电流idc=ia+ib=-ic，要使idc>0，则要有ic<0，根据图4可看出ic在θ1～θ2角度内为正，该区间内-ic为负，即idc<0，此时出现反向电流；U0(000)作用时，a、b、c相下桥臂导通，直流母线电流idc=0，不会出现反向电流；U7(111)作用时，情况与U0类似，不会出现反向电流。

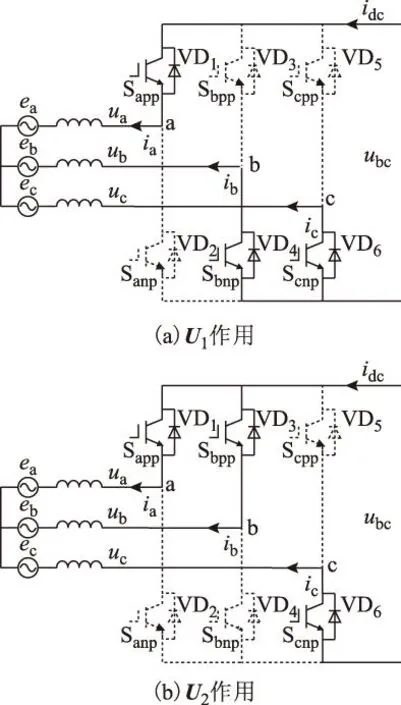
图5　扇区Ⅰ中有效矢量对应电流状态Fig.5　Current state of effective vectors in sector Ⅰ

根据上述分析，当电机功率因数角φ=30°+θ时，扇区Ⅰ中，在零矢量和U1作用下不会出现回馈至后级的反向电流，没有换流问题；而U2作用时，在扇区前端θ角度内(θ1～θ2)将出现反向电流，由于二极管的电流单向流动特性致使电流没有回路，出现换流问题。

依此可得当φ>30°时各扇区中会引起换流问题的矢量，分别为每个扇区中的Uβ，如表1所示。

表1　φ>30°时各扇区中会引起换流问题的矢量

2.2参数对安全换流问题的影响

本节具体分析在什么状态下会出现电机功率因数角大于30°的情况。

基于双级矩阵变换器的起动/发电系统在起动时采用id=0的空间矢量控制，通过PI调节器控制电流跟随给定实现恒转矩起动。

此时的转矩可简化为

Te=1.5np(ψpm+Mfif)iq

(4)

式中，Te为电磁转矩，N·m；np为电机极对数；iq为定子交轴电流，A；if为励磁绕组电流，A；ψpm为永磁体匝链的磁链，Wb；Mf为电枢绕组与励磁绕组的互感，H。永磁电机中Mf为0，励磁电机中ψpm为0。由此，可控制励磁电流恒定，则电磁转矩正比于q轴电流，控制q轴电流幅值就能较好地控制转矩。

根据以上控制方法，电流方向为q轴方向，功率因数角φ即为期望输出矢量与q轴之间的夹角，可表示为

(5)

式中，Rs为定子电阻，Ω；ωe为电角速度，rad/s；p为微分算子。

假设在起动过程中，励磁电流if和q轴电流iq均控制为恒定值，则式(5)可简化为

(6)

随着转速n升高，φ变大，定子电阻上的电压很小，可忽略不计，此时转速变化对φ的影响不大，因此式(6)在高速时可简化为

(7)

根据式(7)可知，当励磁电流if增大时，功率因数角φ减小；当给定q轴电流iq增大时，功率因数角φ增大。

一般系统采用2～3倍额定电流起动，起动时采用额定励磁电流。而起动电流越大，iq越大，功率因数角越大，就越容易出现回馈至后级的反向电流，而增大励磁电流对功率因数角的影响有限，因此需采用能实现安全换流的调制策略。

3双级矩阵变换器的安全换流调制策略

3.1后级调制策略

为了给回馈至后级的反向电流构建流通通路，可将后级导通二极管的反并联开关管配合导通。

将输入相电压矢量划分扇区，如图6所示。以扇区3为例，此时uv>uu>uw，图3中二极管VDvp、VDwn导通，则对应Svp、Swn导通，依此可得后级各扇区的开关状态，如表2所示。

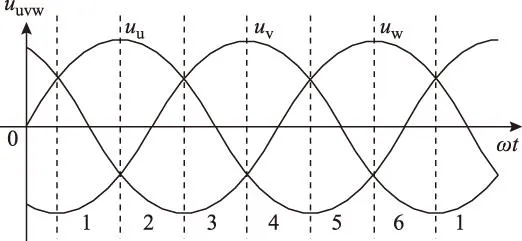
图6　双级矩阵变换器后级电压扇区划分Fig.6　The voltage sectors of the last stage

扇区123456导通SupSupSvpSvpSwpSwp开关SvnSwnSwnSunSunSvn

需要注意的是，开关管必须与其反并联二极管的导通状态保持一致，不能提前导通或滞后关断，否则会引起电源短路。因此，在换相时，开关管需要加入死区，死区可保证二极管换相点处没有开关管误导通，从而防止电源短路而产生过电流[13]。图7为死区示意图，死区时间为t1～t2，先关断需要关断的开关管，再导通需要开通的开关管，二极管自然换相需确保在死区内完成。

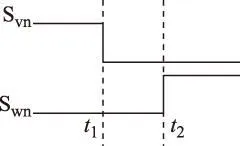
图7　后级第1扇区切换至第2扇区Fig.7　The last stage switching from first sector to second

3.2前级调制策略

在后级非死区期间，前级采用常规的SVPWM调制即可；而在后级死区期间，如果前级有回馈至后级的电流，后级就没有了流通回路，此时需要前级能自行续流。最简单的方法就是导通前级全部上桥臂或下桥臂的开关管(即作用零矢量)[13]，此时idc=0，前级不会产生回馈至后级的电流。

由于数字控制检测延时等原因，死区时间需要较大的裕量，零矢量的较长时间插入会使电流跌落，从而引起转矩跌落，影响起动性能。根据2.1节分析可知，后级死区时，每个扇区只能作用Uα和零矢量，且需要合理地分配有效矢量Uα的作用时间。由于Uα与期望矢量Us存在一定夹角，若Uα作用时间过长，会使转矩突增；若Uα作用时间过短，会使转矩突降。因此，选择合适的Uα作用时间可尽量减少转矩的变化。

对应式(2)中非死区时的各矢量占空比，死区时，Uβ不作用，Uα的长度可选择为期望矢量长度乘以补偿系数kd，则当后级死区时，各矢量占空比为

(8)

由于后级死区期间前级作用的矢量发生变化，零矢量的排列和选择也会有所改变。无死区时，采用的矢量分布方法为“五段式”分布，即在扇区Ⅰ中矢量作用顺序为U1→U2→U7→U2→U1。而死区时U2不作用，若不改变其他矢量排列，则矢量作用顺序为U1→U7→U1。由于开关变换时应尽可能选择开关切换次数少的零矢量以减少开关损耗，而U1(100)变换到U7(111)时需要切换2个开关，因此可将中间零矢量修改为U0(000)，即矢量作用顺序变为U1→U0→U1。依此可得其他各扇区在死区时的矢量作用情况，如表3所示。

表3　后级死区时各扇区作用矢量

因此，φ>30°时，前级需要在后级死区时采用本文所提策略配合，而当起动性能要求不高或为了减小控制复杂度时，后级开关管可不导通。这时相当于后级一直处于死区期间，而前级则全部采用后级死区时的策略，这种策略的优点是控制简单，但由于前级一个扇区仅作用一个有效矢量，转矩脉动会增大。

3.3小结

总结上述分析结果，起动时电机的功率因数角φ不同，可采取不同的调制策略：①若φ<30°，不存在前级流向后级的电流，后级开关管无需导通，前级采用常规的SVPWM调制，即第一节中的TSMC基本调制策略；②若φ>30°，后级开关管配合导通，后级死区时，前级采用本文所提策略配合，构造流通回路，并减小转矩跌落；③若φ>30°，且当起动性能要求不高或为了减小控制复杂度时，后级开关管不导通，前级全部采用后级死区时的策略配合。

该安全换流策略也可为其他可能出现功率因数角超过30°以及能量回馈等情况提供解决思路。

4仿真与实验验证

4.1仿真研究

为了验证上述分析的可行性，利用Matlab搭建仿真模型，对系统进行起动仿真。仿真参数为：输入电源相电压有效值50 V，频率50 Hz；开关频率10 kHz；4对极的同步电机，电机相电感2.2 mH，电阻0.7 Ω；起动时要达到转速500 r/min；起动电流幅值13 A，此时电机功率因数角未超过30°。

起动过程并不需要转速环控制，但为了限制转速进一步升高，仿真和实验中均加入转速环，转速环的加入并不会对起动过程产生影响。转速波形如图8所示，可见系统能平稳实现所需转速。

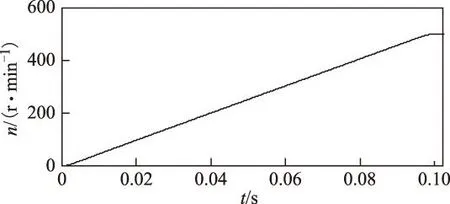
图8　转速波形Fig.8　Simulation waveform of speed

比较不同调制策略下的转矩波形，如图9所示，由式(4)可知转矩正比于iq，因此同时给出iq波形，以说明iq可反映转矩。由于电机功率因数角φ<30°，后级开关管无需导通，前级直接采用SVPWM调制，系统有较好的起动性能，如图9a所示。虽然此时后级开关无需导通，但为了将本文所提策略的性能与其进行对比，后级加入死区，图9b、图9c分别为后级死区时采用零矢量和采用本文所提策略配合的波形。将其与图9a进行对比，可见若后级死区时前级仅采用零矢量配合会产生较大转矩跌落，而采用本文所提策略配合能减少转矩跌落，且与图9a相比，转矩跌落并不大。

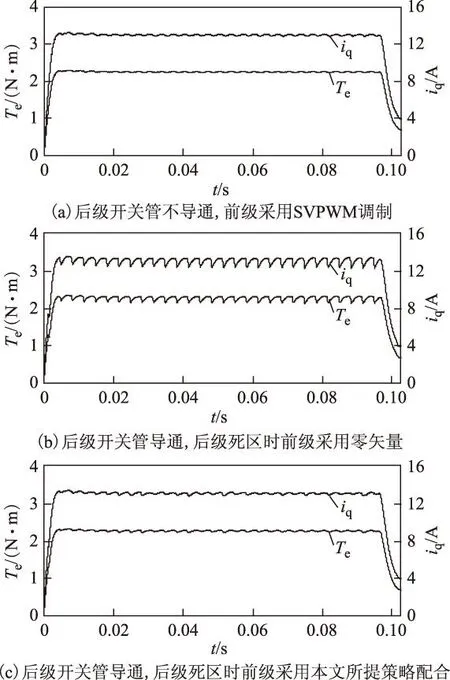
图9　φ<30°不同调制下的转矩和q轴电流波形Fig.9　Simulation waveforms of torque and q-axis current under different modulation strategies at φ<30°

为了验证电机功率因数角超过30°的情况，根据式(7)，增大电机电感和电流以提高φ，增大电机电感2 mH，起动电流幅值提高到18 A。

若后级开关管不导通，随着转速上升，φ逐渐增大，φ>30°时，母线上会出现电压尖峰，如图10a所示。电压尖峰的产生是由于回馈至后级的电流从钳位电路流过，而钳位电路将电压尖峰控制在可接受的范围内。当后级开关管配合导通，但后级死区时前级不采用本文所提策略配合，那么在后级死区期间出现的反向电流就会产生直流母线电压尖峰，如图10b所示。而后级死区期间采用本文所提策略配合后，前级构造出流通回路，电流母线电压不会产生尖峰，如图10c所示。

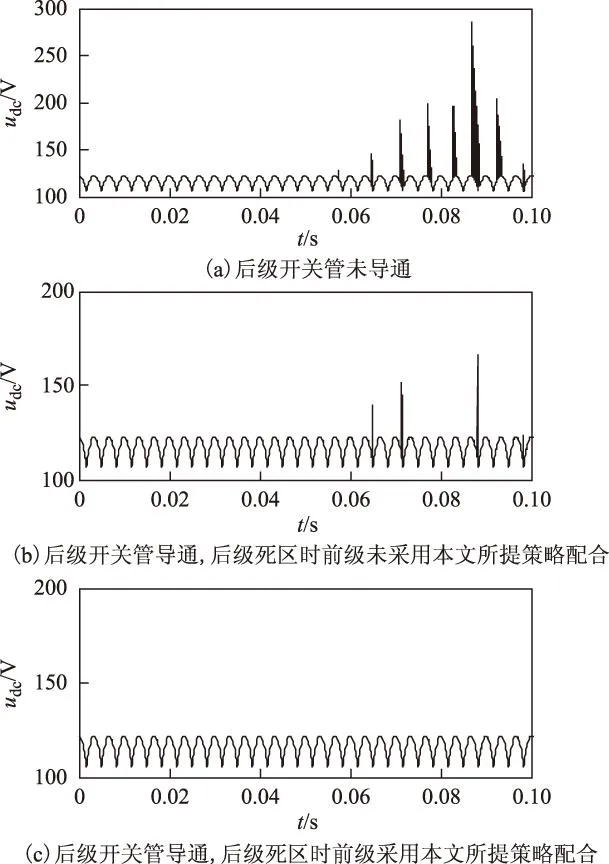
图10　φ>30°的直流母线电压波形Fig.10　Simulation waveforms of DC-bus voltage at φ>30°

4.2实验验证

系统实验平台以TMS320LF2812为控制系统核心，以18个IGBT为主功率器件(双向开关采用共射极方式相连)，以一台2 kW、4对极同步电机为样机，电机相电感2.2 mH，电阻0.7 Ω。实验参数为：输入电源相电压有效值50 V，频率50 Hz；开关频率10 kHz；电机起动转速500 r/min；起动电流幅值13 A。

图11为给定500 r/min时整个起动过程的实验波形，系统能实现恒转矩起动。由于实验机组的转动惯量较大，且负载较大，因此电机的转速上升较慢，起动时间较长。

目前实验室的机组均为小功率电机，没有功率因数角超过30°的情况，而在实际系统中起动/发电机的功率较大，更易出现该现象。因此根据现有样机参数情况，不采用安全换流策略也不会存在换流问题。图12为不同调制策略在400 r/min下的q轴电流和电枢电流波形。当后级开关管不导通，前级直接采用SVPWM调制时，波形如图12a所示，通过观测iq得到转矩情况，由图可见系统具有较好的起动性能。虽然此时后级开关无需导通，但为了验证本文所提调制策略的性能，起动时后级加入死区，并进行对比。由图12b可知，后级死区时，前级仅采用零矢量会有较大转矩脉动和明显电流畸变，与图12a没有死区时相比，死区影响很大；而采用本文所提策略配合能大大减小转矩脉动和电流畸变，如图12c所示，且与没有死区时相比，死区带来的影响并不大，体现了本文所提策略的优势。图13为输入三相电源电压及对应计算出的死区信号。

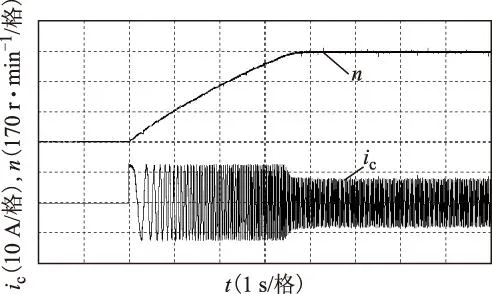
图11　给定500 r/min时起动波形Fig.11　Starting waveforms at 500 r/min

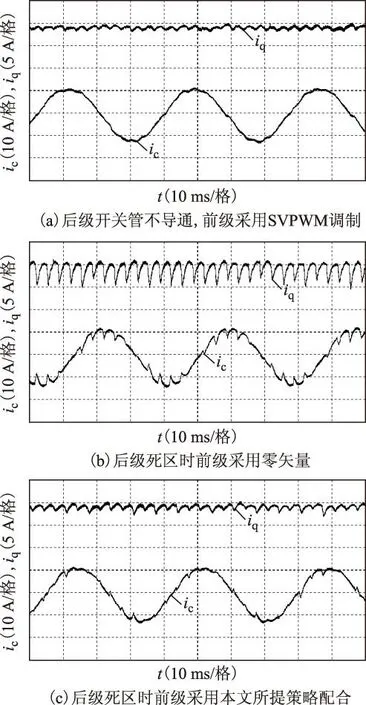
图12　400 r/min下不同调制策略的q轴电流及电枢电流波形Fig.12　Waveforms of q-axis current and armature current under different modulation strategies at 400 r/min

图13　输入电源电压与死区信号Fig.13　Input AC source voltage and dead-time signal

由于受机组条件限制，为了验证本文的分析以及所提策略的作用，实验中通过改变电机参数(串联了2 mH电感，并提高起动电流幅值至18 A)来实现功率因数角超过30°的情况。此时若不导通后级开关管，前级未采用配合策略而仅采用常规的SVPWM，直流母线电压在扇区开始时会存在尖峰，如图14a所示；由于在后级死区产生电压尖峰的概率较小，难以捕捉，易知后级配合导通能构造流通回路[4]，因此为了验证本文所提安全换流策略能构造流通回路，前级全部采用后级死区时的配合策略进行起动，在同一转速下，母线电压始终没有尖峰，如图14b所示，此时由于前级一个扇区仅一个有效矢量作用，电流正弦度下降，起动性能变差。

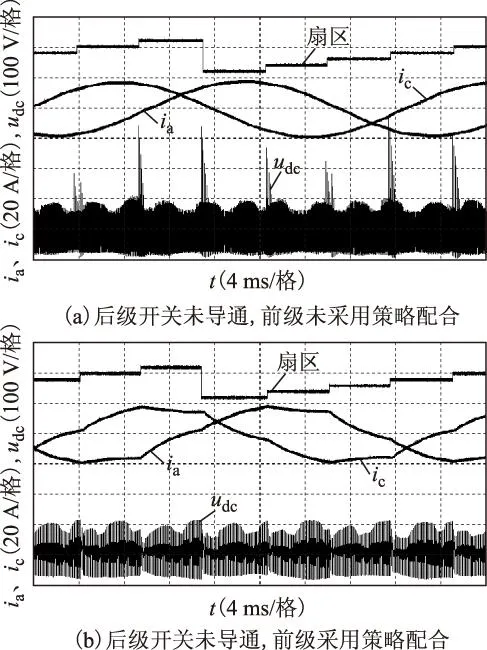
图14　φ>30°时的起动波形Fig.14　Starting waveforms when φ>30°

5结论

本文提出一种适用于TSMC-S/G系统起动的安全换流策略，通过理论分析、仿真和实验验证，得到以下结论：

1)分析了换流问题产生的原因，且分析了影响功率因数角φ的相关电机参数。当n、iq越大，φ越大，就越容易出现回馈至后级的电流，此时需要采用本文所提出的策略。

2)针对当φ>30°，TSMC没有自然续流通道的问题，提出合适的调制策略，通过其前后级相互配合，构造流通回路，以避免钳位电路吸收电压尖峰带来的损耗及成本增大等问题，同时尽可能减少转矩跌落。

参考文献

[1]Schofield N，Long S.Generator operation of a switched reluctance starter/generator at extended speeds[J].IEEE Transactions on Vehicular Technology，2009，58(1)：48-56.

[2]Griffo A，Drury D，Sawata T，et al.Sensorless starting of a wound-field synchronous starter/generator for aerospace applications[J].IEEE Transactions on Industrial Electronics，2012，59(9)：3579-3587.

[3]齐琛，陈希有.一种可靠换流的双级矩阵变换器载波调制策略[J].电工技术学报，2013，28(6)：184-191.

Qi Chen，Chen Xiyou.A carrier-based modulation strategy of two stage matrix converter with reliable commutation[J].Transactions of China Electrotechnical Society，2013，28(6)：184-191.

[4]Kolar J W，Friedli T，Rodriguez J，et al.Review of three-phase PWM AC-AC converter topologies[J].IEEE Transactions on Industrial Electronics，2011，58(11)：4988-5006.

[5]肖鲲，王莉娜，裴晓宇.多电飞机中双级矩阵变换器的改进控制方法[J].电工技术学报，2011，26(S1)：8-14.

Xiao Kun，Wang Lina，Pei Xiaoyu.Research on modulation strategy for two-stage matrix converter in more electric aircraft[J].Transactions of China Electrotechnical Society，2011，26(S1)：8-14.

[6]Pena R，Cardenas R，Reyes E，et al.Control of a doubly fed induction generator via an indirect matrix converter with changing DC voltage[J].IEEE Transactions on Industrial Electronics，2011，58(10)：4664-4674.

[7]Xiong L，Poh C L，Peng W，et al.Distributed generation using indirect matrix converter in reverse power mode[J].IEEE Transactions on Power Electronics，2013，28(3)：1072-1082.

[8]林崎，毕睿华，李先允，等.双级矩阵变换器在统一潮流控制器中的应用研究[J].电力系统保护与控制，2011，39(9)：65-71,76.

Lin Qi，Bi Ruihua，Li Xianyun，et al.Study of the application of matrix converter in unified power flow controller[J].Power System Protection and Control，2011，39(9)：65-71,76.

[9]Yang M，Gang L，Kai S.High performance vector control of IPMSM drive fed by indirect matrix converter[C]//Applied Power Electronics Conference and Exposition，Fort Worth，TX，2011：1642-1647.

[10]Ejlali A，Khaburi D A，Behnia H.DTFC based indirect matrix converter using active flux concept for IPMSM drive[C]//Proceedings of 2011 46th International Universities’ Power Engineering Conference，Soest，Germany，2011：1-4.

[11]Faraji V，Khaburi D A.A new approach to DTC-ISVM for induction motor drive system fed by indirect matrix converter[C]//Power Electronics，Drive Systems and Technologies Conference，Tehran，2011：367-372.

[12]Keping You，Rahman M F.A matrix-Z-source converter with AC-AC bidirectional power flow for an integrated starter alternator system[J].IEEE Transactions on Industry Applications，2009，45(1)：239-248.

[13]刘晓宇，周波，梁莹，等.TSMC-S/G系统起动时TSMC的调制策略[J].电工技术学报，2014，29(3)：260-269.

Liu Xiaoyu，Zhou Bo，Liang Ying，et al.Research on starting modulation strategy of TSMC in TSMC-S/G system[J].Transactions of China Electrotechnical Society，2014，29(3)：260-269.

[14]阮毅，陈伯时.电力拖动自动控制系统——运动控制系统[M].北京：机械工业出版社，2009：134-141.

[15]孙凯，周大宁，梅杨.矩阵式变换器技术及其应用[M].北京：机械工业出版社，2007：121-126.

梁莹女，1989生，硕士研究生，研究方向为功率变换技术。

E-mail：609971152@qq.com(通信作者)

周波男，1961生，教授，博士生导师，研究方向为新能源发电技术、航空电源系统、电机及其控制与功率变换技术。

E-mail：zhoubo@nuaa.edu.cn

作者简介

中图分类号：TM46

收稿日期2015-01-09改稿日期2015-12-10

国家自然科学基金(51177069)和江苏省高校优秀科技创新团队资助项目。