拓宽双级式矩阵变换器反向发电功率范围的控制策略

卞金梁　周　波　雷家兴　秦显慧　梁　莹

(南京航空航天大学　江苏省新能源发电与电能变换重点实验室　南京　210016)



拓宽双级式矩阵变换器反向发电功率范围的控制策略

卞金梁周波雷家兴秦显慧梁莹

(南京航空航天大学江苏省新能源发电与电能变换重点实验室南京210016)

摘要基于一种双级式矩阵变换器反向发电系统结构，研究其实现升压发电的控制方法，提出一种能够拓宽反向发电功率范围的控制策略，对变换器调制比进行闭环控制，使得轻载时发电机能自动减小励磁电流，从而使系统能够正常工作。这种励磁调节的方法与常规的恒压励磁控制不同，它是将励磁控制与变换器调制比控制相结合，拓宽了反向发电功率范围，提高了系统性能。实验结果验证了该新型控制策略的有效性。

关键词：双级式矩阵变换器升压发电励磁控制拓宽反向发电功率范围

Control Strategy for Broadening the Reverse Power Generation Range of Two Stage Matrix Converters

BianJinliangZhouBoLeiJiaxingQinXianhuiLiangYing

(Jiangsu Key Laboratory of New Energy Generation and Power Conversion Nanjing University of Aeronautics and AstronauticsNanjing210016China)

AbstractThe control strategy of realizing boost generation under a structure of two stage matrix converter (TSMC) reverse power generation is investigated.A new control strategy which can broaden the reverse power generation range is proposed.The closed loop control is set up for the modulation ratio in order to decrease the exciting current automatically with light load so that the system can be under control.Different from the conventional constant voltage excitation control，this method combines the excitation control with the modulation ratio control，and thus broadens the reverse power generation range and improves the performance of the system.The feasibility of the new control strategy is verified through the experimental results.

Keywords：Two stage matrix converter (TSMC)，boost generation，excitation control，broaden reverse power generation range

0引言

分布式发电以其独特的优势适应了分散的电力需求与资源分布，是大电网有益的辅助和重要补充，提高了电网的可靠性[1，2]。功率变换器是分布式发电系统的关键组成部分之一。传统的交流发电系统多采用交-直-交变换器，它们技术成熟、应用广泛，然而其直流母线大容量电解电容的存在增加了系统的体积和重量，降低了可靠性[3]。双级式矩阵变换器(Two Stage Matrix Converter，TSMC)是一种无需直流母线储能元件、易实现单位功率因数的交交变换器，具有较大的发展潜力和应用前景[4-6]。将双级式矩阵变换器应用于分布式发电系统可发挥双级式矩阵变换器结构上的优势，减小系统的体积和重量。

图1为两种双级式矩阵变换器发电系统结构，双级式矩阵变换器由两部分构成：①电流型变换器(Current Source Converter，CSC)，由6个双向开关构成，每个双向开关可采用2个IGBT共射级结构；②电压型变换器(Voltage Source Converter，VSC)，由6个单向开关构成。

图1　两种双级式矩阵变换器发电系统结构Fig.1　Two structures of TSMC generation system

传统的发电系统结构如图1a所示，发电机通过滤波电容与CSC连接，RL负载与VSC连接。这种发电结构为降压型变换器，不适合分布式发电系统电压较低的场合。文献[7]的发电系统结构与图1a相似，采用了发电机恒端电压闭环控制和变换器输出电压瞬时值闭环控制策略。文献[8]研究了图1b的反向发电结构，用电源与电感串联模拟发电机，这种发电结构的优点是能够实现升压发电，适用于分布式发电系统发电机端电压较低的场合，同时滤波器设计难度降低，该文对发电系统接负载和并网运行这两种工况进行了研究[9，10]。

本文对反向发电结构的控制策略进行了研究，分析了现有控制策略下系统实现正常发电运行的负载功率范围，发现图1b发电系统在负载较轻时，负载电压和发电机电流会失去控制，系统不能正常工作。此时需要调节发电机励磁，但采用文献[7]所述恒端电压励磁调节方法也不可行。针对此问题，提出一种能够拓宽发电功率范围的新型控制策略，在负载电压幅值闭环和发电机电流dq轴闭环基础上，对变换器的调制比和励磁电流进行闭环控制。这种励磁调节的方法将励磁控制和变换器调制比闭环控制相结合，在轻载时自动减小励磁电流，降低反电动势，从而使系统能够正常工作，有效拓宽了发电功率范围，提高了系统性能。还搭建了实验平台，通过实验对比了现有控制策略和新型控制策略，实验结果验证了该新型控制策略的有效性。

1双级式矩阵变换器反向发电系统基本原理

双级式矩阵变换器反向发电结构和传统发电结构功率流动的方向相反，其正向和反向功率流动特性是由其拓扑结构本身决定的，通过控制策略在CSC和VSC之间交换功率时，拓扑结构提供了自然的功率流通路径，与调制策略无关，因此本文发电结构的调制策略与传统发电结构调制策略相同，均为空间矢量调制算法[11-16]，它包括CSC的电流空间矢量调制算法和VSC的电压空间矢量调制算法以及两级的协同控制策略。

根据双向开关级调制信号可得到电流矢量I1，进而可判断扇区，并选择最近的两个非零矢量Im和In合成I1，设Im和In的占空比分别为dm和dn，计算公式分别为

(1)

式中，θc为I1的扇区角。

根据VSC的调制信号可得到电压矢量U1，U1同样可以由最近的两个非零矢量Ur和Us合成，设Ur和Us的占空比分别为dr和ds，计算公式分别为

(2)

式中，m为变换器的调制比；θv为U1的扇区角。

双级式矩阵变换器直流母线环节无大容量储能电容，CSC和VSC存在耦合，需要协同控制，如图2所示。定义对输入电流和输出电压空间矢量均无贡献的矢量为通用零矢量[12]，通用零矢量占空比d0的计算公式为

d0=1-(dm+dn)(dr+ds)

(3)

将通用零矢量分配在一个开关周期的开始和结尾，这样CSC可在直流母线电流为零时进行开关切换，实现零电流换流。

图2　一个开关周期内矢量分配Fig.2　Vector distribution of one switching cycle

双级式矩阵变换器CSC采用零电流换流，若不考虑VSC的死区时间，且保证变换器工作在线性调制区域时，m最大值可取1。但在实际情况中，由于功率器件的非理想特性，每段零矢量的作用时间不能小于死区时间，因此m的最大值要小于1。本文实验中，VSC死区时间为1.5 μs，占开关周期时间的1.5%，则所有零矢量作用时间比重不小于12%，即实际的m最大值为0.88。考虑到系统的动态性能以及变换器的利用率，系统额定工作状态下m的取值一般稍小于最大值，本文中取0.85。

文献[17]指出，传统调制方法下，双级式矩阵变换器CSC功率因数角需要限制在(-π/6，π/6)范围内，否则直流母线电压将为负值，引发VSC桥臂直通等危险。在图1b所示结构中，在负载较轻时，CSC功率因数较低，会超出上述范围，因此本文采用文献[18]提出的方法，通过重新组合CSC和VSC的开关状态，始终保证直流母线电压为正值，从而将CSC功率因数角范围拓宽到[-π/2，π/2]。

2现有控制策略和负载功率范围

2.1恒定励磁控制策略

图3　恒定励磁控制策略框图Fig.3　Diagram of constant excitation control strategy

2.2恒端电压控制策略

2.1节所述的恒定励磁控制策略忽略了发电机的电枢反应对电机端电压的影响。当发电机的电枢电感较大时，电机端电压幅值的波动较大。因而，文献[10]采用了恒端电压控制策略，如图4所示。虽然它针对图1a所示发电系统，但也适用于本文研究的图1b系统。这种控制方法在图4所示方法的基础上增加了发电机端电压和励磁电流闭环控制，与恒定励磁控制不同，恒端电压控制能减小电机电枢反应对励磁电流的影响，进而减小端电压波动对输出电压性能的影响。电压外环控制使得发电机端电压能够跟随给定值，励磁电流内环控制可减小励磁电压波动对励磁电流的影响。

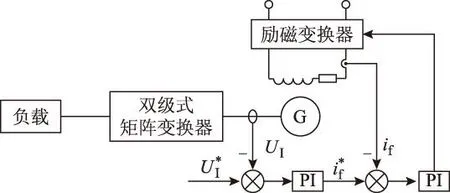
图4　恒端电压控制策略框图Fig.4　Diagram of constant terminal voltage control strategy

2.3负载功率范围

在上述两种控制方式下，发电机端电压均可当作恒定值，这也是现有控制策略下反向发电系统轻载时不能正常工作的重要原因。下面对现有控制策略下负载功率范围进行详细分析。

双级式矩阵变换器具有如下电压约束关系

(4)

式中，UI为发电机端电压有效值，V；UR为滤波电容Cf两端电压有效值，V；φR为CSC的功率因数角。cosφR可根据负载侧电路得到

(5)

式中

A=1-2ω2LfCf

(6)

(7)

式中，ω为输出电压的角频率，rad/s；P为负载功率，W；Uo为负载电压有效值，V；Lf为滤波电感参数，mH；Cf为滤波电容参数，μF。

根据式(5)可得功率因数角φR与负载功率P的关系曲线，如图5所示。由图可知，当负载功率P较小时，φR较大，则负载侧功率因数cosφR较小。由式(3)和上文的分析可知，尽管UI与m和cosφR有关，但在变换器工作于线性调制区域时，m的取值已接近其理论最大值，故m的调节范围较小，当负载功率因数较小时，若要避免UI减小，即使增大m也效果甚微。当负载功率较小时，取极限情况(空载)，假设系统能正常工作并达到稳态，此时cosφR=0，由式(4)可知UI=0，现有控制策略下Ugs恒定，对式(9)求解，发现电流Is无解。然而实际发电机电枢绕组中会流过电流，负载电压会被迫抬升，实际负载电压会大于给定值，则实际负载功率会大于期望功率，实际发电机电流会大于期望值。此时系统不能正常工作，发电机电流和负载电压会失去控制。下面分析现有控制策略下系统正常工作时的最小负载功率。

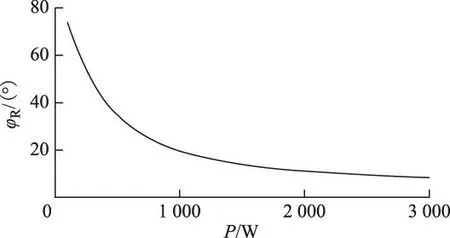
图5　功率因数角与负载功率的关系Fig.5　Relationship between power factor angle and load power

根据负载侧电路，滤波电容Cf两端电压有效值UR与负载电压Uo关系为

(8)

发电机侧，控制发电机反电动势ugs和发电机电流is同相位，可得UI的另一个表达式为

(9)

式中，Ugs为发电机反电动势有效值，V；Is为发电机电枢电流有效值，A；Ls为电枢电感值，mH；Rs为电枢电感电阻，Ω；ωs为电枢电流的角频率，rad/s。

由式(4)、式(8)和式(9)可得负载功率P与变换器调制比m的约束关系。将表1所示系统参数代入，可得到不同发电机反电动势下系统负载功率P与调制比m的关系曲线，如图6所示。由图可知：

1)发电机反电动势一定时，在曲线的上半段，随着P的增大，m也随之增大，在曲线的下半段，随着P的增大，m随之减小，当m取最大值(本文中为0.88)时，对应系统能正常工作的最小功率。

2)发电机反电动势越小，系统正常工作时的最小功率就越小，然而额定工作状态时变换器的电压利用率较小，而且相同功率条件下发电机的电枢电流较大，不利于发电机正常运行。

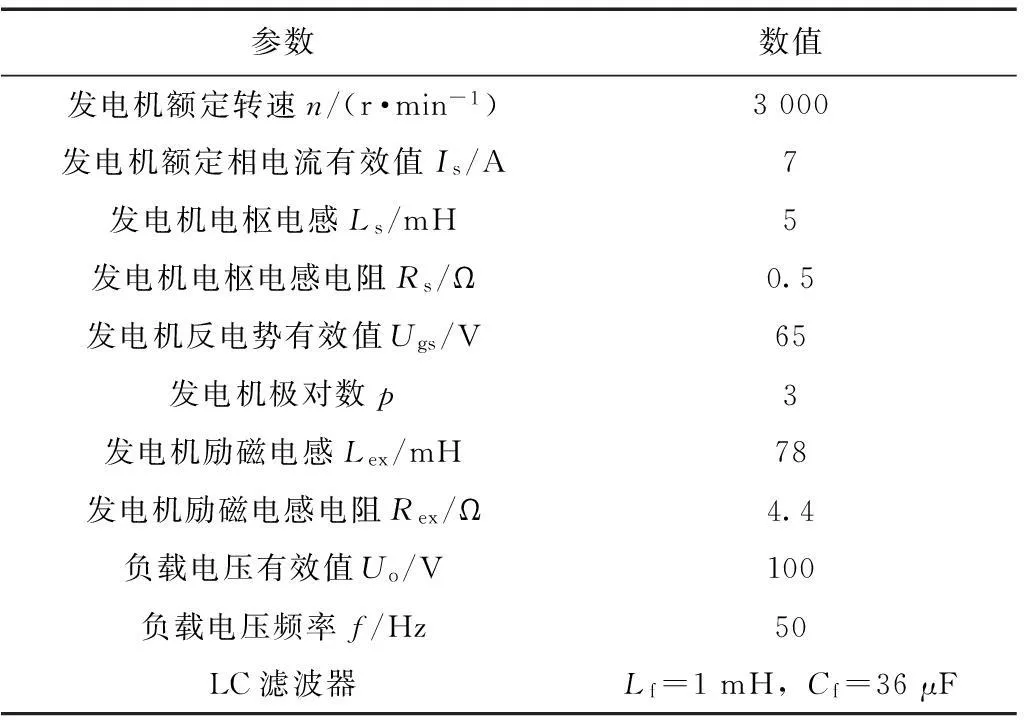
表1　系统参数

图6　不同反电动势下系统负载功率与调制比的关系Fig.6　Relationship between power and modulation ratio under different back EMF

m取最大值0.88时，对应系统正常工作时的最小功率，Pmin=653 W。当发电功率小于Pmin时，系统将不满足式(4)的约束关系，发电机电流和负载电压波形会畸变。所以在现有控制策略下，系统正常工作时的最小功率为653 W。

3拓宽发电功率范围的控制策略

根据上面的分析，负载较轻时，负载侧功率因数较低，由于在现有控制策略下发电机的励磁调节与变换器控制是各自孤立的，系统不能正常工作。此时，可将变换器控制和励磁调节相结合，在系统轻载时，根据负载大小自动减小发电机反电动势，使发电机电流和负载电压可控。

本文提出一种控制策略，如图7所示，在图3所示控制策略基础上，增加变换器调制比闭环控制和发电机励磁电流闭环控制，将励磁调节和变换器控制相结合，调制比闭环控制使变换器调制比保持恒定状态，实际调制比m能跟随给定值m*。励磁电流闭环控制使得系统在负载较轻时，根据调制比外环产生的信号自动减小励磁电流，进而减小发电机反电动势，使得发电机电流可控，负载电压能够跟随给定值，从而使系统能够正常工作。

图7　拓宽发电功率范围的控制策略Fig.7　Control strategy of broadening power range

该新型控制策略下，发电系统的理论负载功率范围为空载至额定负载。但在实际系统中，当负载很轻时，根据前文的分析，则发电机反电动势很小，即需要发电机励磁电流很小，变换器在初始建压时刻需要一定的有功电流，发电机的电枢反应会对励磁磁动势造成较大影响，使得气隙磁场畸变严重，且电枢电流一定时，励磁电流越小，电枢反应对其的影响越大。在本文所述系统中，由于额定工作状态下发电机的励磁电流和反电动势均较小，为了保证系统性能和控制准确度，假定轻载时发电机的励磁电流和反电动势调节不能小于额定时的50%(若进一步减小，则电枢反应对励磁磁动势的影响更大，控制性能会变差)。由 式(4)、式(8)和式(9)的电压约束关系可计算出系统正常工作时的最小功率为200 W。若继续减小负载功率，则励磁电流将过小，电枢反应对气隙磁场的影响较大，造成气隙磁场不稳，发电机输出性能变差，同时系统控制准确度也会变差，引起系统崩溃。

本文所提新型控制策略下，发电功率范围由现有控制策略下额定值的50%～100%拓宽至15%～100%。

若忽略发电机电枢电感和内阻以及滤波电感压降，则UI近似与发电机反电动势Ugs相等，UR近似与负载电压Uo相等，发电机端电压有效值UI为[7]

UI=K1if

(10)

式中，K1为发电机输出电压与励磁电流之间的折合系数。由式(4)可得m和UI之间的关系为

m=K2UI

(11)

式中

(12)

根据以上关系式可得到系统闭环控制结构框图，如图8所示。外环为调制比闭环，内环为励磁电流环。Gm(s)、Gf(s)分别为调制比外环和励磁电流内环的PI调节器。其中

(13)

(14)

式中，Kmp和Kfp分别为调节器比例环节系数；Kmi和Kfi分别为调节器积分环节系数。系统闭环传递函数为

(15)

式中

(16)

将各参数代入式(16)，得到图9所示的幅频和相频曲线。

图8　系统闭环控制结构框图Fig.8　Diagram of closed loop control

图9　闭环控制系统波特图Fig.9　Bode figure of closed loop control

从图9中可看出，低频时输出可较好地跟踪给定值，系统具有较高的稳定裕度；由于发电机励磁电感较大，励磁调节动态响应较慢，然而系统的动态性能除了由励磁控制决定之外，还由发电机电枢电流闭环控制决定。

m*的选取既不能过小，也不能过大。若m*过小，则非零矢量作用时间很短，系统稳定性和输出波形质量会变差；若m*过大，则系统过调制同样导致输出波形质量变差。为了使系统处于线性调制区域，考虑到VSC开关管死区时间，m*取0.85。这样既保证了变换器的电压利用率，同时使得变换器工作在线性调制区域。

4实验验证

4.1实验平台

为验证本文提出的拓宽发电时负载功率范围控制策略的有效性和可行性，采用一套由永磁同步电动机和电励磁同步发电机以及双级式矩阵变换器构成的机组进行实验验证。实验中采用永磁同步电动机作为原动机，极对数为4，额定转速为3 000 r/min。电励磁同步发电机参数如表1所示。

双级式矩阵变换器CSC采用两个600 V/50 A的双向开关模块APTGT50TDU60PG，每个模块含有3个双向开关，每个双向开关由2个IGBT共发射极连接，VSC由600 V/75 A的IPM模块PM75RLA060构成。控制器采用TI公司的DSP(TMS320F28335)与Altera公司的CPLD(EPM1270)，CSC开关频率为10 kHz，VSC开关频率为20 kHz。实验中，发电机转速3 000 r/min，负载电阻23 Ω，发电功率1 300 W；轻载时，负载电阻150 Ω，发电功率200 W。

4.2实验结果

图10为现有控制策略和新型控制策略下的实验结果，其中ua为负载A相电压，isa为发电机A相电流，if为发电机励磁电流，m为变换器调制比。

现有控制策略下，励磁电流恒定为2.9 A，此时m约为0.85。新型控制策略下，励磁电流通过闭环控制同样稳定在2.9 A，m稳定在0.85。傅里叶分析表明，图10a中负载电压幅值为143.3 V，THD为2.55%；图10b中负载电压幅值为142.8 V，THD为2.8%。负载为1 300 W时，这两种发电控制策略下，负载电压均能跟随给定，且波形质量较好，系统均能正常工作。

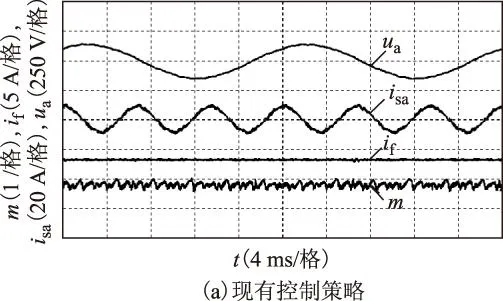
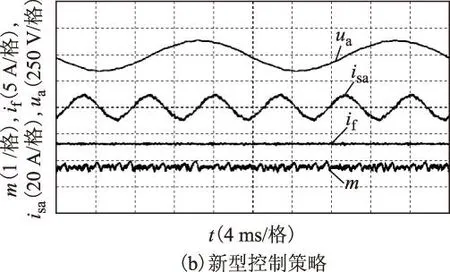
图10　负载1 300 W实验结果Fig.10　Experiment of control strategies under 1 300 W

轻载时负载侧功率因数为0.5。图11为轻载时两种控制策略实验结果对比。现有控制策略下，励磁电流不控制，仍为2.9 A，负载电压幅值约为210 V，不能跟随给定值，发电机电流波形畸变较为严重；新型控制策略下，励磁电流通过调节稳定在1.4 A，负载电压幅值为142.8 V，THD为3.25%，系统在轻载时同样能正常工作。

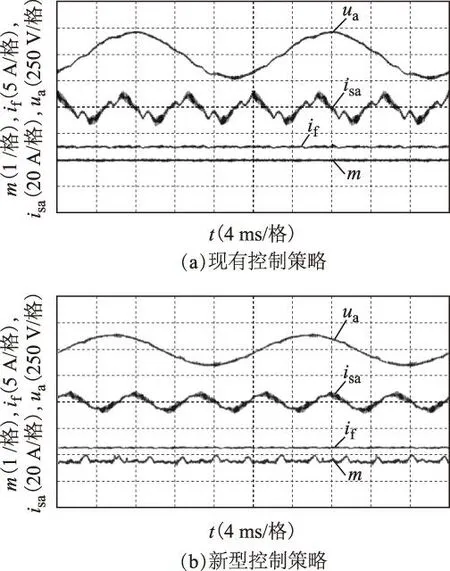
图11　负载200 W实验结果Fig.11　Experiment of control strategies under 200 W

图12和图13分别为现有控制策略和新型控制策略下负载从1 300 W切换至200 W，从200 W切换至1 300 W时的实验结果。新型控制策略下，负载切换后，系统经过几个周期很快就能恢复稳态。而现有控制策略下，轻载时负载电压不能稳定在给定值，发电机电流也会失控，系统不能正常工作。由实验结果可知，本文所提新型控制策略将发电功率范围由现有控制策略下额定值的50%～100%拓宽至15%～100%。

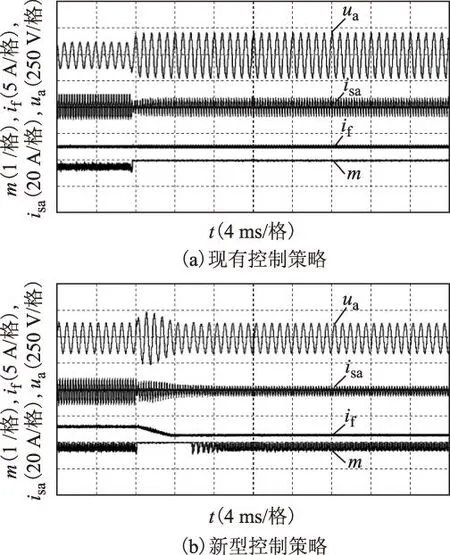
图12　负载从1 300 W切换至200 W实验结果Fig.12　Experiment of control strategies when load changes from 1 300 W to 200 W

图13　负载从200 W切换至1 300 W实验结果Fig.13　Experiment of control strategies when load changes from 200 W to 1 300 W

图14为系统分别在200 W、400 W、600 W、800 W、1 000 W、1 300 W时负载电压和发电机电流THD谐波分析曲线，随着负载功率的减小，发电机励磁电流和反电动势逐渐减小，电枢反应的影响逐渐增加，发电机电流THD逐渐增加，而负载电压THD均较小，波形质量较好。

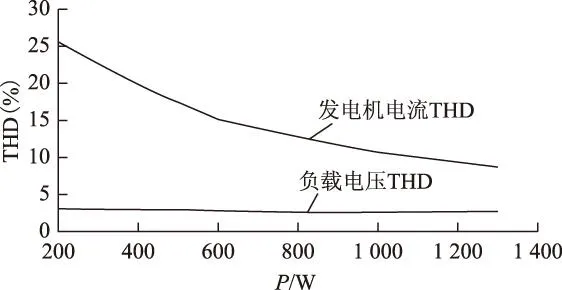
图14　不同负载时负载电压和发电机电流THD分析Fig.14　THD analysis of load voltage and generator current under different load

5结论

本文针对双级式矩阵变换器反向发电系统现有控制策略下系统不能在轻载和负载时正常工作的问题，探究了其原因，分析了现有控制策略下系统正常工作时的最小功率，提出一种能够拓宽发电功率范围的控制策略，使系统在额定负载和轻载时都能正常工作，将发电功率范围由现有控制策略下额定值的50%～100%拓宽至15%~100%。实验结果验证了该新型控制策略的正确性和有效性。

参考文献

[1]Mahat P，Chen Zhe，Bak-Jensen B.Review on islanding operation of distribution system with distributed generation[C]//2011 IEEE Power and Energy Society General Meeting，San Diego，San Diego，CA，2011：1-8.

[2]Xia Lili，Qiu Xiaoyan，Wei Xiwen，et al.Research of distribution generation planning in smart grid construction[C]//Proceedings of Asia-Pacific Power and Energy Engineering Conference，Chengdu，2010：1-4.

[3]Friedli T，Kolar J W，Rodriguez J，et al.Comparative evaluation of three-phase AC-AC matrix converter and voltage dc-link back-to-back converter systems[J].IEEE Transactions on Industrial Electronics，2012，59(12)：4487-4510.

[4]杨喜军，龚幼民，叶芃生.矩阵变换器的理论与应用[M].北京：机械工业出版社，2010.

[5]孙凯，周大宁，梅杨.矩阵式变换器技术及其应用[M].北京：机械工业出版社，2007.

[6]Andreu J，Kortabarria I，Ormaetxea E，et al.A step forward towards the development of reliable matrix converters[J].IEEE Transactions on Industrial Electronics，2011，59(1)：167-183.

[7]史明明，周波，魏佳丹，等.混合励磁同步发电机-矩阵变换器发电系统两级式电压闭环控制策略[J].中国电机工程学报，2012，32(3)：1-8.

Shi Mingming，Zhou Bo，Wei Jiadan，et al.Two-stage voltage closed loop control scheme for hybrid excited synchronous generator-matrix converter generation system[J].Proceedings of the CSEE，2012，32(3)：1-8.

[8]Liu Xiong，Loh P C，Wang Peng，et al.Distributed generation using indirect matrix converter in reverse power mode[J].IEEE Transactions on Power Electronics，2012，28(3)：1072-1082.

[9]Liu Xiong，Loh P C，Blaabjerg F，et al.Load sharing using droop control for parallel operation of matrix converters as distributed generator interfaces in isolated mode[C]//2012 IEEE Energy Conversion Congress and Exposition，Raleigh，NC，2012：962-968.

[10]Liu Xiong，Wang Peng，Loh P C，et al.Distributed generation interface using indirect matrix converter in boost mode with controllable grid side reactive power[C]//Proceedings of IEEE Conference on Power and Energy，Ho Chi Minh City，2012：59-64.

[11]Rodriguez J，Rivera M，Kolar J W，et al.A review of control and modulation methods for matrix converters[J].IEEE Transactions on Industrial Electronics，2012，59(1)：58-70.

[12]孙尧.矩阵变换器若干关键问题研究[D].长沙：中南大学，2010.

[13]Qin Xianhui，Zhou Bo，Wei Jiadan，et al.Distortion analysis and duty ratio correction algorithm for asymmetric modulation of two-stage matrix converter[J].IEEE Transactions on Industrial Electronics，2014，62(1)：351-362.

[14]何必，乔鸣忠，林桦，等.矩阵变换器占空比矢量理论及调制策略[J].电工技术学报，2011，26(S1)：56-64.

He Bi，Qiao Mingzhong，Lin Hua，et al.Duty-cycle space vector theory of matrix converter and its modulation method[J].Transactions of China Electrotechnical Society，2011，26(S1)：56-64.

[15]何必，乔鸣忠，林桦，等.矩阵变换器输入功率因数可调时的换流控制策略[J].电工技术学报，2012，27(7)：191-197.

He Bi，Qiao Mingzhong，Lin Hua，et al.Commutation strategies of matrix converter with adjustable input power factor[J].Transactions of China Electrotechnical Society，2012，27(7)：191-197.

[16]王兴伟，林桦，邓建，等.实际应用中的矩阵变换器空间矢量调制算法及优化调制模式[J].中国电机工程学报，2011，31(30)：7-15.

Wang Xingwei，Lin Hua，Deng Jian，et al.Optimization modulation pattern for space vector modulation method of matrix converter in practical application[J].Proceedings of the CSEE，2011，31(30)：7-15.

[17]陆晓楠，孙凯，李刚，等.双级矩阵变换器网侧功率因数的控制方法[J].电工技术学报，2010，25(10)：108-114.

Lu Xiaonan，Sun Kai，Li Gang，et al.Control method analysis of grid side power factor in two stage matrix converter[J].Transactions of China Electrotechnical Society，2010，25(10)：108-114.

[18]黄海涛，周波，秦显慧，等.双级矩阵变换器输入功率因数可调的载波调制策略[J].中国电机工程学报，2015，35(1)：177-184.

Huang Haitao，Zhou Bo，Qin Xianhui，et al.Carrier-based modulation strategy for two stage matrix converter with adjustable input power factor[J].Proceedings of the CSEE，2015，35(1)：177-184.

卞金梁男，1990年生，硕士研究生，研究方向为功率变换技术与矩阵变换器。

E-mail：bjlnuaa@nuaa.edu.cn

周波男，1961年生，教授，博士生导师，研究方向为新能源发电技术、航空电源系统、电机及其控制与功率变换技术。

E-mail：zhoubo@nuaa.edu.cn(通信作者)

作者简介

中图分类号：TM92

收稿日期2015-01-29改稿日期2015-12-10

国家自然科学基金(51177069)、江苏省高校优秀科技创新团队项目、江苏省研究生培养创新工程(KYLX_0269)和南京航空航天大学研究生创新基金(KFJJ201411)资助。