“目”字形耦合电感器的设计及应用

杨玉岗　万　冬　张凯强

(辽宁工程技术大学电气与控制工程学院　葫芦岛　1251051)



“目”字形耦合电感器的设计及应用

杨玉岗万冬张凯强

(辽宁工程技术大学电气与控制工程学院葫芦岛1251051)

摘要为适应新一代变换器低压、大电流和快速暂态响应的功率需求，提出一种“目”字形耦合电感结构，通过分析耦合电感的磁通分布，建立了磁路模型，从而得到自感、漏感和互感的计算公式，并给出耦合电感的设计方法。通过仿真和实验，证明了磁件模型的正确性，得出“目”字形耦合电感器具有加工简单、电感量大、磁通密度分布更均匀以及直流叠加特性好等优点，将其应用于交错并联磁集成双向DC-DC变换器，具有相电流纹波小及效率高等优点。

关键词：双向DC-DC变换器“目”字形耦合电感器耦合度交错并联磁集成

Design and Application of The “UUUU” Shape Coupled Inductor

YangYugangWanDongZhangKaiqiang

(Faculty of Electrical and Control EngineeringLiaoning Technical UniversityHuludao125105China)

AbstractIn order to meet the power needs of a new generation of low-voltage，high-current，and fast transient response converter，a “UUUU” shape coupled inductor structure is proposed.The flux distribution of the coupled inductor is firstly analyzed in order to establish the magnetic circuit model，and thus derive the formula for inductance，leakage inductance，and mutual inductance.Then the design method of coupled inductor is provided.Through simulation and experiments，the correctness of the magnetic component model is validated.The proposed “UUUU” shape coupled inductor has the characteristics of simple processing，large inductance，more uniform magnetic flux density distribution，and good DC superposition property.The “UUUU” shape coupled inductor can be applied to the interleaving bidirectional DC-DC converter with small phase current ripple and high efficiency.

Keywords：DC-DC converter，“UUUU” shape coupled inductor，coupling degree，interleaving magnetic integration

0引言

开关变换器是现代电能转换的重要组成部分，其性能直接关系到输出电能指标的高低。磁性器件(简称磁件，包括电感和变压器)在变换器中实现能量存储与转换、滤波和电气隔离等功能，是影响变换器体积、重量和效率的关键部分。因此，磁件的设计是变换器设计工作的重点[1-10]。

磁件的结构决定了其各方面性能。文献[1]提出的“EI”形耦合电感器将气隙开在中柱，两个绕组缠绕在两个侧柱上，最大程度上减小了两个绕组之间的磁阻，增大了两个绕组的互感，但气隙过于集中，磁通密度分布不均匀引起磁心损耗过大。

本文提出了一种“目”字形耦合电感器结构，建立了基本磁路模型和改进磁路模型，并给出了设计方法，通过三维电磁场有限元仿真与应用在交错并联DC-DC变换器的实验，验证了“目”字形耦合电感器具有磁通密度分布更均匀、直流叠加特性好以及相电流纹波小等优点。

1“目”字形耦合电感器建模

1.1“目”字形耦合电感器结构

本文提出的“目”字形耦合电感器结构如图1所示，耦合电感器由4个“U”字形铁心1和两相绕组2组成。此结构中间两个“U”字形铁心对接，呈环状，最大程度地提供了互感；上下两侧的两个“U”字形铁心提供了足够的漏感；所开的4个气隙增大了上下两侧的磁阻，能够增加通过互感的磁通量；结构对称，变换器采用交错并联技术，磁件的直流偏磁能够相互削减。

图1　“目”字形耦合电感器的磁通分布及磁路长度Fig.1　Flux distribution and magnetic circuit length of “UUUU” shape coupled inductors

图1中，φ1、φ2分别为两相绕组的主磁通，φc为漏磁通，a、b、c、d分别为各部分铁心长度(a=3b)，g1、g2分别为气隙长度，l1、l2、l3、l4分别为各部分磁路长度。用N表示绕组匝数，h表示铁心厚度。

1.2“目”字形耦合电感器的电路模型

图1中“目”字形耦合电感器的等效电路模型与传统耦合电感器相同，如图2所示。图中，M为两相电感绕组之间的互感，Lk1、Lk2分别为两相电感绕组的漏感，i1、i2分别为流过两相电感绕组的电流，Tr1为两相电感全耦合时的理想变压器模型。由于设两相电感对称且反向耦合，所以两相电感绕组的自感L1=L2=L，-1≤M/L≤0，并有

(1)

图2　两相耦合电感器的电路模型Fig.2　Circuit model of 2-phase coupled inductor

2“目”字形耦合电感器的磁路模型

2.1基本磁路模型

为了建立两相“目”字形耦合电感器的简化磁路模型，需首先分析其磁通分布。在忽略了各相绕组产生的通过外部空气的漏磁通和气隙边缘效应后，得到“目”字形耦合电感器的磁通分布如图1a所示，磁通所经过的各段磁路长度如图1b所示。

根据磁路欧姆定律得到两相“目”字形耦合电感器的基本磁路模型如图3a所示。图中，F1、F2分别为两相绕组的磁动势，F1=N1i1、F2=N2i2；R11、R12、R13、R14分别为各段磁路的磁阻；Rg1为g1的磁阻；Rg2为g2的磁阻。由于磁路左右对称，所以其磁阻也是对称的。将串联的磁阻合并，得到合并后的磁路模型如图3b所示。

图3　“目”字形耦合电感器的基本磁路模型Fig.3　Basic magnetic circuit model for “UUUU”shape coupled inductors

根据磁阻定义可得到图3a中气隙磁阻的计算公式为

(2)

图3a中各段铁心的磁阻计算公式为

(3)

式中，μ0为空气磁导率；μr为铁心材料的相对磁导率；gi为气隙长度；b为铁心宽度；h为铁心厚度；li为铁心长度。图3b中磁阻R1、R2和R3可用图3a中的磁阻表示

(4)

图4为“目”字形耦合电感器的磁路-电路等效模型。

图4　“目”字形耦合电感器的磁路-电路模型Fig.4　The magnetic circuit model for “UUUU” shape coupled inductors

图4中磁动势Ni1和Ni2(N1=N2=N)以及磁通φ1和φ2可表示为

(5)

为了方便计算，设

(6)

则磁动势Ni1和Ni2(N1=N2=N)以及磁通φ1和φ2可表示为

(7)

可得到磁通φ1和φ2的表达式为

(8)

由电磁感应定律，加在两个绕组上的电压V1和V2可表示为

(9)

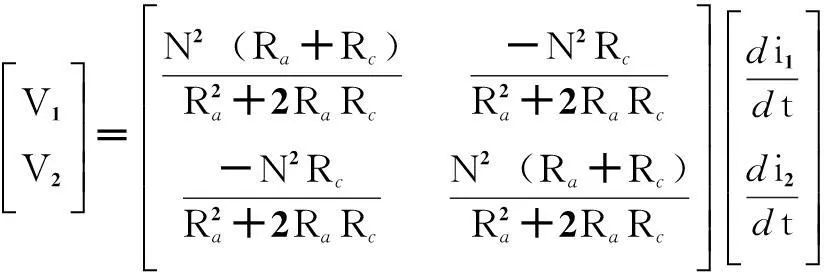
(10)

比较式(1)和式(10)，表征“目”字形耦合电感器的自感L1和L2、互感M以及漏感Lk1和Lk2分别为

(11)

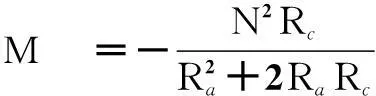
(12)

(13)

2.2改进磁路模型

为了提高上述磁路模型的精度，需要考虑所忽略的气隙磁阻的磁场边缘效应和绕组外面的空气漏磁通。于是根据图3得到两相“目”字形耦合电感器的改进磁路模型如图5所示。图中，气隙磁阻Rg1、Rg2中考虑了g1和g2的磁场边缘效应，磁动势N1i1和N2i2上并联了空气磁阻Rair1和Rair2，图5b是对图5a中串联磁阻合并后的模型。

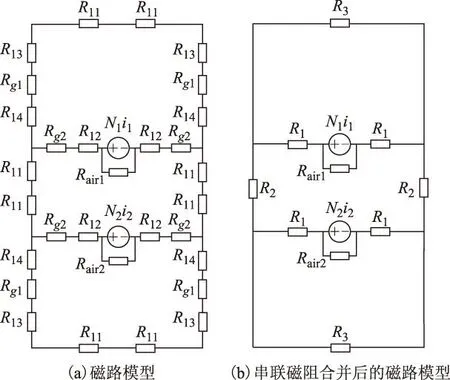
图5　“目”字形耦合电感器的改进磁路模型Fig.5　Improved magnetic circuit model for “UUUU” shape coupled inductors

2.2.1“目”字形铁心的磁轭气隙磁阻R′g1和R′g2

当考虑g1和g2的磁场边缘效应时，可求得图1中“目”字形耦合电感器气隙磁阻R′g1、R′g2[11]分别为

(14)

(15)

式中，d=N′d1+2δ，其中N′为绕组层数，d1为绕组厚度，δ为绕组与其窗口两侧之间所留的裕量。

2.2.2绕组外面的空气磁阻Rair

对“目”字形耦合电感器绕组产生的外部空气磁场进行分析，可得其近似磁力线分布如图6所示。图中矩形底座表示缠绕着宽度为w=2a-2b的绕组的“目”字形铁心磁柱，半圆柱表示磁力线通过的区域。

图6　耦合电感器绕组外面的空气磁力线分布Fig.6　Flux distribution in the air out of the coupled inductors

由图6及文献[12]的空间切割概念可得到“目”字形耦合电感器各相绕组产生的空气磁力线区域如图7所示，绕组产生的磁力线所通过的区域包括前、后两部分，其磁力线所遇到的磁阻分别为Rt和Rb，呈半圆柱型，由于前、后两面的绕组对称，故只画了一面。于是可得两相绕组的空气磁阻Rair1和Rair2为

Rair=Rair1=Rair2=Rt//Rb

(16)

图7　“目”字形耦合电感器绕组外面的空气磁阻Fig.7　Air reluctance outside the winding of“UUUU”shape coupled inductors

磁阻Rt和Rb的计算公式为

(17)

(18)

式中，Vt为磁阻区域的体积。

2.2.3改进磁路的电感计算

在得到各磁阻的计算公式后，可计算图4中改进磁路模型的绕组自感L1、L2和漏感Lk1、Lk2，若N1=N2=N，可得

(19)

(20)

3“目”字形耦合电感器的设计

通过上述分析，得到了“目”字形耦合电感器各部分尺寸与电感值和漏感值之间的关系，能够按照电路对电感的电感值和耦合度的要求，设计出所需的“目”字形结构耦合电感器，具体设计步骤如下。

3.1设计规格

设输入电压为Vin；输出电压为Vo；输出电流为Io；开关频率为fs；稳态输出电流纹波为ΔIo，暂态电流响应速度为Δi/ΔD。

3.2自感和漏感计算

由于ΔIo和Δi/ΔD不一定能同时满足，在设计双向DC-DC变换器时，应优先保证Δi/ΔD。为了满足Δi/ΔD，可求得漏感Lki为

(21)

式中，Lki为漏感，下标i=1,2。

为了满足ΔIo，可求得稳态电流纹波为

(22)

若ΔI′o≤ΔIo，说明设计的耦合电感不但满足变换器对暂态电流响应速度的要求，还满足变换器对稳态电流纹波的要求。若ΔI′o>ΔIo，说明所设计的电感仅达到了暂态电流响应速度的需求，而不能达到稳态电流纹波的要求。自感L为

(23)

式中，k为耦合系数，-1≤k≤0。

3.3铁心尺寸计算

“目”字形铁心磁柱在不饱和限制条件下的最大磁通密度[13]为

(24)

式中，Φ为直流磁通；Δφ为交流磁通。所以

(25)

式中，A为“目”字形耦合电感器绕组缠绕磁心的截面积；Bmax为铁心不饱和前提下能够承受的最大磁通密度。

由式(24)可得到A的值，进而根据A=b×h得到a、b和h的值，如图1b所示。将式(21)和式(23)求得的漏感和自感代入式(19)和式(20)可得到g1和g2。

4实验和仿真结果分析

为了验证前面的理论分析，并分析磁件特性，分别进行了仿真和实验。

设计规格为：Buck工作模态下，输入电压VH=10 V，输出电压VL=2 V，输出电流值Io=4 A；Boost工作模态下，输入电压VL=10 V，输出电压VH=14 V，输出电流值Io=2A，fs=100 kHz。控制电路采用DSP2812，相电流的测试采用闭环霍尔电流传感器CHB-25NP，匝比n=1/1 000，测试电阻RM=1 000 Ω。根据电路对电感的要求，制作了传统“EI”和“目”字形耦合电感器样品如图8所示。

图8　磁件样机Fig.8　Magnetic prototype

4.1磁件样机制作

根据第二节的内容计算磁件。设计的电感采用TP4材料制作铁心，垫气隙纸来加工“目”字形耦合电感器的气隙，采用一个“E”形铁氧体和一个“I”形铁氧体制作传统“EI”形耦合电感器，如图8a所示；采用相同材料，设定图1b中a、b、d、h分别为6 mm、2 mm、4 mm、6 mm，制作“目”字形耦合电感器，如图8b所示。

为了便于比较“EI”形耦合电感器和“目”字形耦合电感器的性能，两者的绕组及磁性尺寸应相同，匝数相同，调整气隙大小使得两种耦合电感器的漏感相等。

由图8可见，“目”字形耦合电感器和“EI”形耦合电感器均可进行组装加工：绕组绕在标准圈骨架上，再将其套在磁心柱上。“目”字形耦合电感器能够通过垫气隙纸的方式来加工气隙。

4.2电感值比较

图9为两种磁件开不同气隙时绕组的自感和互感。“目”字形磁件的气隙范围为0～0.2 mm，“EI”形磁件的气隙范围为0～0.4 mm。

从图9中可看出，“目”字形耦合电感器气隙长度是“EI”形耦合电感器气隙长度的一半时，两磁件漏感接近相等，此时，“目”字形耦合电感器的自感、互感和耦合系数均大于“EI”形耦合电感器，且气隙长度越大，相差越大。

图9　电感值比较Fig.9　Inductance value comparison

4.3铁心的磁通密度分布

电感设计要求在电感通过最大电流时，铁心的最大工作磁通密度不能大于铁心材料磁性饱和的磁通密度。利用ANSYS电磁场仿真软件对两种磁件建模。磁心中磁通密度分布不均匀可能会导致电感较易饱和，也会引起损耗增加。两相交错并联DC-DC变换器运行时，两通道电感电流的直流分量接近相等。给两种耦合电感器的绕组中都通入3 A的电流，“EI”形磁件上下气隙为0.05 mm，中柱气隙为0.2 mm，“目”字形磁件上下气隙为0.2 mm，中柱气隙为0.05 mm，仿真其铁心工作磁通密度，仿真结果如图10所示。

图10　磁通密度矢量Fig.10　The magnetic flux density distribution

由图10可见，两种铁心的最小工作磁通密度相同，而“目”字形结构铁心的最大工作磁通密度仅为“EI”形结构铁心的53%，说明“目”字形结构的电感的磁通密度分布较均匀，铁心更不易饱和。“EI”形结构的大部分磁通密度为0.081 T，“目”字形结构铁心整个中间部分的磁通密度几乎为零，大部分磁通密度为0.036 T，“目”字形结构的耦合电感器整体磁通密度更低。

4.4直流叠加特性比较

“目”字形耦合电感器整个中间部分的磁通密度几乎为零，本质在于其直流叠加特性。将图10b中“目”字形耦合电感器绕组减少一组进行仿真，仿真结果如图11所示。图11a为“目”字形耦合电感器一个电感工作，图11b为“目”字形耦合电感器两个电感工作。

图11　耦合电感器的磁感应强度仿真图Fig.11　Flux density simulation results of coupled inductors

从图11中可明显看出，“目”字形耦合电感器单通道工作过程中，耦合电感器的磁通主要分布在中间部分，两相电感工作时，中间部分磁通很低。说明：两电感集成后，铁心中间部分的直流磁通相互削减；最大磁通密度点降低，耦合电感器铁心更不易饱和；能够在耦合电感器铁心不饱和前提下，减小电感的体积，降低其重量。

结合图10可看出，“目”字形耦合电感器直流叠加特性好于“EI”形耦合电感器，能更大程度地减小耦合电感的体积。

4.5“目”字形耦合电感器的临近扩散磁场

扩散磁通有很多危害：①扩散磁通引起周围电路的电磁干扰；②扩散磁通引起周围电路损耗；③扩散磁通引起铜箔线圈导体涡流，减少导体有效截面积，增加导体损耗，或引起导体局部过热。

通过仿真来比较两种电感器之间的扩散磁通。图12为耦合电感器的磁通矢量图。从图中可看出气隙对变换器扩散磁通的影响。

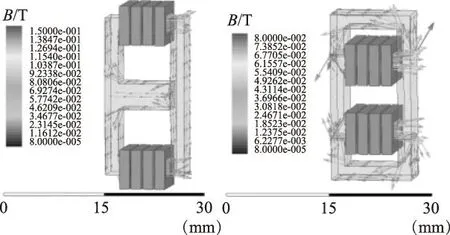
图12　磁通矢量图Fig.12　Flux vector coupled inductors

“EI”形耦合电感器是将气隙放在中柱，气隙被包住，磁场泄露较小，而“目”字形耦合电感器气隙分布在侧边，由于气隙面存在磁压降，所以在气隙周围的空间就会有磁场泄露，这是较“EI”形耦合电感器的不好之处，但扩散的范围不大，局限在气隙附近。

由于两个气隙的磁动势方向相反，从大范围上看，两个磁动势是相抵消的，因此其扩散磁通值局限在气隙附近，不会形成大范围的扩散影响。

相比之下，“目”字形耦合电感器气隙对称，磁动势方向相反，磁动势能够两两抵消；气隙长度更短，扩散磁通范围更小，从而减小周围电子设备干扰，减小线圈涡流损耗，提高变换器效率。

4.6“目”字形耦合电感器的应用

所提出的“目”字形耦合电感器应用在双向DC-DC变换器Buck和Boost工作模式下。交错并联双向Buck变换器的电路图如图13所示，将两个分立电感器用“目”字形耦合电感器替换。

按照第3节中的设计规格，设计一个两相交错并联双向DC-DC变换器如图14所示，测试第三节中设计的“目”字形耦合电感器和传统的“EI”形耦合电感器，测试两种不同结构的耦合电感器运行在双向DC-DC直流变换器中，结果如图15所示。表1“目”字形耦合电感器的电感值，匝数N=4，气隙长度g1=0.25 mm，g2=0.02 mm。

图14　实验样机与测试系统Fig.14　Prototype and its test system

图15　两种耦合电感器应用于双向DC-DC变换器的相电感电流波形Fig.15　Phase inductor current waveforms of two kinds of coupled inductors applied in bidirectional DC-DC converter

基本磁路模型改进磁路模型有限元仿真电感值/μH误差(%)电感值/μH误差(%)电感值/μH误差(%)样机实验/μH自感1.7725.61.9219.32.432.12.38互感-1.4321.4-1.4719.2-1.851.6-1.82漏感0.3439.20.4521.20.571.80.56

由图15可见，在Buck和Boost两种模态下，采用“目”字形铁心结构电感的电流纹波比采用“EI”形铁心结构电感的电流纹波小，开关管开通和关断时的电流尖峰更小。

将设计的两种耦合电感器分别应用在双向DC-DC变换器中，改变负载值，计算不同负载时变换器的电能传输效率，并绘制成图16。双向DC-DC变换器工作在Buck模态下，当负载电流为0.5 A时，应用“EI”形耦合电感器的电路效率只有57.8%，而此时应用“目”字形耦合电感器的变换器效率高为58.8%，两个耦合电感器工作在Buck模式的最大效率差为1.5%。双向DC-DC变换器工作在Boost模态下，当负载电流为0.2 A时，应用“EI”形耦合电感器的电路效率只有59.2%，而此时应用“目”字形耦合电感器的变换器效率高为60.3%，两个耦合电感器工作在Buck模式的最大效率差为1.1%。由此证明应用“目”字形耦合电感器可有效提高电路的效率。

图16　耦合电感器应用于双向DC-DC变换器的效率对比图Fig.16　Comparison of efficiency used in bidirectional DC-DC converter with coupled inductor

5结论

通过以上理论推导，仿真和实验分析表明，在相同磁心尺寸下，相比于“EI”形耦合电感器，“目”字形耦合电感器具有以下特点：

1)互感、自感和耦合系数更大。

2)磁心的磁通密度分布更均匀。

3)扩散磁通范围小、气隙对称、能相互抵消。

4)应用在双向DC-DC变换器工作，相电流纹波更小，并有效提高了电路的效率。

参考文献

[1]杨玉岗，李洪珠，王建林，等.可削减直流偏磁集成磁件在DC/DC变换器中的应用[J].中国电机工程学报，2005，25(11)：50-54.

Yang Yugang,Li Hongzhu,Wang Jianlin,et al. Research on the application of an integrated magnetics whose DC-basc can be reduced in DC-DC converter[J]. Proceedings of the CSEE,2005，25(11)：50-54.

[2]Bai H，Mi C.Eliminate reactive power and increase system efficiency of isolated bidirectional dual-active-bridge DC-DC converters using novel dual-phase-shift control[J].IEEE Transactions on Power Electronics，2008，23(6)：2905-2914.

[3]García O，Zumel P，de Castro A，et al.Automotive DC-DC bidirectional converter made with many interleaved buck stages[J].IEEE Transactions on Power Electronics，2006，21(3)：578-586.

[4]Xie Yanhui，Sun Jing，James S.Power flow characterization of a bidirectional galvanically isolated high-power DC/DC converter over a wide operating range[J].IEEE Transactions on Power Electronics，2010，25(1)：54-66.

[5]Liang T J，Chen S M，Yang L S，et al.Ultra-large gain step-up switched-capacitor DC-DC converter with coupled inductor for alternative sources of energy[J].IEEE Transactions on Circuits and Systems，2012，59(4)：864-874.

[6]Yang Yugang，Yan Dong，Lee F C.A new coupled inductors design in 2-phase interleaving VRM[C]//IEEE 6th Power Electronics and Motion Control Conference，Wuhan，China，2009：344-350.

[7]杨玉岗，于庆广，李洪珠，等.四相电压调整模块中平面型可消除直流偏磁集成磁件研究[J].中国电机工程学报，2006，26(24)：179-185.

Yang Yugang，Yu Qingguang，Li Hongzhu，et al.Research on planar integrated magnetics whose DC-bias can be eliminated in 4 phase interleaving VRM[J].Proceedings of the CSEE，2006，26(24)：179-185.

[8]陈为，卢增艺，王凯.电压调节模块耦合电感性能分析与设计[J].电工技术学报，2009，24(1)：127-132.

Chen Wei，Lu Zengyi，Wang Kai.Performance analysis and design of voltage regulator module with coupled inductors[J].Transactions of China Electrotechnical Society，2009，24(1)：127-132.

[9]杨玉岗，冯本成，韩占岭，等.四相VRM 中无直流偏磁集成磁件[J].电工技术学报，2012，27(4)：88-93.

Yang Yugang，Feng Bencheng，Han Zhanling，et al.Non DC-bias integrated magnetic components for 4-phase VRM[J].Transactions of China Electrotechnical Society，2012，27(4)：88-93.

[10]李洪珠，郝文慧，杨玉岗.无气隙可改变耦合度阵列式集成磁件在交错并联变换器中的应用[J].电工技术学报，2007，22(7)：98-102.

Li Hongzhu，Hao Wenhui，Yang Yugang.Application of changeable coupling degree array integrated magnetics with no air gap to staggered-shunt converter[J].Transactions of China Electrotechnical Society，2007，22(7)：98-102.

[11]Balakrishan A，Joines W，Wilson T.Air-gap reluctance and inductance calculations for magnetic circuits using a schwarz-christoffel transformation[J].IEEE Transactions on Power Electronics，1997，12(4)：654-663.

[12]Hoke A，Sullivan C R.An improved two-dimensional numerical modeling method for E-core transformers[C]//Proceedings of the IEEE Applied Power Electronics Conference，Dallas，US，2002，1：151-157.

[13]刘学超.平面磁集成电压调节模块建模方法及磁耦合微分几何解耦控制[D].广州：华南理工大学，2006.

杨玉岗男，1967年生，博士，教授，博士生导师，研究方向为电力电子及其磁集成技术。

E-mail：yangyugang21@126.com

万冬女，1990年生，硕士研究生，研究方向为智能电器理论及应用、电力电子磁集成技术。

E-mail：16377927@qq.com(通信作者)

作者简介

中图分类号：TM55

收稿日期2015-01-26改稿日期2015-12-15

国家自然科学基金(51177067，U1510128)和辽宁省教育厅重点实验室基础研究项目(LZ2015045)资助。