多模块APF并联系统高频谐波环流分析与控制

许　胜　费树岷　赵剑锋　黄允凯

(1.东南大学复杂工程系统测量与控制教育部重点实验室　南京　210096

2.泰州学院　泰州　225300)



多模块APF并联系统高频谐波环流分析与控制

许胜1，2费树岷1赵剑锋1黄允凯1

(1.东南大学复杂工程系统测量与控制教育部重点实验室南京210096

2.泰州学院泰州225300)

摘要有源电力滤波器(APF)的高频开关谐波由于通常不包含在电流闭环控制回路内而表现为电压源特性，造成多模块APF模块间的高频谐波环流，增加了系统功率损耗，降低了系统稳定性和控制精度。针对上述问题，对多模块APF并联系统高频谐波环流进行研究，通过构建系统高频谐波环流数学模型，详细分析了环流的形成机理及其影响，并分析了模块输出滤波器(OF)对环流的影响。最后，提出一种多模块APF协调控制方法，以抑制系统高频谐波环流。理论分析和实验结果表明：各模块SPWM载波不同步是高频谐波环流的主要成因；高频环流不流入电网系统；OF能抑制各模块高频谐波电流的非环流分量，而对于环流分量并无明显的抑制效果，相反会降低系统的稳定性；所提模块化APF并联协调控制方案可有效抑制系统的高频谐波环流。

关键词：多模块有源电力滤波器高频谐波环流载波相移SPWM输出滤波器协调控制

Analysis and Control of High-Frequency Harmonic Circular Currents in Multi-Module APF Parallel System

XuSheng1，2FeiShumin1ZhaoJianfeng1HuangYunkai1

(1.Key Laboratory of Measurement and Control of CSE Ministry of Education Southeast UniversityNanjing210096China2.Taizhou UniversityTaizhou225300China)

AbstractBecause the high-frequency switching harmonics of the active power filter (APF) are generally not included in the closed current control loop，they will have the characteristics of voltage source，which may cause the high-frequency harmonic circular currents in the modules of multi-module APF.These harmonic circular currents will increase the power loss and reduce the system stability and control precision.To solve above problems，through building the circular current mathematical model，the formation mechanism of the circular current and its influences are analyzed in detail.Furthermore，the influences of the output filters (OF) on the circular currents are researched.Finally，a coordinated control strategy to suppress the circular currents is introduced.The theoretical analysis and experimental results show that：Firstly，the primary cause of the circular currents is the asynchronization of SPWM carrier waves；Secondly，the circular currents do not flow into the power system；thirdly，the OF can inhibit the non-circular part of the high-frequency harmonic currents，but it is ineffective to the circular part and will undermine the system stability；Finally，the circular currents can be inhibited effectively by the coordinated control method proposed in this paper.

Keywords：Multi-module APF，high-frequency harmonic circular currents，CPS-SPWM，output filter，coordinated control

0引言

当前，随着我国工业化规模的扩大，越来越多的非线性负荷被投入使用，大量谐波流入电网，传统单个有源电力滤波器(Active Power Filter，APF)的容量和调节能力已不能满足电网谐波治理要求[1，2]。因此，人们研究并发展了一些大容量APF结构模式，比较典型的有混合型APF[3]、多电平APF[4]以及模块化APF[5]等。其中，混合型APF无源部分参数设计难度大，且易发生谐振；多电平APF单机容量虽大，但电路控制复杂、可靠性要求及造价较高。相比之下，多模块并联结构的APF便于容量扩展，可实现故障冗余，具有应用灵活及可靠性高等优势。

然而，多模块APF运行时，会在模块间存在高频谐波环流。由于各模块高频开关谐波的产生主要与开关频率和调制比(SPWM调制方式)或滞环宽度(滞环控制方式)相关，通常不存在于电流闭环控制回路内，因而不具有受控电流源特性，而呈现电压源特性，这是产生高频环流的主要原因。另一方面，为了避免高频谐波造成电网的二次污染，APF通常在网侧安装输出滤波器(Output Filter，OF)，而在实际工程中发现，当OF的类型及其参数配置不同时，系统高频环流特性也不尽相同。实际上，由于OF的滤波和谐振特性[6，7]，必然会对高频环流造成影响。模块间存在的高频谐波环流交互作用，增加了系统功率损耗，降低了系统的稳定性和控制准确度。

目前，国内外在模块化变流器环流方面的研究主要集中在并网逆变器[8-10]和不间断电源(Uninterruptible Power Supply，UPS)[11]领域，而针对模块化APF的环流研究[12-14]相对较少，其中文献[13]仅从具体开关模态的角度分析了由载波相移导致的环流原因。

本文对多模块APF并联系统高频谐波环流进行了研究，首先建立了基于SPWM载波角频率的各APF模块输出电压数学模型；在此基础上，通过构建并联系统环流数学模型，详细分析了高频环流的形成机理及其对系统的影响，并以LC型滤波器为例分析了OF对系统环流的影响。最后，提出一种多模块APF并联系统的协调控制方法，以抑制高频谐波环流。

1基于SPWM载波角频率的APF模块输出电压数学模型

1.1模块化APF系统结构

为了简化分析，取并联模块数N=2，主电路结构如图1所示。图中，ug为电网电压；Rg、Lg分别为电网等效电阻和电感；Li、RL分别为负载支路等效电感以及整流器电阻负载；L为模块网侧连接电感；ika、ikb、ikc分别为模块三相输出电流，uka、ukb、ukc分别为模块三相输出相电压，isa、isb、isc分别为并联系统电流，k=1，2；Udc为直流侧电压。

为了简化分析并突出对并联系统高频谐波环流的研究，对系统作如下特征设定：①电网三相电压对称无畸变；②各模块元件参数一致，直流侧电压相同；③各模块具有相同的调制波函数；④模块输出相电压参考点选择直流电压中心点o，以避免选择参考点o′所带来的直流分量，而两种参考点下电压交流谐波特性一致。鉴于装置的三相对称性，下面均以a相为例分析问题，并且省略下标a。

图1　多模块APF并联系统结构Fig.1　The circuit structure of multi-module APF

1.2APF模块输出电压数学模型

为了精确分析APF并联系统高频谐波环流的形成机理，首先建立基于SPWM载波角频率的各APF模块输出电压数学模型，并采用基于对称规则采样法的SPWM脉冲生成方法。图2为一个载波周期Tc中SPWM脉冲的生成原理及输出相电压波形。图中ωc为载波角频率，Vrm为载波峰值，us为正弦调制波，θ1、θ2分别为一个载波周期2π中脉冲电压u的边沿时刻。

图2　基于对称规则采样法的APF模块输出相电压Fig.2　The output phase voltage of APF modules based on regular sampling

由图2可见，在载波谷底处(t1时刻)采样一次正弦调制波us，并用采样数值与载波相比较生成触发脉冲，该触发脉冲触发IGBT开关，形成输出电压u。

由于APF补偿n(≥2)次谐波电流，相应地，各相输出电压调制波中包含同样次数的谐波分量。本文根据线性叠加原理，任取某一单次补偿谐波分析问题，该谐波调制波函数us定义为

us=Umsin(ωst+φ)

(1)

式中，Um、ωs、φ分别为调制波的幅值、角频率和初相角，令调制比M=Um/Vrm。

根据图2，可求得θ1、θ2的取值

(2)

结合式(2)和图2，列出u一个载波周期上的表达式为

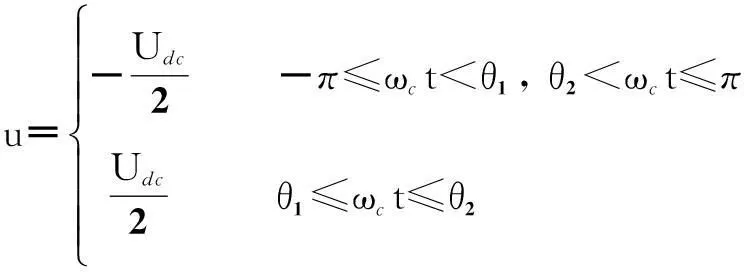
(3)

将u展开成Fourier级数形式

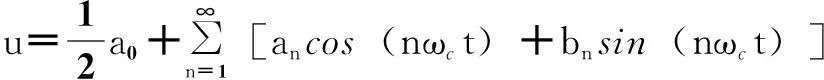
(4)

式中(具体过程略)

a0=MUdcsin(ωst1+φ)

(5)

(6)

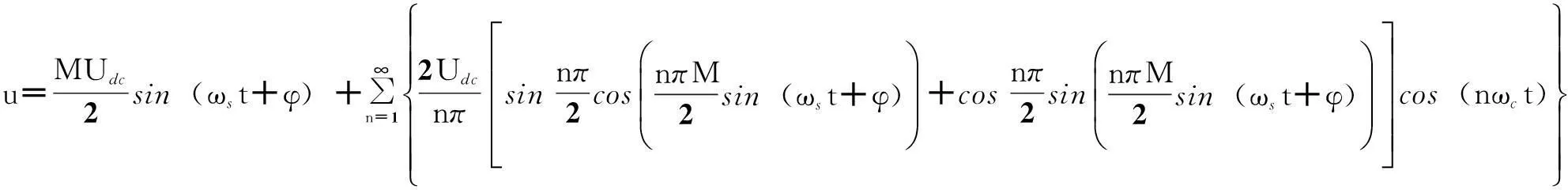
(7)

观察式(7)可见，u由两部分组成，这里分别记为um和un，其中

(8)

(9)

分析式(9)，um与载波ωc无关，仅与us和M相关，反映的是us相关信息，这里称之为低频调制分量；而un不仅与us和M相关，还取决于载波角频率ωc，这里称为高频开关分量。

2多模块APF并联系统高频谐波环流机理及其影响分析

2.1APF并联系统高频谐波环流数学模型

APF模块的高频开关谐波采用电压源和电抗串联的等效模型，参照图1，构建并联系统高频谐波单相等效电路，如图3所示。

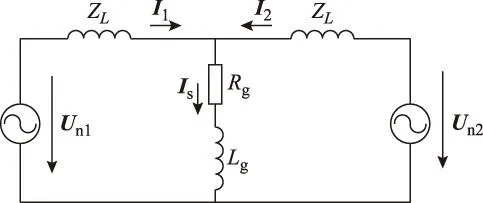
图3　并联系统高频谐波单相等效电路Fig.3　The high-frequency single-phase equivalent circuit of the parallel system

图3中，Un1、Un2分别为两并联模块等效高频谐波电压源；ZL为网侧串联电抗；I1、I2、Is分别为模块1和模块2输出电流以及并联系统电流。定义Zs为系统等效阻抗，对应系统等效电阻Rg和电感Lg。

根据图3可解出I1、I2、Is(具体过程省略)

(10)

根据式(10)，定义

(11)

2.2系统高频谐波环流机理及其影响分析

根据式(10)和式(11)，分析高频环流形成机理及其影响。

1)高频环流形成机理及其特性分析

I1、I2分别由两部分组成：第一部分仅与模块各自输出电压Un1、Un2相关，即I11、I22；第二部分与并联模块输出电压的差值ΔUn=Un1-Un2相关，即I12、I21，且I12=-I21。显然，电流I12、I21为Un1、Un2相互作用引起的环流。

鉴于对称性，下面以I12为例分析高频环流的形成机理及其特性。

设模块2的SPWM载波相位滞后模块1为φc，0≤φc<2π，则根据式(9)可得

Δun=un1-un 2=

(12)

分析式(12)中cos(nωct)-cos(n(ωct+φc))， 其中n=1，2，3，…，可得出以下结论：只有当φc=0，即模块1和模块2的载波同步时，才会有Δu=0，此时环流i12=0；而当载波不同步时，i12≠0，即模块间存在高频环流。

2)高频谐波环流影响分析

下面进一步分析SPWM载波移相及高频谐波环流对并联系统的影响。

根据式(9)，定义两模块高频谐波电压之和为∑un， 则

∑un=un1+un 2=

(13)

分析式(13)中cos(nωct)+cos(n(ωct+φc))， 其中n=1，2，3，…，可得：①当φc=0，即两模块的载波同步时，∑un是单个模块高频谐波电压的2倍，此时系统电流is中的高频谐波含量最高；②当φc=π时，即模块2的载波相位滞后模块1为π时(对应Tc/2)，有

k=1,2,3,…

此时，式(13)变换为

∑un=

(14)

由式(14)可知，φc=π时，is中的高频开关谐波含量相比于单个模块，消除了奇数倍载波频率ωc的谐波含量，主要分布在2倍的载波频率即2ωc附近，此时is中的高频谐波含量最低。

实际上，上述方法常用来消除并联系统电流中的谐波分量，即载波相移SPWM(Carrier Phase-Shifted SPWM，CPS-SPWM)技术，当并联模块数为N时，各单元载波相互错开时间Ts=Tc/N，即载波相位依次滞后2π/N，此时可消除Nωc以下的高频谐波分量[15，16]，限于篇幅这里不再做详细分析。但由式(12)的分析可知，载波移相又会在并联模块间造成环流。

根据图3，并结合式(10)和式(11)，可得

Is=I1+I2=I11+I22

(15)

由式(15)可知，并联系统电流is中并不包含存在于并联模块间的环流，即高频谐波环流对电网没有影响。

3输出滤波器对系统高频环流的影响分析

常见的APF输出滤波器包括L型、LC型、LCL型以及高通滤波器等。本节以LC型滤波器为代表分析输出滤波器对系统环流的影响。

采用LC型输出滤波器的APF并联系统高频单相等效电路如图4所示。

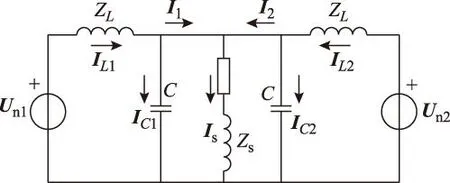
图4　基于LC滤波器的并联系统高频单相等效电路Fig.4　The high-frequency single-phase equivalent circuit based on the LC filter

图4中，C为滤波电容，与电抗L组成LC滤波电路，忽略电感电容上的电阻；IL1、IL2分别为两模块装置侧(滤波器前)输出电流；IC1、IC2分别为流过两模块滤波电容的电流；I1、I2分别为两模块网侧(滤波器后)输出电流。

根据图4可解出IL1、IL2、I1、I2、Is，鉴于对称性，本文仅列出IL1、IC1、I1和Is的电流表达式

(16)

根据式(16)，分析LC滤波前后的输出电流IL1和I1，两者中仍存在与并联模块输出电压的差值ΔUn=Un1-Un2相关的分量，该电流即为存在于并联模块之间的高频谐波环流，参照式(11)，分别定义为IL12和I12

(17)

对于高频谐波环流IL12和I12的形成机理及其影响分析，同第2.2节。由式(16)和式(17)可知，当载波同步，并联模块输出电压差值ΔUn=0时，环流i12=iL12=0，本节重点分析当环流存在时，LC滤波器对环流的影响。

将式(17)以传递函数的形式来表示

(18)

式中

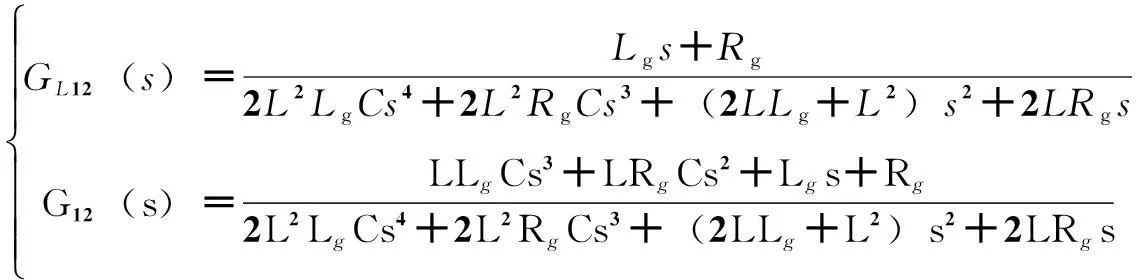
同理，根据式(11)中的I12，定义未加LC滤波器的环流传递函数G(s)为

(19)

画出G(s)、GL12(s)和G12(s)的Bode图，如图5所示，各参数取值参照表1。

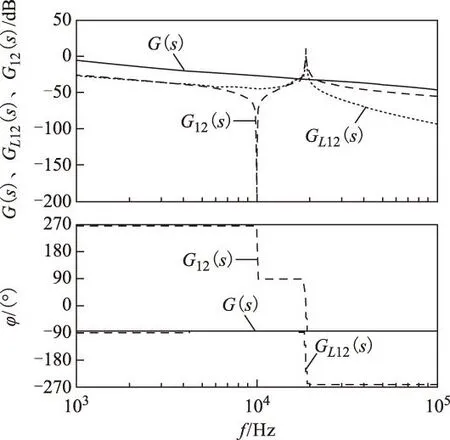
图5　G(s)、GL12(s)和G12(s)的Bode图Fig.5　The Bode diagram of G(s)，GL12(s) and G12(s)

参数数值模块网侧连接电感L/mH0.5滤波电容C/μF0.5电网等效电感Lg/mH0.1电网等效电阻Rg/mΩ20开关频率(采样频率)fs/kHz10

分析图5，GL12(s)和G12(s)出现明显的谐振，且在谐振处相角急剧下降，GL12(s)在谐振幅值第二次穿越0 dB时刻，相角裕度接近-90°，系统进入不稳定状态。针对该问题，实际工程中可通过增加LC滤波器阻尼电阻的方法抑制谐振，提高系统的稳定裕度，限于篇幅不再赘述。此外，比较G(s)与G12(s)的幅频特性可知，LC滤波器对高频环流基本没有抑制效果。

4APF并联系统高频环流控制

4.1APF并联系统高频环流抑制方法

由以上理论分析可知，并联系统高频谐波环流的主要成因是各模块输出高频开关谐波电压存在偏差。因此，要消除高频环流，应保证各模块输出电压严格一致，理论上必须具备以下条件：①各模块调制波函数us及调制比M相同，即各模块的谐波补偿目标一致；②各模块的SPWM载波在频率和相位上一致。

相应地，为了抑制并联系统高频谐波环流，可采取下列相关措施：

1)在各模块元件参数一致性的情况下，增强各模块控制系统的同步性，包括信号检测、控制算法实现以及各模块SPWM载波的同步性等。

以载波同步性为例，如果各模块载波的生成相互独立，由于各模块控制计数器的相对误差，载波之间的相位会出现周期性的相对运动，从而造成环流幅值周期性波动，这一点已通过实验验证。

2)保证各独立模块直流电压控制对同一电压参考值的精确跟踪，抑制由各模块的Udc不平衡所引起的环流。

3)由式(11)和式(12)可知，通过增加网侧串联电抗值ZL以及降低直流侧电压值Udc，亦可降低并联系统环流。其中：

(1)增加交流电抗值可降低环流，存在两种方法：一种是直接加大电感值L，但同时会降低APF电流跟踪控制的响应速度，特别是对高次补偿谐波电流；另一种方法是通过提高开关频率fs以提高相应电抗值2πfsL，但这受限于数字处理器运算速度以及开关管的最大开关频率。

(2)同理，降低Udc会降低电流控制响应速度，可考虑采用空间矢量脉宽调制(Space Vector PWM，SVPWM)等直流侧电压利用率高的控制算法。

4.2APF并联控制系统设计

根据4.1节高频谐波环流抑制措施，提出如下APF并联系统协调控制方法，如图6所示。

图6　多模块APF并联系统协调控制策略 Fig.6　Coordinated control strategy of multi-module APF

参照图6，协调控制系统采用分布式控制模式，由主控制和各模块底层控制组成。

1)主控制系统

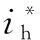
2)底层控制系统

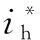
根据上述分析，可知所提模块化APF协调控制系统具有以下特点：

1)谐波电流检测由主控制器统一完成，避免了各模块控制器单独检测误差，保证了谐波检测的同步性。

2)采用SVPWM控制策略，直流电压利用率高，相比于常规的SPWM控制方法，直流电压可降低15.47%，因此，可适当降低直流侧电压值。

3)各模块电流控制在统一同步信号的控制下进行，保证了控制算法实现的同步性和SVPWM脉冲生成载波的同步性。

结合4.1节可知，上述控制系统特征可有效降低并联系统高频环流的产生。

5实验分析

实验电路模型参照图1，仍以两模块并联系统为例，主电路结构简图如图7所示，其中图7a、图7b分别设置了L型和LC型滤波器，以分析输出滤波器对环流的影响。实验电路参数设置参照表1，系统电压为400 V。

图7　实验主电路结构简图Fig.7　The simplified experimental circuit structure

1)采用L型滤波器(图7a)

图8、图9分别为载波同步和移相1/2载波周期两种情况下，装置侧(采样点①)电流i1和并联系统侧(采样点②)电流i2为波形图。

(1)比较图8和图9中的电流波形i1，可见，移相后的i1中含有较多的高频谐波分量。由第2.2节环流机理的理论分析可知，产生较多高频谐波电流的主要原因是载波不同步时并联模块间存在高频环流，该环流对应式(11)中的i12或i21。

(2)比较图8和图9中的系统电流波形i2，可见，图9所示载波移相后的i2中包含的高频谐波分量远小于图8所示载波同步时i2中包含的高频谐波分量。该结论符合第2.2节中有关并联系统电流is的理论分析结论，即采用载波移相技术可消除Nωc以下的高频开关分量，且实验结果进一步表明，模块间的环流对模块并联后系统电流没有影响。

图8　载波同步时装置侧和并联系统侧电流波形图Fig.8　Currents on the side of device and parallel system when modulated carrier waves synchronous

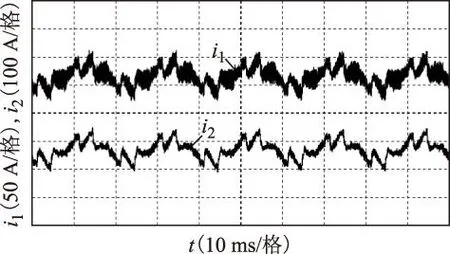
图9　载波移相时装置侧和并联系统侧电流波形图Fig.9　Currents on the side of device and parallel system when modulated carrier waves asynchronous

2)采用LC型滤波器(图7b)

图10、图11分别为载波同步和移相1/2载波周期两种情况下，模块装置侧LC滤波器前(采样点①)电流i1和LC滤波器后(采样点②)电流i2的波形图。

(1)由图10可见，当载波同步时，LC滤波器基本滤除了开关频率附近的高频开关谐波电流分量。

(2)由图11可见，当载波移相时，LC滤波器对高频电流分量基本没有滤波效果。该实验结果符合第3节相关理论分析结论。

图10　载波同步时LC滤波器前后电流波形图Fig.10　Currents on both sides of the LC-filter when modulated carrier waves synchronous

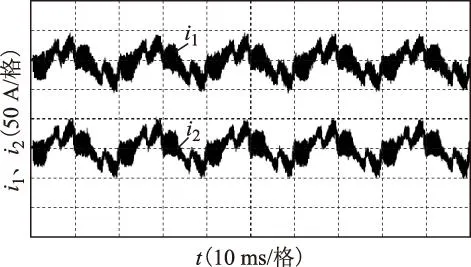
图11　载波移相时LC滤波器前后电流波形图Fig.11　Currents on both sides of the LC-filter when modulated carrier waves asynchronous

图12为载波移相时，模块装置侧(采样点①)电流i1和并联系统侧(采样点③)电流i3的波形图。该实验结果进一步表明：

1)载波移相技术能基本消除高频谐波电流分量。

2)模块间的环流不流入并联后电网系统。

3)比较图9和图12中的电流i2和i3，OF能对高频电流分量中非环流分量起到抑制作用。

图12　载波移相时LC滤波器前和系统侧电流波形图Fig.12　Currents before the LC-filter and of the parallel system when modulated carrier waves asynchronous

3)谐波补偿实验

采用所提并联系统协调控制方法的谐波补偿实验波形如图13所示。由图可见，该协调控制方法能有效抑制ic中的高频开关谐波环流，装置对谐波具有较好的补偿效果。

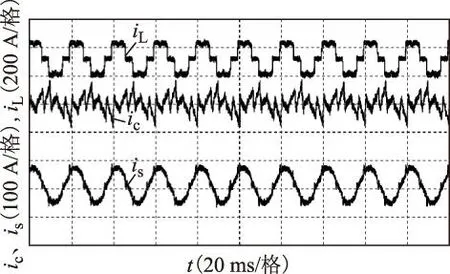
图13　谐波补偿实验图Fig.13　Experimental graphs of haimonic compensation

6结论

本文通过理论、仿真和实验分析，开展了对多模块APF并联系统的高频谐波环流形成机理及其影响、LC输出滤波器对高频环流的影响等方面的研究，并提出一种多模块APF协调控制方法以抑制高频谐波环流。研究结论表明：

1)高频环流的主要成因是各模块输出高频开关谐波电压存在偏差，而该偏差取决于各模块电路参数的一致性、直流侧电压的均衡性以及控制系统的同步性等诸多因素。

2)在各模块电路参数和直流侧电压一致以及调制波相同的理想条件下，高频谐波环流主要取决于各模块SPWM载波的同步性，当载波同步时高频环流为零。

3)载波移相可消除并联系统电流中Nωc以下的高频开关分量，同时会造成模块间的高频环流，但该环流只在模块间流动，不流入并联后电网系统。

4)各模块输出滤波器，对于高频谐波环流基本没有抑制作用，相反由于其谐振特性，会降低系统的稳定性。此外，LC型滤波器能有效抑制各模块输出高频电流中的非环流部分。

5)所提模块化APF并联系统协调控制方法可有效抑制系统的高频谐波环流。

参考文献

[1]Dang Pengpai，Ellinger T，Petzoldt J.Dynamic interaction analysis of APF systems[J].IEEE Transactions Industrial Electronics，2014，61(9)：4467-4473.

[2]Sun Xiaofeng，Zeng Jian，Chen Zhe.APF for harmonic voltage resonance suppression in distribution system[C]//2nd IEEE International Power Electronics for Distributed Generation Systems，Hefei，2010：818-822.

[3]Rahmani S，Hamadi A，Al-Haddad K，et al.A combination of shunt hybrid power filter and thyristor-controlled reactor for power quality[J].IEEE Transactions Industrial Electronics，2014，61(5)：2152-2164.

[4]Fang Hongjuan，Yang Rongfeng，Yu Yannan，et al.A study on the DC voltage control techniques of cascaded multilevel APF[C]//7th International Power Electronics and Motion Control Conference，Harbin，2012：2727-2731.

[5]Wang Yafang，Gu Juping，Chen Ruixiang，et al.The multi-modular shunt APF based on direct current control and frequency doubling carrier phase-shifted SPWM[C]//IEEE ECCE Asia Downunder，Melbourne，VIC，2013：867-871.

[6]Xie Chuan，Wang Yue，Zhong Xiaojian，et al.A novel active damping method for LCL-filter-based shunt Active Power Filter[C]//IEEE International Symposium on Industrial Electronics，Hangzhou，2012：64-69.

[7]Pan Donghua，Ruan Xinbo，Wang Xuehua，et al.Magnetic integration of an LCL filter for the single-phase grid-connected inverter[C]//IEEE Energy Conversion Congress and Exposition，Raleigh，NC，2012：573-578.

[8]Ilves K，Antonopoulos A，Harnefors L，et al.Circulating current control in modular multilevel converters with fundamental switching frequency[C]//2012 7th International Power Electronics and Motion Control Conference，Harbin，2012，1：249-256.

[9]Xu Fan，Guo Ben，Xu Zhuxian，et al.SiC based current source rectifier paralleling and circulating current suppression[C]//Twenty-Eighth Annual IEEE Applied Power Electronics Conference and Exposition，Long Beach，CA，2013：402-409.

[10]何国锋，徐德鸿.基于解耦控制的多模块逆变器并联系统直流环流抑制策略[J].中国电机工程学报，2012，32(18)：43-50.

He Guofeng，Xu Dehong.The DC circulation current control strategy based on decoupled control scheme in the multi-module paralleled inverter system[J].Proceedings of the CSEE，2012，32(18)：43-50.

[11]余蜜，康勇，张宇，等.基于环流阻抗的逆变器并联控制策略[J].中国电机工程学报，2008，28(18)：42-46.

Yu Mi，Kang Yong，Zhang Yu，et al.Research on a novel current-sharing scheme based on circulating impedance of multi-inverter parallel system[J].Proceedings of the CSEE，2008，28(18)：42-46.

[12]Khadem S K，Basu M，Conlon M F.Reduction of circulating current flow in parallel operation of APF based on hysteresis current control[C]//48th International Universities Power Engineering Conference，Dublin，2013：1-6.

[13]平定钢，孔洁，陈国柱.载波移相SPWM 并联变流器及其环流问题的研究[J].电气自动化，2008，30 (4)：17-19.

Ping Dinggang，Kong Jie，Chen Guozhu.The research on carrier phase-shift SPWM and circulation currents in parallel converters[J].Electrical Automation，2008，30(4)：17-19.

[14]杨晓利，葛宝明，姜新建.并联型多重化三相四线有源电力滤波器综合控制策略研究[J].电力系统保护与控制，2012，40(23)：103-108.

Yang Xiaoli，Ge Baoming，Jiang Xinjian.Integrated control strategy of three-phase four-wire shunt active power filter using multiple converters[J].Power System Protection and Control，2012，40(23)：103-108.

[15]杨波，曾光，钟彦儒，等.大容量链式多电平变换器的优化CPS-PWM方法[J].电工技术学报，2013，28(10)：167-178.

Yang Bo，Zeng Guang，Zhong Yanru，et al.An optimal CPS-PWM strateg for high-power cascaded multilevel converters[J].Transactions of China Electrotechnical Society，2013，28(10)：167-178.

[16]许胜，赵剑锋.基于不对称规则采样法的级联H桥型变流器CPS-SPWM输出电压谐波特性分析[J].电工技术学报，2011，26(6)：121-128.

Xu Sheng，Zhao Jianfeng.Analysis of the harmonic characteristics of the CPS-SPWM output voltage of cascaded H-bridge converters based on irregular sampling[J].Transactions of China Electrotechnical Society，2011，26(6)：121-128.

许胜男，1976年生，博士，副教授，研究方向为电力电子技术在电力系统中的应用。

E-mail：xush_00@sina.com(通信作者)

费树岷男，1961年生，教授，博士生导师，研究方向为非线性控制和模式识别等。

E-mail：smfei@seu.edu.cn

作者简介

中图分类号：TM46

收稿日期2015-01-22改稿日期2015-12-15

江苏省高校自然科学研究项目(14KJB470008)、江苏省产学研联合创新资金前瞻性联合研究项目(BY2014127-15)和江苏省“青蓝工程”基金资助。