基于120°坐标系的SVPWM算法研究
孙鹤旭 荆 锴 董 砚 郑 易
(1.河北工业大学控制科学与工程学院 风电系统控制与测试工程技术研究中心 天津 300130
2.河北科技大学 石家庄 050018)
基于120°坐标系的SVPWM算法研究
孙鹤旭1,2荆锴1董砚1郑易1
(1.河北工业大学控制科学与工程学院 风电系统控制与测试工程技术研究中心天津300130
2.河北科技大学石家庄050018)
摘要针对传统空间矢量脉宽调制(SVPWM)算法结构复杂及运算量大等问题,提出一种基于120° AB非正交坐标系的SVPWM算法。该算法首先打破直角坐标系的约束,选取互差120°的单位矢量为基,构建非正交坐标系,进而将空间矢量变换到该坐标系下,利用两个坐标分量进行扇区判断、作用时间运算以及产生PWM信号,实现了SVPWM算法。通过仿真和实验,验证了该SVPWM算法的正确性,并在数字控制器的算法实现上与传统算法进行对比,得出该算法具有结构简单、运算快速以及控制精确等优势。
关键词:空间矢量非正交坐标系脉宽调制扇区
Research of SVPWM Algorithm Based on 120° Coordinates System
SunHexu1,2JingKai1DongYan1ZhengYi1
(1.Engineering Technology Research Center of Wind Power System Control and Testing School of Control Science and EngineeringHebei University of TechnologyTianjin300130China2.Hebei University of Science and TechnologyShijiazhuang050018China)
AbstractA new space vector pulse width modulation (SVPWM) algorithm based on 120° AB non-orthogonal coordinates is put forward in order to avoid the problems of structure complexity and large computation of the traditional algorithm.The constraint of Cartesian coordinates system is broken and two unit vectors with 120° angle are used as the bases to compose the novel non-orthogonal coordinates.Then,each space vector can be transformed into this coordinates.Through the judgment and operation of both coordinate components,the sectors judgment,action time calculation,and PWM signal’s generation can be accomplished to implement the SVPWM algorithm.At last,simulations and experiments verify the correctness of the proposed algorithm.By comparing with the traditional algorithm in digital controllers,the simplicity,speediness,and exactness of the proposed SVPWM algorithm have been testified.
Keywords:Space vector,non-orthogonal coordinates system,PWM,sector
0引言
近年来,随着数字控制技术以及电力电子技术的快速发展,高性能的传动控制系统对其逆变电路的脉宽调制技术要求也越来越高,其中,空间矢量脉宽调制(Space Vector Pulse Width Modulation,SVPWM)技术因具有电压利用率高以及谐波损耗小等优点,已成为广泛应用的PWM技术之一。
SVPWM是以磁链跟踪控制为目标的调制技术,在矢量控制[1-3]的电流闭环内较为常用,以实现对电流的稳定控制;亦有将SVPWM用于直接转矩控制[4,5]以及宽调速范围的弱磁控制[6]等电机控制中。而传统的SVPWM算法结构较为复杂,在应用于数字控制时,对处理器的速度要求较高,很多学者对此进行了研究。文献[7]直接利用三相电压的大小排序和差值来判断扇区和计算作用时间。文献[8]省略了传统算法中的扇区选择,简化了运算。文献[9]根据SVPWM中对顶两扇区的计算规律,对算法进行简化,以降低算法的硬件资源消耗。然而上述方法仍是在传统SVPWM技术的基础上进行的优化改进,对算法结构的简化有限。文献[10]给出了基于abc坐标系的SVPWM调制技术,却未脱离传统调制技术的限制。文献[11]提出了无扇区SVPWM技术,在一定程度上简化了传统控制策略的复杂性。文献[12]对三电平逆变器的SVPWM采用60°非正交坐标系,对双电平逆变电路的PWM调制技术具有非常重要的借鉴意义。
传统SVPWM算法以α-β坐标系为基础,在数字控制器中实现的复杂性主要体现在以下两点:①坐标变换及参考量等计算中,较多浮点型参数运算会大大增加控制器的运算量;②计算扇区和计算开关管作用时间的过程繁琐,两次以上的判断和运算,也使得算法更加复杂。
本文提出一种120° AB坐标系下的SVPWM算法,首先以a、b两相轴线构建120°非正交坐标系,并对该坐标系中矢量表示的惟一性进行论证;其次研究并提出该坐标系下包含坐标变换、扇区划分、作用时间计算及PWM波调制等过程的SVPWM算法;最后通过仿真和实验对本文算法进行验证,并从算法结构、执行时间以及控制效果上与传统算法进行对比分析,以验证本文算法的调制性能。
1120° AB坐标系的提出及坐标变换
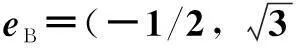
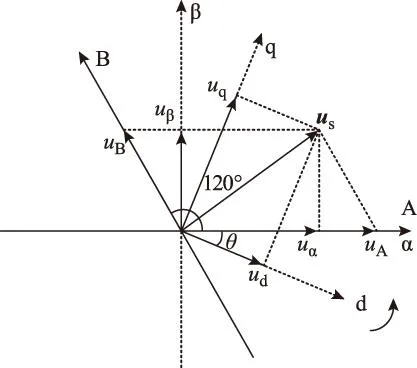
图1 空间矢量坐标变换示意图Fig.1 Coordinates transformation for space vector

空间矢量us在不同坐标系下具有不同的坐标描述,它们之间的变换可通过非奇异过渡矩阵实现。本文所提出的非正交120° AB坐标系与通用的α-β静止坐标系、d-q同步旋转坐标系以及三相坐标之间的矢量分解关系在图1中给出,其正逆变换关系如式(1)~式(3)所示。
(1)
(2)
(3)
式中,u0=0,与传统的“3/2变换”类似,是人为增加的零轴分量。
采用本文提出的120° AB坐标系代替传统的α-β坐标系,将为SVPWM算法在数字控制器上的快速实现提供十分便易的前提条件。
2120° AB坐标系下的SVPWM算法
SVPWM采用“伏秒等效”原则,电压矢量us的作用可等效为几个由逆变器产生的基础电压矢量Ui分别作用一段时间Ti所产生的效果的总和
(4)
式中,ui为us在基本电压矢量Ui方向上的投影;“=”既表示空间矢量合成关系的相等,又表示在控制周期上产生等效的作用。于是SVPWM的调制目标即选择合适的基本电压矢量,合理配置开关管开通的占空比,以达到所需电压矢量的效果。另外,若考虑逆变器开关损耗,需对输出的PWM信号形式做进一步调整。
2.1基础电压矢量及120° AB坐标系下的扇区划分
本文选取的基础电压矢量:三相逆变器某一相状态为“1”(上闭下开),则输出该相的有效电压矢量Ux(x=a,b,c),该电压矢量幅值为2Udc/3,方向同该相轴线方向,在120° AB坐标系下,Ua(2Udc/3,0)与A轴平行,Ub(0,2Udc/3)与B轴平行,Uc(-2Udc/3,-2Udc/3)。若状态为“0”(上开下闭),则输出零电压矢量0。各相的状态相互独立,作用于负载的电压满足叠加原理,在空间矢量上也满足矢量合成关系。比如a相为“1”,b、c相均为“0”时,输出电压为Ua;若a、b相均为“1”,c相为“0”时,输出则为Ua+Ub,方向与120° AB坐标系第一象限的角平分线方向重合,幅值为2Udc/3,与基础电压矢量相同;若a、b、c相均为“1”,输出则为Ua+Ub+Uc=0。
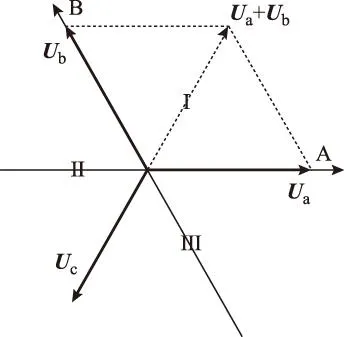
图2 扇区分割示意图Fig.2 Sectors segmentation
整个空间平面被Ua、Ub、Uc分成3个顶角120°的扇形区域,相比于传统60°的扇区划分(小扇区),这里称之为大扇区,并记作Ⅰ、Ⅱ、Ⅲ。于是,一个大扇区包含两个小扇区。根据空间矢量us在120° AB坐标系下的坐标uA、uB,扇区的判断过程被简化。取变量X=uA,Y=-uB,Z=uB-uA,大扇区的判别方式见表1。

表1 扇区判断
如果取N=0、1、2对应Ⅰ、Ⅱ、Ⅲ,由逻辑运算
N=
2int[(Y>0)∧(Z<0)]+int[(Z>0)∧(X<0)]
(5)
式中,int[·]表示在数字控制器中将任意数据类型强制转换为整型,这里即将判断的逻辑1转换为整型数1,逻辑0转换为整型数0。
此外,在本文所提坐标系下,传统扇区(小扇区)的判断方法也得到了简化,在大扇区判断条件的基础上,增加附加条件的判断,即可得到最小扇区的编号,见表1。传统算法中3个判断变量X、Y、Z的计算存在大量的浮点数运算,判断结果需要一次计算再加一次变换才能得到实际的扇区序号。相比于传统算法,本文120° AB坐标系下的扇区判断方法得到了较大简化。
2.2120° AB坐标系下作用时间的计算
扇区的划分目的在于选取最少的电压矢量来表征us的作用。在大扇区的划分下,将us分解成沿所在扇区两边方向的两个电压矢量的合成,在所剩余一相基础电压矢量方向上的分解为0,则分解所得到的电压矢量的幅值,均可由us在120° AB坐标上的坐标值得到的变量X、Y、Z表示,如表2所示。
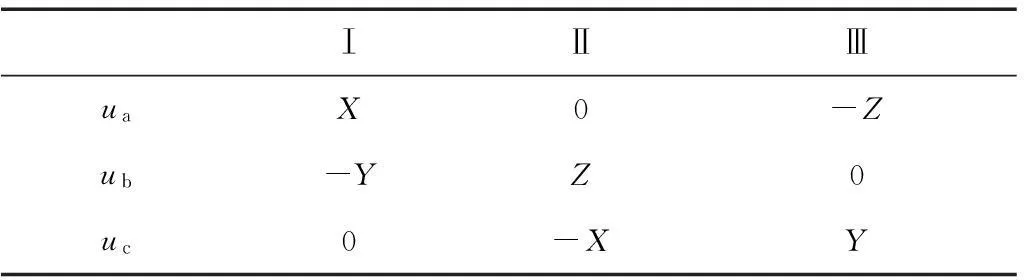
表2 大扇区ua、ub、uc的计算
表2中ua、ub、uc分别为在3个基本矢量Ua、Ub、Uc方向上分解矢量的幅值。依照式(4),分解矢量可等效为基本电压矢量在控制周期Ts内一段时间Ti上的作用,在这里取i=a,b,c。于是基础电压矢量的作用时间Ti(Ti≤Ts)可表示为
(6)
另外,传统SVPWM方法在计算时间上存在较多的浮点运算,对于数字控制器而言,需要占用大量运算时间。而在本文所提坐标系下,传统扇区(小扇区)矢量分解中的6个有效电压矢量和2个零电压矢量作用时间的计算也得到了简化。表3中给出了传统扇区(小扇区)按逆时针顺序的两个分解矢量u1和u2幅值的计算。
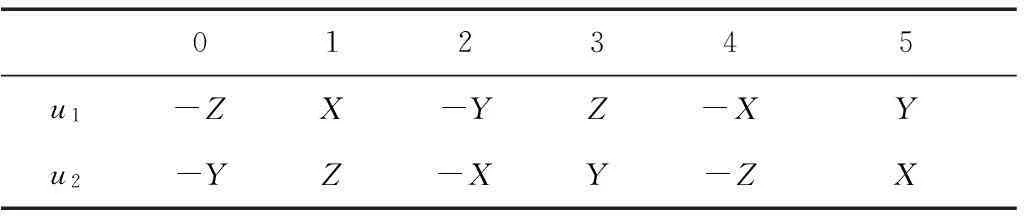
表3 小扇区u1、u2的计算
有效电压矢量的计算同式(6),其中i=1,2,零电压矢量作用时间T0=Ts-T1-T2。
进一步,作用时间的计算中还必须考虑基础矢量作用时间的约束问题,即有效电压矢量作用时间的最大值Tmax不得超过控制周期Ts。对于本文所提的大扇区划分模式以及传统小扇区划分模式有
大扇区模式:Tmax=max{Ta,Tb,Tc}≤Ts
(7)
小扇区模式:Tmax=T1+T2≤Ts
(8)
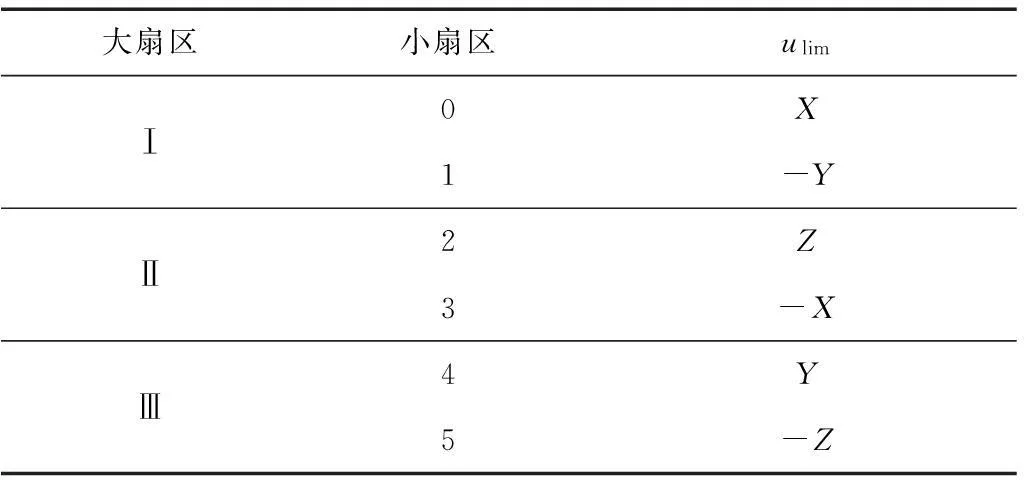
表4 不同扇区的上限电压umax
从表4中也可看出大、小扇区模式下的umax一致,比如Ⅰ扇区umax=max{X,-Y, 0},而与之相对应的0、1小扇区判断条件umax=u1+u2,分别为-Z-Y=X和X+Z=-Y,即max{ua,ub,uc}=u1+u2。于是统一的含有约束条件的作用时间计算公式为
(9)
式中,i为大扇区模式下的a、b、c或小扇区模式下的1、2。则进行包含约束条件的调制时,大扇区模式下也需要参考所在小扇区的约束条件。
通常对于DSP等通过定时/计数器实现PWM周期的输出,这里的Ts可直接利用定时/计数器的计数周期来代替,输出将变为计数器的数值比较值。
2.3PWM波的调制
对于大扇区模式下的基础矢量,由于相互独立,作用时间可任意叠加。但考虑减小开关器件的损耗,通常采用5段或7段式的PWM方式[13],如图3所示。
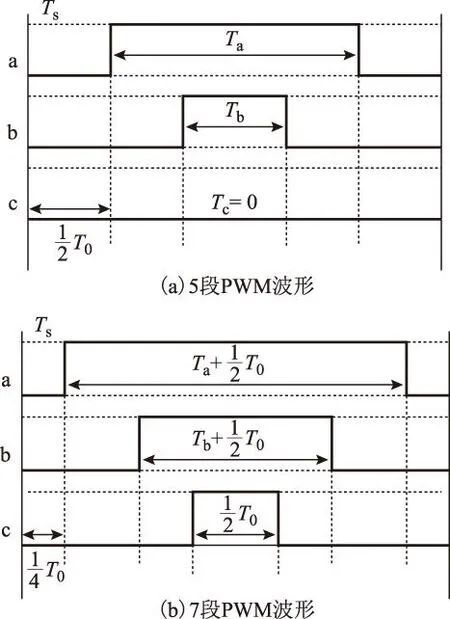
图3 两种PWM波形Fig.3 Two kinds of PWM waveform
利用以Ts为周期的增减计数器,与计算得到的各相作用时间单独比较,即可调制出各相上桥臂开关管的PWM控制波形,即5段式的波形。对于7段式的PWM,比较所用的作用时间需加上零矢量作用时间T0的1/2,其中T0=Ts-max{Ta,Tb,Tc}。上下桥臂波形互反,但切换时需保留一段死区时间[14],以保证开关管不会同时导通而导致短路。
对于小扇区模式,得到T1和T2后,要获得对称式的PWM波还需进一步计算和选择,这比大扇区模式计算略显复杂,调制方式与传统PWM相同。但对于一些含有SVPWM功能的控制芯片(如24系列、28系列的DSP),在选择了扇区以及矢量给定顺序后,则可直接将T1和T2对应的比较值给到相应比较寄存器CMPRx中,得到DSP所带的一种5段PWM波。
由此,基于120° AB坐标系的SVPWM算法得以实现,其算法流程框图如图4所示。
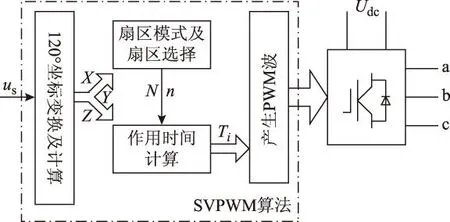
图4 120° AB坐标下的SVPWM算法框图Fig.4 Block diagram for SVPWM on 120° AB coordinate
本文算法相比传统算法计算步骤得到简化,既避免了浮点数在数字控制器运算中的严重耗时,又减少了浮点数处理过程的舍入误差,大大提高了运算速度及可调制准确度,使SVPWM在数字控制器中更易实现。
3算法仿真及实验
3.1算法仿真
在Matlab/Simulink环境下搭建SVPWM算法模块以及逆变电路,仿真条件:同步控制周期Ts为100 μs,直流母线电压Udc为311 V,开关器件的开关频率为10 kHz。仿真以幅值恒定的旋转空间电压矢量的调制为例,对本文算法进行验证,设定空间电压矢量us在静止坐标系下的同步转速为3 000 r/min,幅值为100 V,方向为逆时针方向,对应于调制出的三相交流电压的最大值100 V,频率为50 Hz。仿真的调制方法采用大扇区模式,计算较为简单。
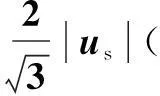

图5 变换坐标uA、uB波形Fig.5 Waveforms of the components uA、uB
以α轴为0°起始,uA的峰值出现在电压矢量us的30°相位处,谷值出现在210°处,而uB的峰值和谷值分别对应电压矢量us在90°和270°位置。根据坐标变换得到的uA和uB依本文方法进行扇区选择,如图6所示。
图6中同时示出了本文扇区分割方法的大、小扇区序号,一个大扇区对应两个小扇区,对于大扇区0、1、2分别对应于扇区编号Ⅰ、Ⅱ、Ⅲ,小扇区的数值即为扇区编号0~5。仿真采用大扇区模式,由uA和uB的大小以及其所对应的大扇区可计算出a、b、c三路上桥臂导通的作用时间Ta、Tb、Tc,作用时间随时间的变化规律如图7所示。
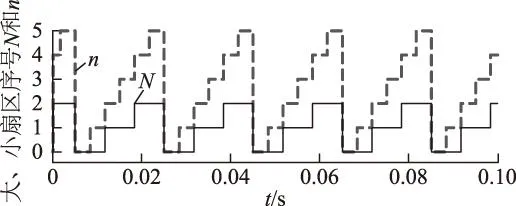
图6 大、小扇区判断波形Fig.6 Waveforms for sectors judgment

图7 大扇区模式下作用时间波形Fig.7 Action times for large-sector-mode
按5段方式调制,图7中虚线t1和t2时刻处的PWM波形如图8所示,波形为对称形式,图8a为t1时刻附近3个周期的三相PWM波形,正位于b、c两相作用时间切换的位置,其中a相PWM信号的占空比约为55%,b相占空比从0逐渐增加,c相由1%减小到0。图8b为t2时刻附近3个周期的PWM波形,t2时刻a、b两相的作用时间几近相等,占空比约为55%,c相上桥臂开通时间tc为0,图中PWM信号占空比为0。
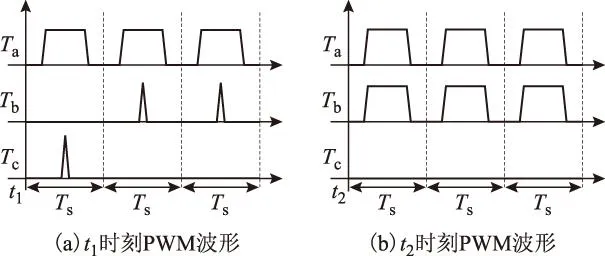
图8 t1、t2时刻的PWM波形Fig.8 PWM waveforms on t1 and t2
在所调制出的PWM信号作用下,桥式逆变器输出的线电压波形和相电压波形如图9所示。
线电压最大值为直流母线电压311 V,相电压最大值约为220 V。经过RC低通滤波器后,线电压和相电压波形如图 10所示。滤波后线电压与相电压的波形十分接近正弦波,线电压峰值约为175 V,相电压峰值约为101 V。

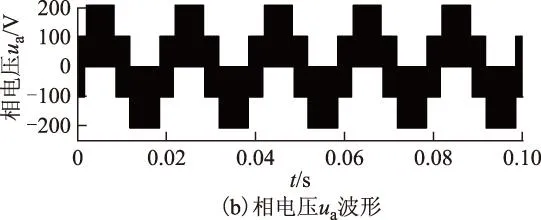
图9 输出的调制电压波形Fig.9 The modulation voltage waveform

图10 经低通滤波后的调制电压波形Fig.10 The waveforms of modulation voltage after low-pass filtering
此外,在Matlab环境下对本文SVPWM算法和传统SVPWM算法的运行时间进行对比,采用1 000次的循环运算,并多次实验取平均,可得传统SVPWM算法耗时35.84 ms,而本文算法耗时29.96 ms,较传统算法用时减少了16.4%,提高了SVPWM的运算速率。
3.2实验
实验平台采用基于TMS320F2407为核心的DSP控制器,逆变部分采用智能功率模块PM15RSH120实现。实验平台由单相220 V市电供电,整流后得到的直流母线电压为309 V。控制周期与仿真相同,为100 μs,开关频率10 kHz。调制实验目标和仿真相同,按本文方法进行调制,输出电压由波形记录仪观测。
图11a为逆变器a、b两相输出端测得的线电压波形,周期0.02 s,即50 Hz。电压周期内,正负半周均由若干窄脉冲构成,幅值同直流母线电压。利用波形记录仪所带500 Hz低通滤波器对线电压进行滤波,得到图11b的正弦波波形,幅值约为170 V。直接测量线电压有效值为120.07 V,即对应幅值为169.80 V,折算到相电压幅值为98.04 V,与目标100 V非常接近,相对误差2%。
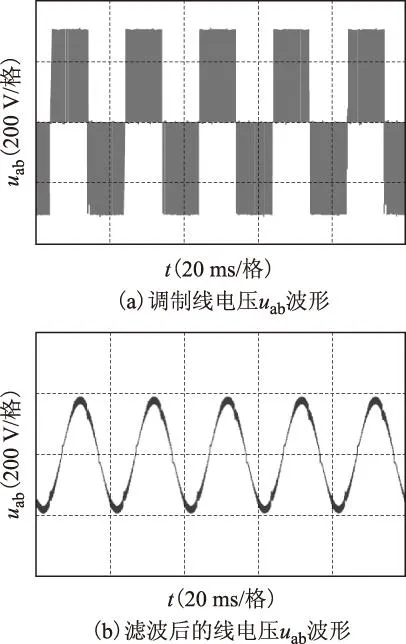
图11 实际输出的调制电压波形Fig.11 The actual waveforms of modulation voltage
另外,还对本文算法与传统算法在DSP中的实现进行了对比,其中,对程序中所有浮点运算都通过扩大倍数等方法进行整型化处理。执行时间如图12所示,一个控制周期100 μs内,本文算法需要时间约13.2 μs,而传统算法需要16.4 μs,本文算法的计算时间较传统算法缩短约20%。
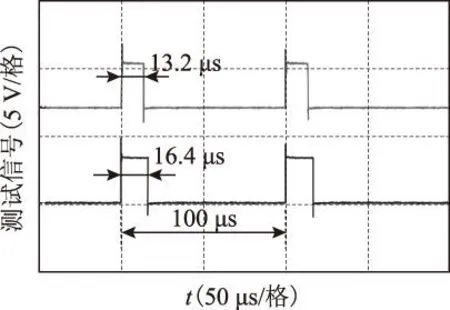
图12 算法时间对比Fig.12 Comparison of the execution time
两种算法的调制电压圆如图13所示,在DSP运算中,传统算法的电压圆发生了明显的畸变,而本文算法的电压圆能很好地跟随给定电压圆,调制更为精确。
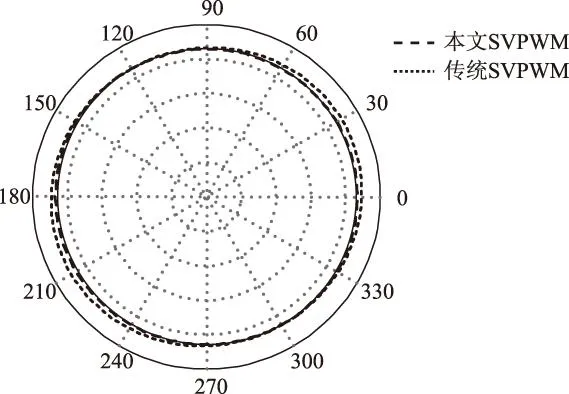
图13 SVPWM电压圆对比Fig.13 Comparison of the voltage circles
4结论
本文提出了一种建立在非正交坐标系下的SVPWM算法。通过建立120° AB非正交坐标系,简化了空间矢量变换以及运算过程;并基于该坐标系,详细描述了具有两种扇区模式的SVPWM算法流程,实现了对逆变器PWM控制信号的调制。仿真及实验结果表明,本文算法实现了空间电压矢量的调制,达到了预期的效果。此外,通过对算法结构、执行时间以及控制效果等与传统算法的对比分析,得出本文算法具有过程简洁、运算快速及调制精确等优势,在数字控制器中实现时,可缩短控制周期,提高电压调制准确度,具有很高的工程应用价值。
参考文献
[1]陈俊硕,刘景林,张颖.永磁同步电机新型矢量控制[J].西安电子科技大学学报(自然科学版),2014,41(4):179-185.
Chen Junshuo,Liu Jinglin,Zhang Ying.New vector control of the permanent magnet synchronous motor[J].Journal of Xidian University,2014,41(4):179-185.
[2]Michael P A,De Varajan N,Praveen K V.Indirect vector control of induction motor using space vector pulse-width-modulation (SVPWM)[J].Modelling,Measurement and Control A,2011,84(1-2):1-20.
[3]刘婷婷,谭彧,吴刚,等.基于SVPWM的高转速永磁同步电机控制系统的研究[J].电力系统保护与控制,2009,37(12):11-14.
Liu Tingting,Tan Yu,Wu Gang,et al.Simulating of high speed PMSM control system based on SVPWM[J].Power System Protection and Control,2009,37(12):11-14.
[4]Zhang Zhifeng,Tang Renyuan,Bai Baodong,et al.Novel direct torque control based on space vector modulation with adaptive stator flux observer for induction motors[J].IEEE Transactions on Magnetics,2010,46(8):3133-3136.
[5]曹承志,时洪图,尹明军.基于SVPWM 的直接转矩控制新方案[J].系统仿真学报,2008,20(21):5924-5928.
Cao Chengzhi,Shi Hongtu,Yin Mingjun,et al.Novel DTC system based on space vector pulse width modulation[J].Journal of System Simulation,2008,20(21):5924-5928.
[6]何亚屏,文宇良,许峻峰,等.基于多模式SVPWM 算法的永磁同步牵引电机弱磁控制策略[J].电工技术学报,2012,27(3):92-99.
He Yaping,Wen Yuliang,Xu Junfeng,et al.High-power permanent magnet fiux-weakening strategy based on multi-mode SVPWM[J].Transactions of China Electrotechnical Society,2012,27(3):92-99.
[7]张寅孩,汪松松,葛金法,等.一种新的差值SVPWM调制方法[J].电工技术学报,2010,25(8):99-104.
Zhang Yinhai,Wang Songsong,Ge Jinfa,et al.A novel SVPWM modulation method[J].Transactions of China Electrotechnical Society,2010,25(8):99-104.
[8]Zhu Rongwu,Wu Xiaojie.Simplified SVPWM that integrates overmodulation and neutral point potential control[J].Journal of Power Electronics,2014,14(5):926-936.
[9]齐昕,王冲,周晓敏,等.一种低硬件资源消耗快速SVPWM 算法[J].电机与控制学报,2014,18(4):31-38.
Qi Xin,Wang Chong,Zhou Xiaomin,et al.Low hardware resource consumption fast SVPWM algorithm[J].Electric Machines and Control,2014,18(4):31-38.
[10]邱银锋,梁志珊.abc坐标系下空间矢量PWM实现研究[J].电力系统保护与控制,2011,39(13):36-40.
Qiu Yinfeng,Liang Zhishan.Research on implementation of the space vector PWM in abc coordinates[J].Power System Protection and Control,2011,39(13):36-40.
[11]方斯琛,李丹,周波,等.新型无扇区空间矢量脉宽调制算法[J].中国电机工程学报,2008,28(30):35-40.
Fang Sichen,Li Dan,Zhou Bo,et al.A novel algorithm of space-vector PWM without sector calculation[J].Proceedings of the CSEE,2008,28(30):35-40.
[12]Lima E F F,Filho N P,Pinto J O P.FPGA implementation of space vector PWM algorithm for multilevel inverters using non-orthogonal moving reference frame[C]//IEEE International Electric Machines and Drives Conference,Miami,FL,2009:709-716.
[13]阎治安,唐明,易萍虎.电机控制中电压空间矢量脉宽调制算法的探究[J].西安交通大学学报,2006,40(12):1374-1377.
Yan Zhian,Tang Ming,Yi Pinghu.Space vector pulse width modulation algorithm with applications[J].Journal of Xi’an Jiaotong University,2006,40(12):1374-1377.
[14]黄招彬,游林儒,汪兆栋.一种考虑死区与最小脉宽限制的IPWM算法[J].电工技术学报,2014,29(12):12-18.
Huang Zhaobin,You Linru,Wang Zhaodong.A novel integrated pwm strategy considering dead-time and minimum pulse-width limitation[J].Transactions of China Electrotechnical Society,2014,29(12):12-18.
孙鹤旭男,1956年生,教授,博士生导师,研究方向为运动控制、工程系统与控制。
E-mail:hxsun@hebust.edu.cn
荆锴男,1987年生,博士研究生,研究方向为电机系统及其控制。
E-mail:jingkai_1082@126.com(通信作者)
作者简介
中图分类号:TM343
收稿日期2015-01-29改稿日期2015-12-15
河北省重大科技成果转化项目(13041709Z)、河北省自然科学基金(E2013202108)和河北省发改委项目(2013)资助。

