《三角形的内角和》教学设计

张晓刚（特级教师）

【教学内容】

人教版四年级下册第67页。

【教学目标】

1.学生自主动手量、拼、剪，发现、推理得出三角形的内角和是180°，并会用这一知识解决生活中的简单问题。

2.学生在思考和动手过程中，培养学生的创新意识和实践能力，渗透转化的思想。

【教学重点】

探索和发现三角形内角和等于180°。

【教学难点】

充分发挥主体作用，自主探索和发现三角形三个内角的度数和等于180°。

【教学过程】

一、复习旧知，引入问题

1.通过整理学具，发现直角三角形内角和与长方形内角和之间的关系。

师：同学们，你们手里有锐角三角形、钝角三角形，缺少了直角三角形怎么办，想想看？能用手中长方形的纸变出直角三角形吗？

预设一：学生从长方形上可能剪下一个角，得到一个直角三角形。

预设二：学生通过对折，得到两个相同的直角三角形。

师：我们已知了长方形有四个直角，所以它的内角和是360°，那么在这个基础上大家思考一下，和长方形有关系的这两个直角三角形的内角和是多少？你能不能猜出来呢？

【设计意图：教师在这里埋下了一个伏笔，既然长方形可以折成两个直角三角形，长方形的每个角都是直角，内角和为 90°×4=360°，那么推理出直角三角形的内角和等于180°也就是非常容易的事情了。直角三角形的内角和等于180°，那钝角、锐角三角形的直角和是不是也是180°呢？】

2.依据直角三角形的内角和猜一猜锐角三角形和钝角三角形内角和可能是多少？

师：刚才大家通过动手，把长方形平均分成两个相同的直角三角形，并且得出直角三角形的内角和等于180°，那钝角、锐角三角形的内角和可能是多少呢？你猜一猜，和小组同学商量一下，看看用什么方法可以求得？

预设一：锐角三角形内角和小于180°。

预设二：钝角三角形内角和大于180°。

预设三：所有三角形内角和都是180°。

【设计意图：分组讨论，是为了让学生解决问题有思路，有的同学可能会猜想，锐角三角形和钝角三角形的内角和比直角三角形的大一些、小一些或者相等，也可能有学生会拿出量角器，提出用“量一量”的方法验证，还有的学生可能会想到是不是可以折。在小组探究出可行性的方案后，下一步就可以组织学生分组行动研究了。】

二、自主探究，得出规律

1.分组动手测量，观察算式，猜想、推理。

师：大家分组测量一下你们小组的三角形，完成下表。_

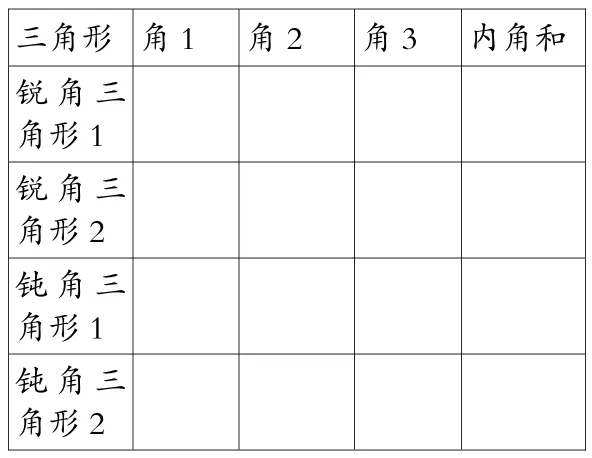
三角形_角1____角2_________________角3内角和锐角三角形1锐角三角形2钝角三角形1钝角三角形2____________________________

【设计意图：学生分组讨论，有学生利用刚才小组讨论的方法，会用“量一量”的方法，于是，大家纷纷动手开始量，并且把结果写出来。可能会写出这样的一些算式，比如：40+75+65=180 ，125°+25°+31°=181°等等。通过板书一对比，问题就出来了，有的学生书写不规范，没写角的度数符号“°”，有的学生量出来的不是180°，教师帮助学生分析原因：一是我们手中的量角器并不精确；二是学生可能在测量时我们估计了一部分，所以结果会出现误差。】

2.分组动手“拼一拼”的活动，进一步观察、思考和推理。

师：我们发现，测量出的这些三角形的内角和有的大一些，有的小一些，但是这些三角形内角和的数值基本都在180°附近，那大家想一想180°的角是一个什么样的角？再想想三角形的三个角，和这个180°的角之间有什么样的关系，你又可以通过动手发现什么？

预设一：学生知道180°是一个平角，可以剪下两个和另外一个拼。

预设二：学生知道180°是一个平角，可以剪下三个角去拼。

预设三：也许有个别小组会用折的方法，沿中位线对折，把三个角拼成一个平角。

【设计意图：在经历了“量一量”之后，教师继续引导学生思考这个180°的平角和三角形的三个内角之间的关系，从而为拼角找到思路。活动中可能有学生说可以“拼一拼”，那么如何拼？学生可能会说把其中两个角剪掉然后拼在一起，也有性急的学生拿出剪刀来直接就剪了。这个时候，教师还要提醒小组研究的时候注意，我们是不是应该把现有三角形的三个角分别标记∠1、∠2、∠3呀，要不然待会剪完了，那么多角，你能知道哪个是原来三角形的吗？这个环节要充分调动学生的主动性思维，分析推理的可能性，通过小组的动手完成对刚才推理的验证。】

3.利用活动经验深度思考，再次动手验证规律。

师：同学们，看看教材67页“做一做”的2，大家动手做一做，想一想。

预设：学生剪开后看是两个直角三角形，知道内角和是180°。

师：做完之后再把这两个三角形合起来，再想一想，你又有什么新的发现。对于任意的三角形，我们还可以怎么研究它的内角和呢？

预设：这个环节比较抽象，可能大部分学生猜不出来它们之间的关系。

师：我们动手平移，你发现了这两个三角形的两条直角边怎么样了？变成了这个新的大三角形的什么？

【设计意图：这个练习很有思考的价值，把一个任意的三角形沿着高剪开，形成两个直角三角形，每个三角形的内角和依旧是180°。那么逆向思考，有像这样的两个直角三角形，也可以合成一个三角形，它的内角和又是多少度呢？从而对三角形内角和的探究更深一个层次，对前两次的探究有了更加深刻的理解，进一步理解了三角形内角和180°的含义，从而体会出三角形的内角和与三角形的大小无关。】

三、检测练习

1.判断题。

（1）一个三角形三个角的度数分别是80°、75°、24°。

（2）一个三角形中最多有一个钝角。

（3）三角形越大，它的内角和就越大。

2.考考你。

在一个三角形中，∠1=140°，∠3=25°，求：∠2=？

3.做一做。

（1）有一个三角形，已知一个角是30°，另外两个角的和是多少？

（2）有一个直角三角形，已知一个角是3°，另外两个角的和是多少？

（3）有一个直角三角形，剪去任意一个角，剩余图形的内角和可能是多少？

【设计意图：判断题的这三道题其实是从“三角形内角和的度数、钝角的数量，三角形的面积和内角和的关系”三个不同的侧面来出题，进一步让学生巩固新知，在“考考你”环节，题目是“在一个三角形中，∠1=140°，∠3=25°，求：∠2的度数？”继续在巩固新知。在“做一做”环节，题目的角度在不断变换，难度逐步加深，第（1）题“有一个三角形，已知一个角是30°，另外两个角的和是多少？”这里答案有多种；第（2）题只将“有一个三角形”改成“有一个直角三角形”，条件一变，答案随之就只有一种了；第（3）题“有一个直角三角形，已知一个角是30°，剪去这个角，剩余图形的内角和是多少？这个题目有两种可能，学生可能考虑不周全。】

四、反思小结

师：这节课你学会了什么？怎么学会的？你有什么意外的收获吗？这节课你还觉得有什么不足？这节课你想给老师提什么样的建议？