基于三角白化权函数的装备维修合同商服务质量评估

王双川， 吕瑞强， 胡恩勇， 杨 阳

(1. 空军勤务学院航空四站系， 江苏 徐州 221000； 2. 空军勤务学院训练部， 江苏 徐州 221000)

基于三角白化权函数的装备维修合同商服务质量评估

王双川1， 吕瑞强1， 胡恩勇2， 杨 阳1

(1. 空军勤务学院航空四站系， 江苏 徐州 221000； 2. 空军勤务学院训练部， 江苏 徐州 221000)

针对合同交付阶段装备维修合同商服务质量的评价问题，建立了装备维修合同商服务质量评价指标体系，运用模糊层次分析法(Fuzzy Analytical Hierarchy Process，FAHP)确定了各级指标权重，构建了基于中心点三角白化权函数的装备维修合同商服务质量评价模型，并通过算例验证了该模型的适用性和有效性。

模糊层次分析法； 三角白化权函数； 装备维修合同商； 服务质量评估

合同商保障是军民融合保障的主要模式之一，其实质是把军队部分保障工作以合同的形式交给地方企业，以充分利用民间丰富的物质、技术和人力等资源来增强军队的保障能力[1]。李环林[2]、杨华等[3]将装备维修合同商保障大致分为合同准备、合同订立、合同履行和合同交付4个阶段，其中：合同商服务质量评价是合同交付阶段的主要活动之一。装备维修合同商服务质量评价是从多角度、多层次对整个合同商保障过程的服务质量满足规定要求的程度进行判定，其目的是对整个合同的完成情况进行评价，查找分析合同成功或失败的原因、总结经验教训，并决定合同的续签或终止等。

目前，装备维修合同商保障研究主要集中在装备维修合同商的选择与评价以及合同商保障风险的识别与评估等方面[3-7]，有关装备维修合同商服务质量评价方面的研究较少[8-9]。由于装备维修合同商保障内容较多，保障过程中涉及的相关因素复杂，各相关因素对服务质量的影响既有定性的也有定量的，很难直接比较主次，且各评估指标之间呈现出交叉性和非线性等特点；另一方面，由于评估指标体系中各指标的量纲不同，装备维修合同商服务质量评估呈现出灰色性和偶然性等特点[10]。传统的服务质量评估方法，如层次分析法、SERVQUAL(Service Quality)量表评价法[11]、关键事件法[12]、模糊综合评判法[8]、顾客满意度指数法等，虽然简单、方便，但由于忽略了评估过程的模糊性和灰色性，导致许多有用信息丢失，难以全面综合地度量各项评估指标，并对服务质量作出准确评价。基于模糊层次分析法(Fuzzy Analytical Hierarchy Process，FAHP)和中心点三角白化权函数的灰色聚类评估方法能较好地解决上述问题，该方法通过FAHP法充分利用了定性指标的模糊信息，解决了信息丢失问题，提高了信息利用率；其通过中心点三角白化权函数模型解决了评估指标的灰色性和不确定性问题，使装备维修合同商服务质量的评价更加科学、合理。

1 装备维修合同商服务质量评价指标体系

装备维修工作的复杂性决定了装备维修合同商保障服务的过程不是一个简单的流程，而是一个多环节、多层次的系统工程。笔者根据GJB/Z3—88《军工产品售后技术服务》要求及装备维修合同商保障特点，对影响合同商服务质量的各种要素进行分析，并结合相关文献资料和专家经验，采用层次分析法建立了装备维修合同商服务质量评价指标体系，如表1所示。其中：“装备维修合同商服务质量”为评估总目标；有效性、规范性、安全性、主动性、响应性和部队满意度为一级指标，表征服务质量应考虑的6个方面，6个方面依次展开即为二级指标。

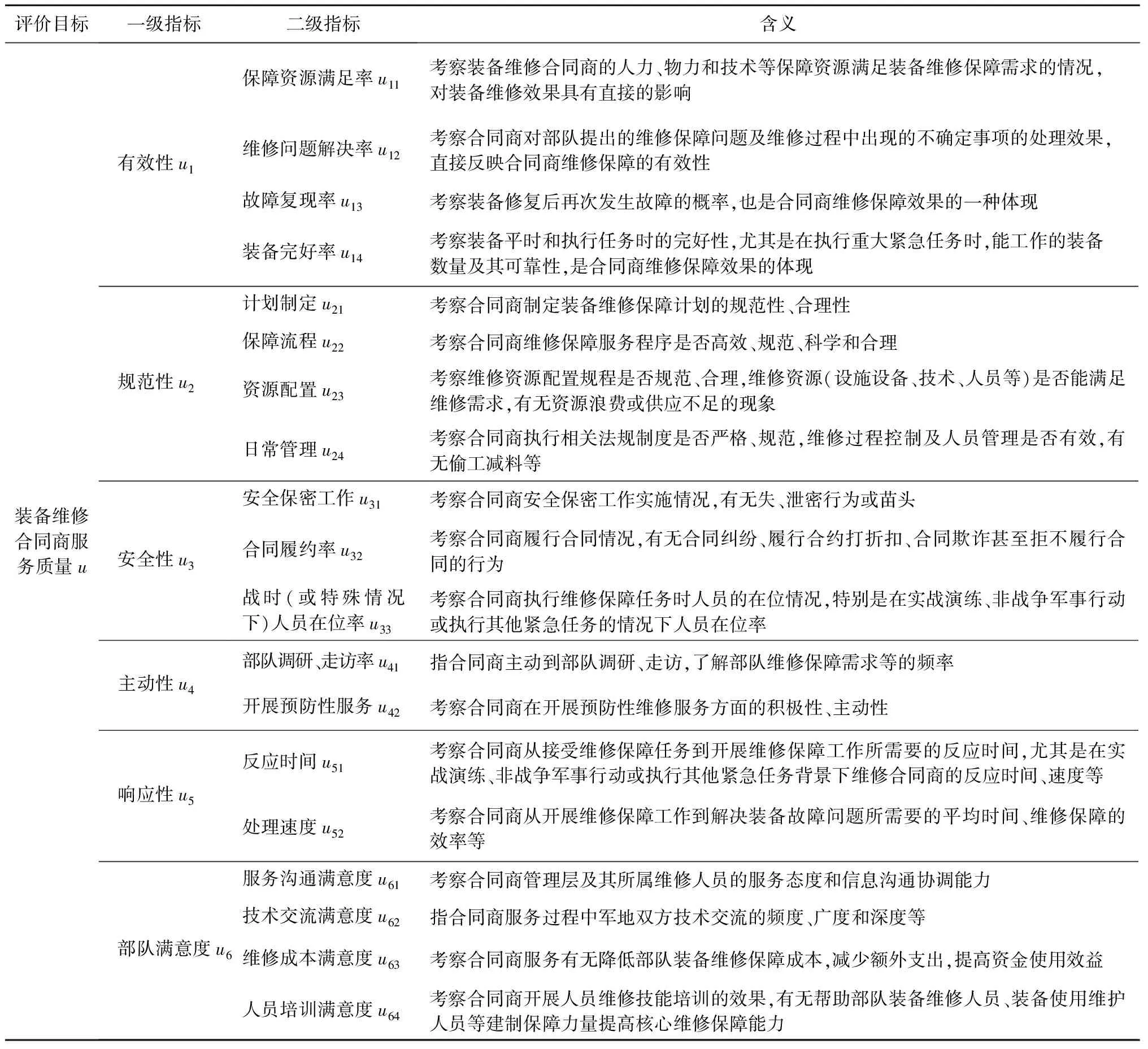
表1 装备维修合同商服务质量评价指标体系

2 基于FAHP和中心点三角白化权函数的评价模型

2.1 FAHP求解指标权重的步骤

FAHP[13]是一种将定性分析、定量分析和模糊评判相结合的系统分析方法，应用该方法求解装备维修合同商服务质量评价指标权重的具体步骤如下：

1)建立模糊互补判断矩阵。设a1,a2,…,aq为元素B对应的下一层元素，phl(h，l=1,2，…,q)为元素ah和al相对于元素B进行比较时的相对重要度关系。为了确定元素ah相对于al的相对重要度关系，建立0.1～0.9的模糊判断尺度，如表2所示。

表2 0.1～0.9模糊判断尺度

由此可得各级评价指标的模糊互补判断矩阵P=(phl)q×q。

2)构造模糊一致判断矩阵。将模糊互补判断矩阵P改造成模糊一致判断矩阵R=(rhl)q×q，其中：

rhl=(rh-rl)/[2(q-1)]+0.5，

(1)

(2)

3)计算指标权重。对R的每行元素进行求和，并进行归一化处理，即可得到各项指标相对于上层指标的权重，即

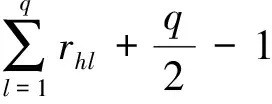
(3)

2.2 基于中心点三角白化权函数的评价模型

设有n个被评价对象、s个灰类，xij为被评价对象i(i=1,2,…,n)的第j(j=1,2,…,m)个评价指标的观察值，则基于中心点三角百化权函数评价模型进行评价的具体步骤如下[14-15]：

1)根据评价要求划分灰类数s，确定各灰类的中心点(最可能属于某一灰类的点，该点不一定与小区间的中心点相对应)λ1,λ2,…,λs，并将各指标的取值范围也相应地划分为s个区间。

2)第1个灰类和第s个灰类分别向左、右2个方向延拓，则增加第0个灰类和第s+1个灰类，其中心点分别为λ0,λs+1，则得到新中心点序列为λ0,λ1,λ2,…,λs,λs+1；然后将点(λk,1)与第k-1和k+1个小灰类的中心点(λk-1,0)和(λk+1,0)相连接，即可得到指标j关于灰类k的中心点三角白化权函数fjk(·)，k=1,2,…,s，如图1所示。

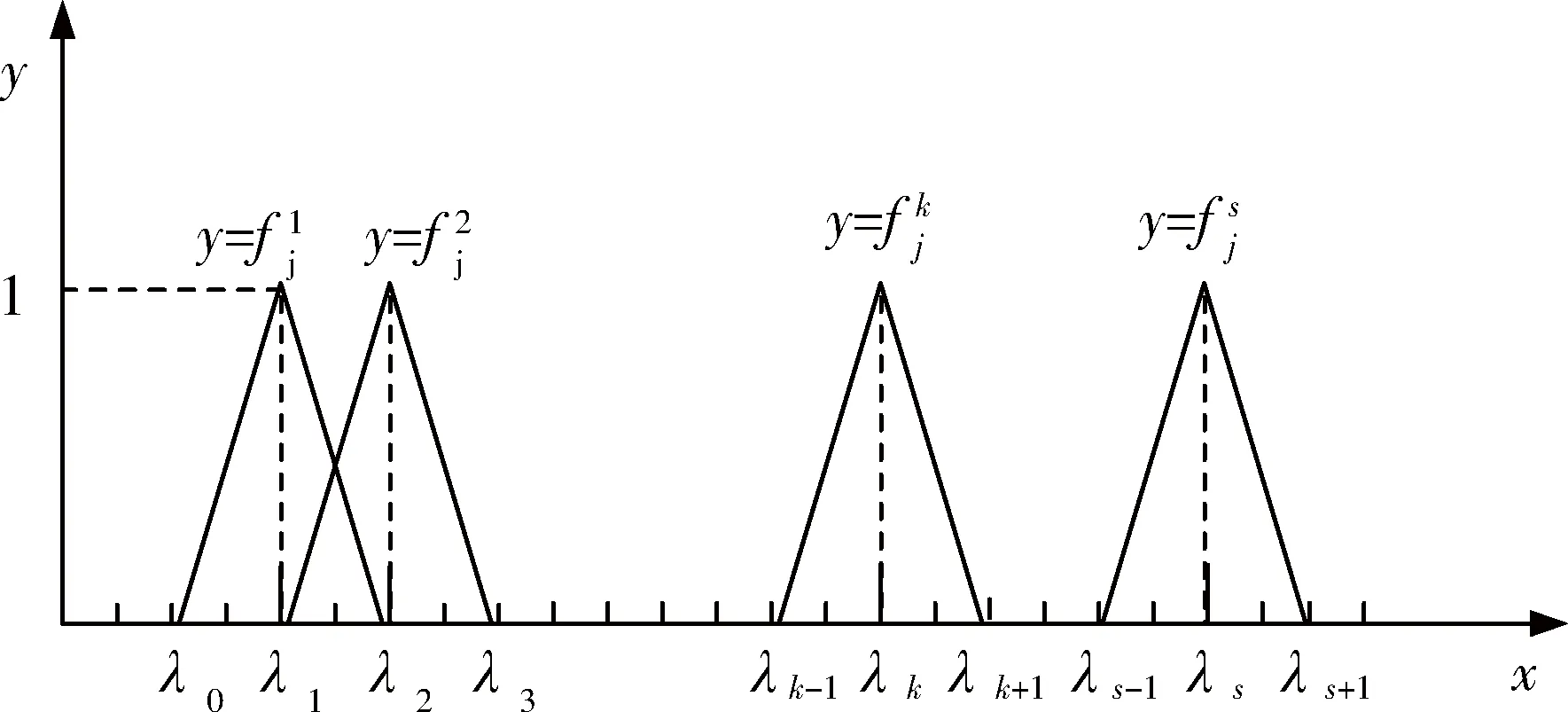
图1 中心点三角白化权函数

指标j属于灰类k的隶属度fjk(x)为

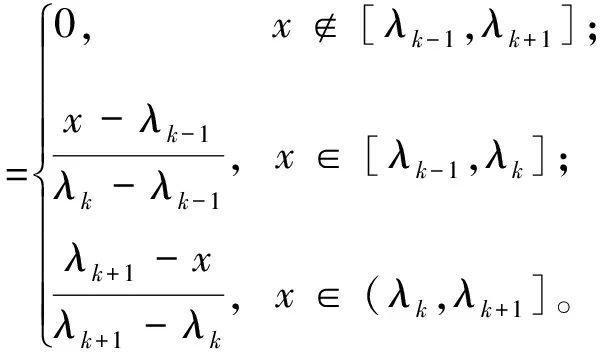
(4)

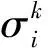
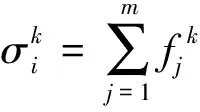
(5)

式中：fjk(xij)为指标j属于第k个灰类的白化权函数值，ηj为指标j在综合聚类中的比重。

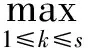
3 实例分析

以空军场站某型飞行保障装备维修合同商的服务质量评价为例，邀请相关专家、上级机关人员、部队相关主官及装备操作使用人员共10人组成评估小组，对该装备维修合同商的服务质量进行评价。

3.1 指标权重确定

首先采用FAHP法构造各层评价指标的模糊互补判断矩阵，然后根据式(1)-(3)得出一级指标的权重为

w=(0.237 3,0.136 7,0.220 6,

0.104 9,0.121 7,0.178 8)。

二级指标的权重分别为

w1=(0.149 3,0.294 7,0.283 6,0.272 4)；

w2=(0.246 3,0.253 0,0.268 8,0.231 9)；

w3=(0.348 1,0.330 9,0.321 0)；

w4=(0.372 7,0.627 3)；

w5=(0.458 2,0.541 8)；

w6=(0.239 5,0.251 6,0.247 9,0.261 0)。

3.2 确定评价灰类和三角白化权函数

采用4个评价灰类k=1,2,3,4分别表示“差”、“一般”、“良”和“优”4个评估等级。结合专家意见，确定各指标所属灰类的中心点分别为λ1=0.3，λ2=0.4，λ3=0.6，λ4=0.8，将灰类向两边延拓，得到中心点λ0=0.2和λ5=0.9。根据2.2节步骤2)可得中心点三角白化权函数fjk(x)分别为

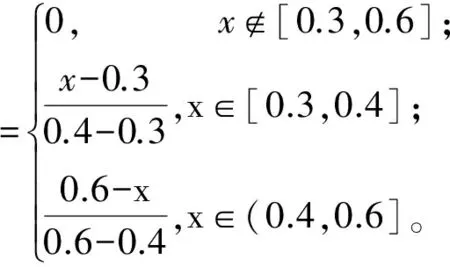
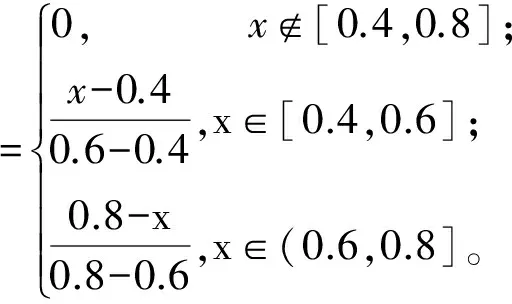
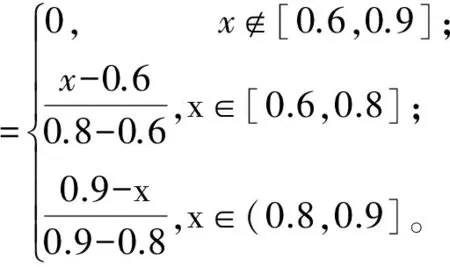
3.3 指标评价值确定和各指标白化权函数值计算

根据该装备维修合同商在合同期内的表现和装备的良好状况，邀请评审专家组对各指标进行打分，且分值在0.1～0.9之内，指标值越高表明合同商的服务质量越好。表3为10位专家对装备维修合同商服务质量二级评价指标的打分结果，结合实际情况，取打分平均值作为指标的最终评价值。

根据式(4)可得各二级指标的白化权函数值fjk(xij)，具体如表4所示。

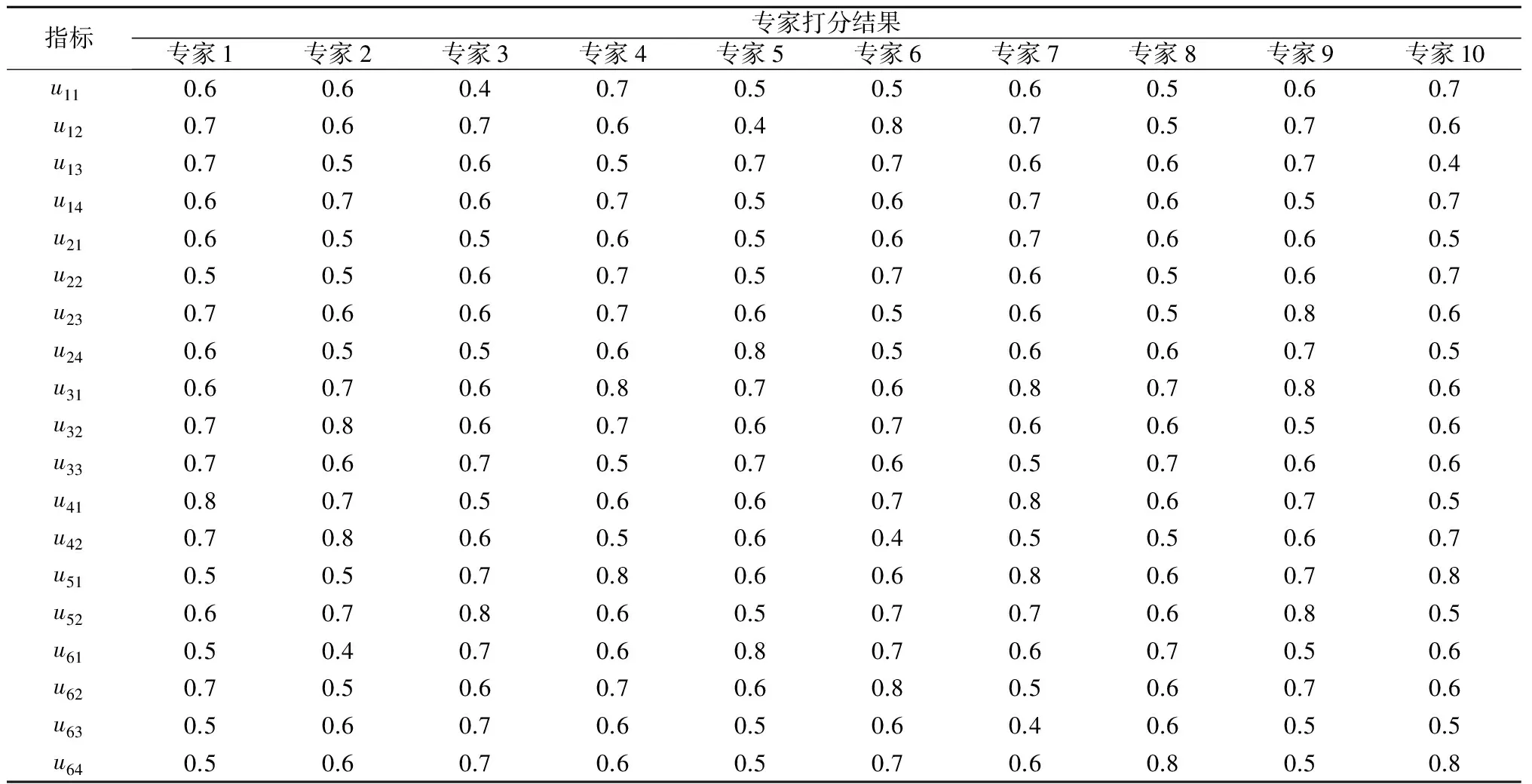
表3 10位专家对二级指标的打分结果

3.4 结果分析

根据式(5)可得装备维修合同商服务质量一级评价指标的聚类系数和服务质量综合聚类系数，如表5所示。

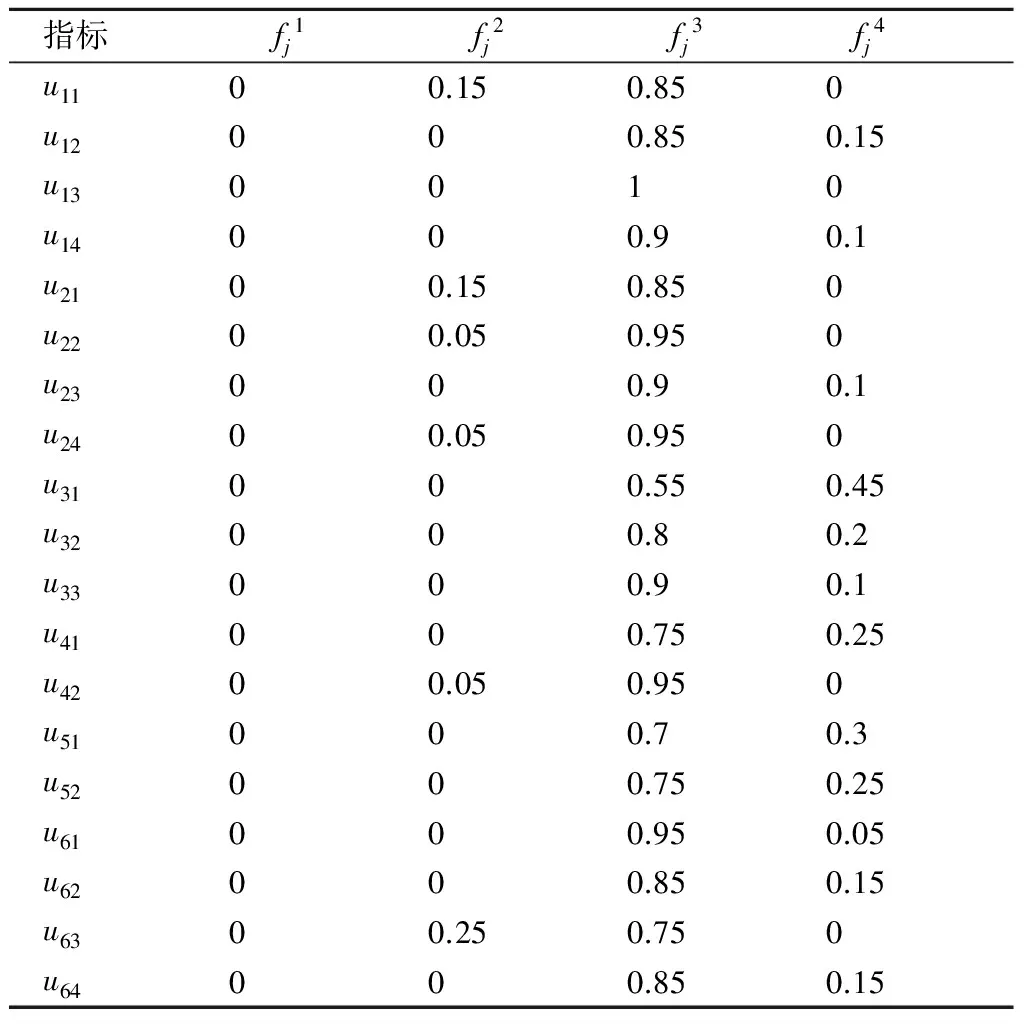
表4 各二级指标白化权函数值

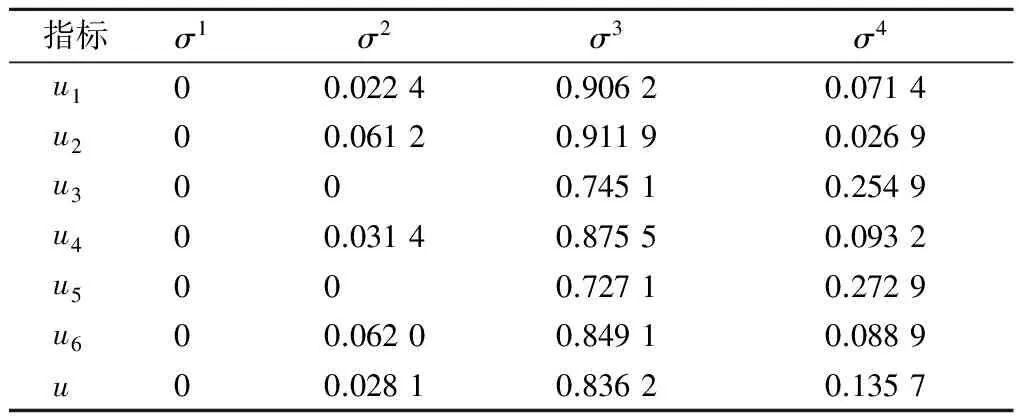
表5 一级指标聚类系数和综合聚类系数

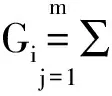
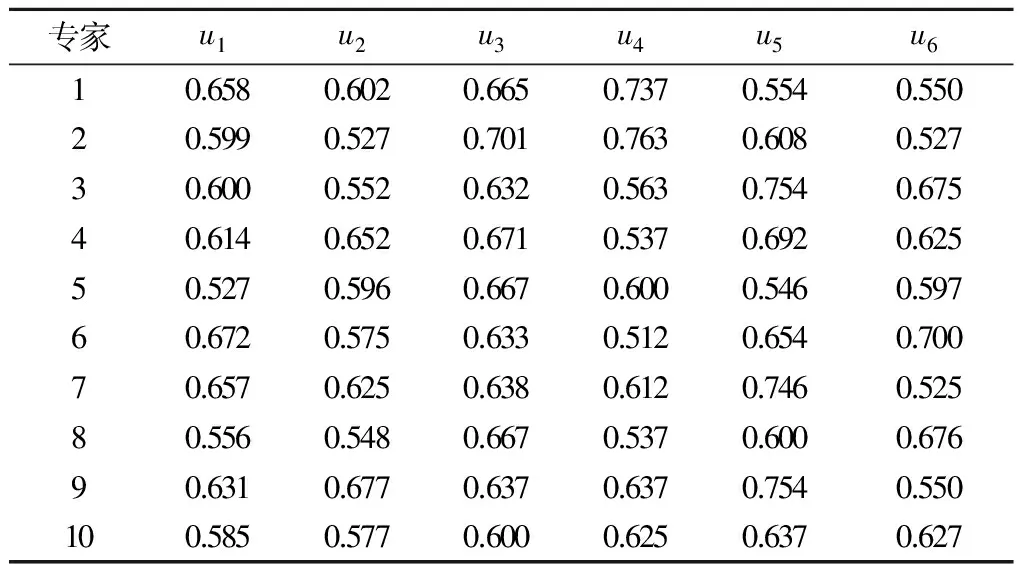
表6 一级指标打分结果

根据表6可得装备维修合同商的服务质量评价矩阵H，则该维修合同商的服务质量评价值为

R=A×H×wT=

[0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1]×

可见，该装备维修合同商的服务质量评级为“良”，与笔者得出的结论一致。所以，笔者提出的评估模型是可行的。

4 结论

笔者建立的基于FAHP和中心点三角白化权函数的评估模型能够对装备维修合同商的服务质量进行较为客观、合理和全面的评估，对合同交付阶段科学评价装备维修合同商的服务质量具有一定参考价值。但由于指标量化过程中过分依赖专家经验，一定程度上影响了评价结果的客观性，下一步将重点加强指标数据的收集，以及指标体系的优化。

[1] 吕岳卿， 李鹏举， 蔡丽影， 等. 战时合同商保障风险评估研究[J]. 军械工程学院学报， 2011, 23(6)： 1-4.

[2] 李环林. 军民融合装备保障[M]. 北京： 解放军出版社， 2009： 163-178.

[3] 杨华， 吴巧云. 装备维修合同商保障风险识别与评估研究[J]. 装备学院学报， 2013, 24(3)： 49-52.

[4] 袁良运， 赵以贤， 宋贤龙. 基于三角模糊熵的装备维修合同商评价与选择[J]. 火力与指挥控制， 2013, 38(6)： 85-88.

[5] 郑桂凯， 苏凡囤， 王海涛， 等. 基于模糊综合评价的工程装备维修保障合同商选择[J]. 工兵装备研究， 2014, 33(2)： 55-59.

[6] 党伟， 车飞. 基于模糊数的装备保障合同商选择决策方法[J]. 火力与指挥控制， 2013, 38(12)： 39-42.

[7] 曹会智， 杨超， 单长华， 等. 基于叶贝斯网络的后勤装备维修合同商保障风险识别与评估[J]. 四川兵工学报， 2013, 34(1)： 93-100.

[8] 侯小燕， 王国忠. 基于模糊综合评判的装备合同商服务质量评估[J]. 兵工自动化， 2009, 28(12)： 42-44.

[9] 胡玉清， 张桦， 张帅. 装备维修合同商绩效评估指标体系研究[J]. 价值工程， 2012, 31(2)： 114-115.

[10] 陈国生， 谭良才， 徐长江. 基于灰色聚类的防空旅战斗保障体系效能评估[J]. 兵工自动化， 2015, 34(4)： 60-63.

[11] 阎连新， 单长华， 李沛， 等. 合同商服务质量评估方法[J]. 四川兵工学报， 2013, 34(7)： 67-70.

[12] 万君， 刘馨. 服务质量研究的现状及其发展趋势[J]. 现代管理科学， 2014(5)： 65-66.

[13] 周媛媛， 周学军， 田培根， 等. 模糊层次分析法在海缆安全评估中的应用[J]. 海军工程大学学报， 2014, 26(4)： 59-62.

[14] 闫宝会， 刘晓东， 吴诗辉， 等. AHP和三角白化权函数的武器装备研制技术风险评估[J]. 火力与指挥控制， 2016, 41(1)： 178-181.

[15] 王昌金， 张永辉， 黄彬. 要地防空指挥控制系统作战效能灰色聚类评估[J]. 现代防御技术， 2013, 41(4)： 61-67.

(责任编辑:王生凤)

Service Quality Evaluation of Equipment Maintenance Contractor Based on Triangle Whiten Weight Function

WANG Shuang-chuan1, LÜ Rui-qiang1, HU En-yong2, YANG Yang1

(1.Department of Aviation Four Stations, Air Force Logistics College, Xuzhou 221000, China； 2. Training Department, Air Force Logistics College, Xuzhou 221000, China)

Aiming at evaluation of the service quality of equipment maintenance contractor in the stage of delivering contract, the index system of service quality evaluation for equipment maintenance contractor is established. Index weights at all levels are calculated by the method of fuzzy analytical hierarchy process(FAHP), and a service quality evaluation model of equipment maintenance contractor is proposed based on central point triangle whiten weight function. Finally, the practicability and validity of the model are verified by an example.

fuzzy analytical hierarchy process; triangle whiten weight function; equipment maintenance contractor; service quality evaluation

1672-1497(2016)05-0020-05

2016-05-16

王双川(1992-)，男，硕士研究生。

E257

A

10.3969/j.issn.1672-1497.2016.05.004