基于聚类综合评价值的灰色决策模型

赵维涛，胡东超，尹福平

(沈阳航空航天大学 航空宇航学院, 沈阳 110136)

1 引言

灰色决策通过多个不同的决策指标对决策对象进行分类和优选，可以有效处理多目标多准则分类与优选问题。灰色决策方法提出以来，被大量应用于各类评估实践。2017年，Cao等结合层次分析和灰色聚类法建立了老龄导管架平台安全评估模型。2017年，Mao等将分数阶灰色累加算子应用于城市交通流的预测与分析。2019年，李建华等使用灰色理论构建了装备维修经费投入预测模型。2019年，E等将模糊灰色关联理论应用于微型涡轮发动机燃烧特性影响分析。2020年，范纪松等将多层次灰色关联分析理论和层次分析法进行结合，应用于合成旅工程保障能力评估。2020年，胡昌栋等将灰色层次分析方法应用于机动通信系统效能评估。2020年，Yu等将改进灰色聚类法应用于复合材料无损检测的评估之中。2021年，Su等将灰色关联聚类应用物业服务满意度分析。2021年，梁振刚等基于蒙特卡洛抽样方法和灰色系统理论建立子母弹对机场目标毁伤效能计算模型。

在灰色决策方法应用的同时，众多学者对灰色决策理论进行了研究和改进。2016年，Liu等提出了一种基于灰色累加生成算子的灰数预测模型。2019年，Gao等提出了基于分数阶弱化缓冲算子的灰色预测模型。2021年，周弘扬等将D数理论与灰色理论用于改进层次分析法。2021年，张军涛等以模糊数学和关联函数理论为基础，提出了基于灰色关联-模糊综合评判方法。范纪松等传统模型中的调整系数向量进行重新设计，优先结果相对传统方法有所改进。

目前，灰色决策在实际工程中获得了广泛应用。然而，传统灰色决策中综合决策测度仅能对同灰类决策对象进行优选，优选结果是建立在分类准确的基础上。但在实际运用中，往往会遇到决策系数无显著性差异等情况，此时无法进行准确分类。如果基于存在偏差的分类进行优选，这种偏差会被继承且放大。另外，综合决策测度构造不合理，对除第1灰类外的其他灰类，排序结果可能与实际不符。为解决以上问题，以聚类综合评价值表征评估结果，提出基于聚类综合评价值的灰色决策模型。

2 传统方法

传统方法是根据白化权函数对决策对象的待评估决策指标样本值按几个灰类进行归纳，以判断该决策对象最可能隶属于哪个灰类，再根据综合决策测度对同一灰类评级的决策对象进行排序优选。

2.1 基本方法

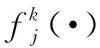
(1)

当有多个对象属于灰类时，对象综合决策测度为

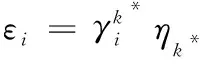
(2)

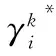
若>，则在灰类中，对象优于。

2.2 缺陷分析

传统方法包含分类与优选2个步骤，以聚类系数进行分类，以综合决策测度对同灰类对象进行排序，然后将各个灰类的排序按灰类高低合并成总的排序结果，进而优选。在实际运用中，传统方法有时会给出不合理的优选结果。

例如设有高、中、低3个灰类，对象1和对象2聚类系数向量分别为{040,017043}、{000,057,043}，通过隶属度的比较即可判断对象2优于对象1。具体说明如下：对象1对“高”灰类隶属度高于对象2，对“中”灰类隶属度低于对象2，对“低”灰类隶属度与对象2相同，因而对象1应优于对象2。按传统方法对象1属于“低”灰类，对象2属于“中”灰类，因综合决策测度无法对不同灰类决策对象进行排序比较，只能根据灰类高低判断优劣，排序结果为对象2优于对象1，排序结果与实际相反。

现有调整系数向量设计存在缺陷，本灰类权值(调整系数)比优于本灰类的灰类权值更高，造成本灰类决策系数越大的决策对象，排序结果越靠前。对第1灰类是合理的，但对第(=2,3,…,)灰类，尤其是第灰类，决策排序结果可能与实际不符。另外，在优选时，样本值高且分布稳定的决策对象应优于样本值低且分布不稳定的决策对象，但传统灰色决策并未考虑样本值分布是否稳定，即未考虑系统数据(规范化无量纲样本值)的离散程度，具有一定的片面性。

3 基于聚类综合评价值的灰色决策

将分类与优选作为整体考虑，在传统模型仅考虑各灰类决策系数的基础上，进一步考虑各指标样本值、各灰类临界值以及系统数据离散程度，将样本蕴含的信息充分利用，分类与优选在理论上相比传统模型更具客观性。本文方法的具体步骤如下：

1) 数据处理

将指标样本值进行无量纲化处理，将量纲数据转化为0～1之间的无量纲数据。

2) 指标权重及白化权函数

按照传统方法确定各指标权重及白化权函数。

3) 归一化白化权函数

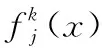
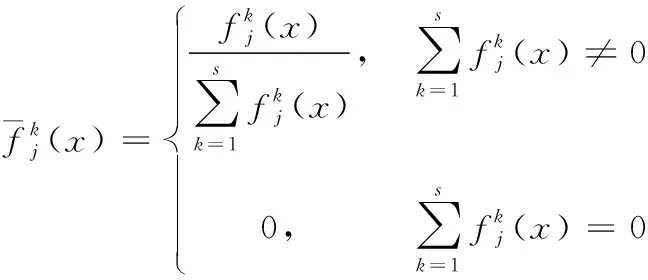
(3)

4) 归一化聚类系数

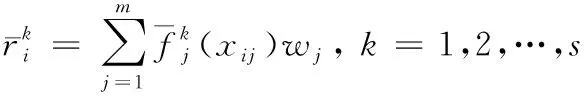
(4)

5) 聚类综合评价值

在加权平均原则基础上，进一步考虑样本标准差，给出聚类综合评价值概念，提出一种新的灰类量化取值方法。

聚类对象的聚类综合评价值为

(5)

式中：为第灰类量化值；为聚类对象的无量纲样本标准差；()为的函数。

在灰类量化时，取落在灰类的各个样本值的平均值为该灰类量化值。若某个灰类没有样本值，则取该灰类临界值为该灰类量化值。可通过白化权函数确定，相关定义及计算可参见文献[1]。

函数()为无量纲样本标准差的函数，采用分段函数表示，为

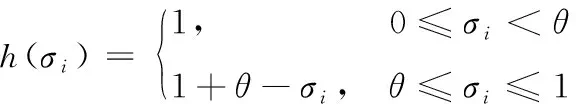
(6)

式中：为标准差临界值，为相邻2个灰类样本值对应标准差的加权平均值，权值为相应灰类隶属度。

从式(5)可以看出：聚类综合评价值综合考虑各灰类的聚类系数、各灰类临界值、各样本值以及系统数据的离散程度(标准差)，能够将少量样本的信息充分利用，聚类结果在理论上相比传统模型更具客观性。

6) 分类与优选

以相邻灰类白化权函数交点为区间边界，结合上下限，给出s个灰类区间，聚类综合评价值落在哪个区间，聚类对象就属于哪个灰类。

根据聚类综合评价值数值大小，对决策对象进行排序比较，聚类综合评价值越大，排序结果越靠前。根据决策要求需要的目标个数，选择排序靠前的对象为优选结果。

4 算例

4.1 算例1

该算例为防空武器毁伤能力评价与选择，分为更优、优、良、中、差、更差6个灰类。采用基于中心点的三角白化权函数，各灰类取值范围分别为[0.825，1.0]、[0.675，0.825]、[0.525，0.675]、[0.375，0.525]、[0.225，0.375]、[0.000，0.225]，灰类临界值分别为0.9、0.75、0.6、0.45、0.3、0.15，指标权重依次为0.245 1、0.127 8、0.251 7、0.253 9、0.121 5。指标无量纲化样本值(评分值)见表1，本文方法的计算结果见表2所示。

表1 指标无量纲化样本值Table 1 Non-dimension index value

表2 计算结果(算例1)Table 2 Results of example 1

传统方法首先利用聚类系数对指标进行分类，然后利用综合决策测度对同灰类指标进行排序。传统方法排序结果为>>>>，分类结果为属“更优”，属“优”，、和属“良”；本文方法排序结果为>>>>，分类结果见表2。本文方法计算结果与传统方法计算结果有所不同，具体说明如下：

1) 样本与样本

对于分类结果，从表2可知，样本对“更优”和“良”灰类的聚类系数分别为0373和0393，差异十分微小。当采用聚类系数的最大值(传统方法)作为分类结果，从数学理论上讲，存在一定评估风险。当最大隶属度(“良”灰类)和第二大隶属度(“更优”灰类)相差较小时，分类结果应与二者对应灰类等级的平均状态“优”大体相当。然而，传统方法分类结果为“良”，分类结果偏于保守。

对于排序结果，样本和样本归一化聚类系数向量分别为{0373,0034,0393,0000,0000,0000}、{0033,0574,0393,0000,0000,0000}，二者对“良”、“中”、“差”、“更差”灰类隶属度相同，因此可以把这4项从分析中去掉，通过对其他灰类(“更优”和“优”)隶属度即可判断样本与样本的优劣。样本对“更优”灰类隶属度高于样本，对“优”灰类隶属度低于样本，说明样本相比样本倾向于更高灰类。另外，对表1中指标评分值进行分析，样本的指标3、4和5评分值与样本相同，指标1、2评分值比样本高，即样本应优于样本。综上所述，无论比较隶属度，还是比较指标评分值，样本都应优于样本，而传统方法排序结果样本优于样本，排序结果错误。

2) 样本、样本与样本

传统方法排序结果为>>，排序结果错误，具体解释如下：灰色决策模型是根据多个不同指标对样本进行排序比较，当单独按任意指标的排序结果都一致时，灰色决策模型的排序结果也应与按任意指标的排序结果一致。从表1中的评分值可知，对于5个指标的评分值，样本均大于样本、样本均大于样本，即对所有指标而言，样本均优于样本、样本均优于样本。因此，实际排序结果应为>>。

3) 讨论

传统方法结果不合理的主要原因是：传统模型的综合决策测度仅能对同灰类决策对象进行排序，对于不同灰类决策对象间的排序则直接继承分类结果，样本分类不合理将被排序结果继承并放大。

本文模型的聚类综合评价值可对属于不同灰类的所有决策对象进行排序，排序结果不受分类结果影响；能够减少因聚类系数无显著差异引起的分类错误的风险，能够避免因不合理分类引起排序结果偏离实际的现象，分类与优选结果更客观。

4.2 算例2

该算例来源文献[15]，为武器装备供应商的评价与选择，分为优、良、中、差4个灰类。各灰类取值范围分别为[085，10]、[075，085]、[065，075]、[00，065]，各个灰类临界值分别为09、08、07、06。各指标无量纲化样本值、权重及白化权函数见文献[15]。本文方法的计算结果见表3所示。

表3 计算结果(算例2)Table 3 Results of example 2

传统方法排序结果为>>。本文方法排序结果为>>。本文方法排序结果与传统方法排序结果不同，具体说明如下：

1) 样本与样本

传统方法排序结果为样本优于样本，排序结果不合理。具体解释为：对比表3中样本与的数据可知，按最大隶属度原则，样本与均属于“良”灰类，但样本对“优”灰类隶属度优于样本，对其他灰类隶属度劣于样本，即样本倾向于更高灰类、样本倾向于更低灰类。另一方面，对于样本的最大隶属度0369与“优”灰类隶属度0327接近，即样本相对偏向“优”灰类；而样本，其最大隶属度0385与“中”灰类隶属度0354接近，即样本偏向于“中”灰类。综上所述，样本是优于样本的。

2) 讨论

造成传统模型排序结果不合理的主要原因是：传统模型利用综合决策测度进行排序，本灰类权值(调整系数)比优于本灰类的灰类权值更高，造成本灰类决策系数越大的决策对象，综合决策测度必然也越大。对第1灰类(最优灰类)是合理的，但对其他灰类，排序结果可能出现不合理现象。

本文模型用聚类综合评价值取代传统方法中的综合决策测度，能够避免因综合决策测度中的调整系数向量构造不合理引起的排序偏差。本文模型同时考虑了指标样本值、各灰类临界值及样本离散程度，将样本蕴含的少量信息充分运用。本文模型排序结果与文献[15]通过重新设计调整系数向量得到的排序结果一致。

5 结论

1) 以聚类综合评价值取代传统模型中的综合决策测度，提出了一种基于聚类综合评价值的灰色决策模型。该模型将分类与优选作为整体考虑，突破了传统模型需要决策对象属于同灰类的限制，可同时对所有灰类决策对象进行排序优选，排序结果不受分类结果影响。聚类综合评价值能够综合考虑各灰类归一化聚类系数、各灰类临界值以及系统数据离散程度，能够将少量样本信息充分利用，分类结果与排序优选结果在理论上比传统模型更具客观性。

2) 本文模型既能避免因综合决策测度中调整系数向量构造不合理引起的排序偏差，也能消除综合决策测度仅能对同灰类决策对象进行排序的限制，同时还能减少聚类系数无显著差异而引起的不合理排序及错误决策风险。算例表明，本文模型合理有效，分类与优选比传统模型更加客观。