改进的灰色聚类模型在鞍山地区地下水质综合评价中应用

马 猛

(辽宁省本溪水文局，辽宁 本溪 117000)

鞍山位于辽宁的中部平原区域，区域地下水资源较为充沛[1]。近些年来，受人类活动影响，区域地下水资源质量受到不同程度的影响，部分区域地下水质状况有所恶化[2]。亟需要对区域地下水质进行安全评估，从而制定相对应的地下水资源量保护措施[3]。而地下水质影响因素较多，很难进行有效综合评价，当前，对于地下水质评价国内取得一定研究成果[4-7]，并研究出一套地下水质综合评价的指标体系，该指标体系已在国内许多地区地下水综合评估中得到应用[8-10]。在指标体系的基础上，需要选用一种较为合理的评估方法对区域地下水质进行综合评估，这其中灰色聚类模型由于可考虑不同指标之间的关联度，在许多地区地下水综合评估中应用效果较好[11-12]，但一些研究成果表明灰色聚类模型由于其指标权函数存在单一纤细变化的局限，往往很难得到收敛解。为提高区域地下水质综合评估的精准度，文章采用非线性变化权函数对灰色聚类模型进行改进，对鞍山地区地下水质进行综合评估，研究成果对于区域地下水质综合评估具有重要参考意义。

1 模型改进原理

灰色聚类模型结合地下水质综合评估指标体系划分成不同评价等级，各评估等级的取值域分别为为[xj1，xj2]，[xj2，xj3],...[xjn，xjn+1]，评估指标个数采用j进行表述。模型将第一评价等级的权函数设定为xj1，则第n个评价指标的权函数为xjn：

(1)

式中：fn(xj)为各指标权函数的灰类值；xj为地下水质评价指标，一般为测定的某类水质监测指标；λn及λn-1为第n和第n-1灰类指标的权函数值。改进模型对各灰类指标的权函数进行标准化处理后，对综合聚类系数进行计算：

(2)

式中：σjk为地下水质综合聚类系数；gjk(xj)为灰类指标权函数的标准化处理值；wj为指标权重。模型对各灰类指标结合权函数进行地下水质评估度的综合计算：

(3)

式中：djn为综合评估度；xjn+1、xjn、sjs、xj1为地下水质指标不同水质类别对应的取值范围区间。在综合评估度的计算上，模型结合指标区间对其相对综合评估度dk进行计算：

(4)

2 模型应用

2.1 监测数据情况

文章结合鞍山地区6个地下水监测点的水质监测数据进行地下水质综合评估分析，各水质监测点的水质采样分析数据。鞍山地区地下水质监测点水样分析数据，见表1。

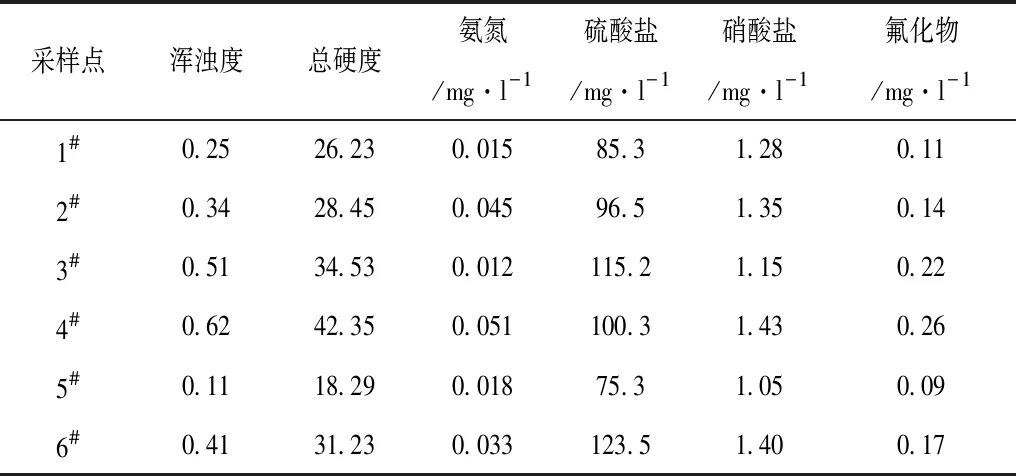
表1 鞍山地区地下水质监测点水样分析数据

2.2 评估等级的划分

结合水质分类标准对地下水质综合评估指标进行不同等级的划分，地下水综合评估等级划分结果，见表2。

表2 地下水综合评估等级划分结果

2.3 各灰类指标权函数计算值

对不同灰类指标进行权函数进行计算，不同灰类指标权函数计算值，见表3。

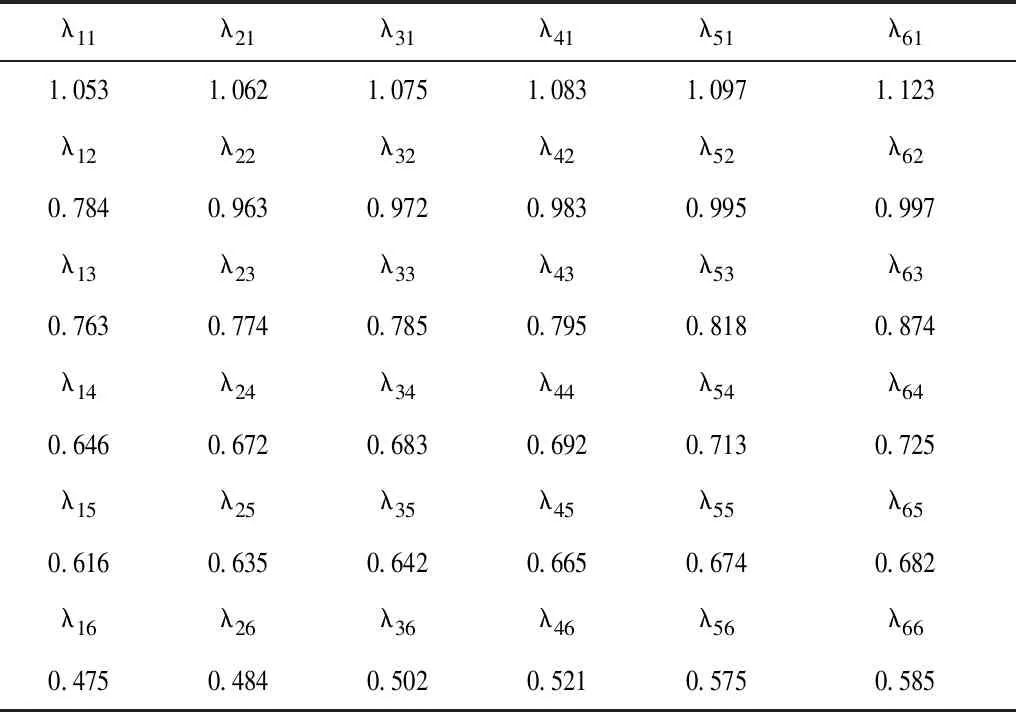
表3 不同灰类指标权函数计算值

2.4 灰类指标权函数标准化处理

在各灰类指标权函数计算的基础上，对各灰类指标的权函数进行标准化计算。各灰类指标权函数标准化处理值，见表4。

表4 各灰类指标权函数标准化处理值

从分析结果可看出，不同地下水质采样点各灰类水质指标权函数经过标准化处理后呈现显著非线性变化，各灰类指标值与权函数具有较高的相关度，指标浓度越大其权函数相对较大。

2.5 灰类指标权重计算

采样专家赋分方式对不同评价指标的权重值进行计算。各灰类评价指标权重值，见表5。

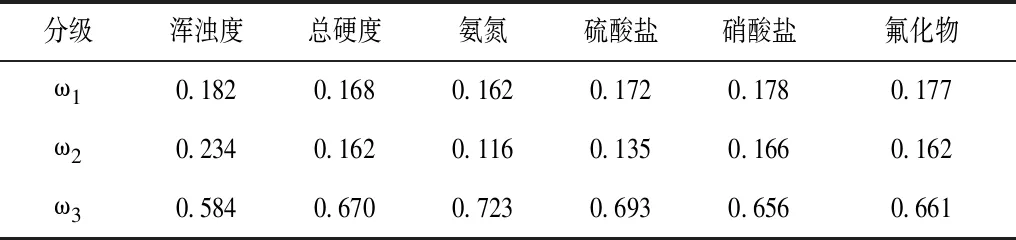
表5 各灰类评价指标权重值

2.6 综合聚类系数计算

在各灰类指标权重以及权函数标准化处理的基础上，结合改进灰色聚类模型的平均指标的综合聚类系数计算方法，对各地下水采集点不同等级下灰类指标的综合聚类系数进行计算，不同灰类指标的综合聚类系数的计算结果，见表6。

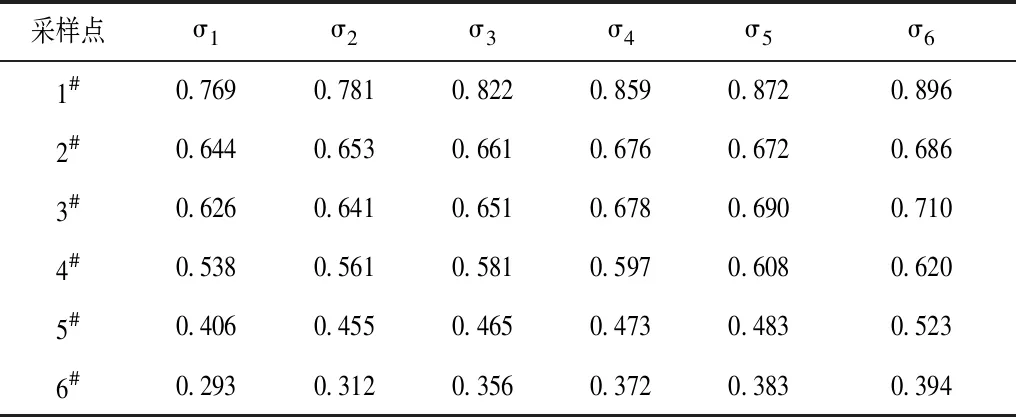
表6 不同灰类指标的综合聚类系数的计算结果

从分析结果可看出，不同地下水采集各灰类指标综合聚类系数总体呈现递增变化，主要受各灰类评价指标聚类系数累积求和影响所致，使得在进行综合聚类系数时不同灰类指标呈现较为明显的递增变化，不同地下水监测点各指标综合聚类系数均<1，模型计算结果具有合理性。

2.7 地下水质综合评估

分别采用改进前后的的灰色聚类模型，对鞍山地区各地下水监测点水质进行综合评估。不同等级地下水质综合评估结果，见表7。

对鞍山地区6个地下水质监测点不同等级下的地下水质进行综合评估，通过评估结果可看出，采用改进模型下综合评估结果总体要低于传统模型，这是因为改进模型对不同灰类指标的权函数进行非线性处理，解决传统模型灰类指标权函数采用线性处理方式的局限，提高模型的收敛精度。区域地下水质影响因素较多，模型评估指标也较多，而若采用线性权函数的方式不能完全表征不同灰类水质评价指标的关联程度，因此其评估结果总体要低于改进模型。通过对区域地下水质进行实地调查，改进模型评估结果更符合区域实际情况，评估结果的合理性好于传统模型[13-14]。

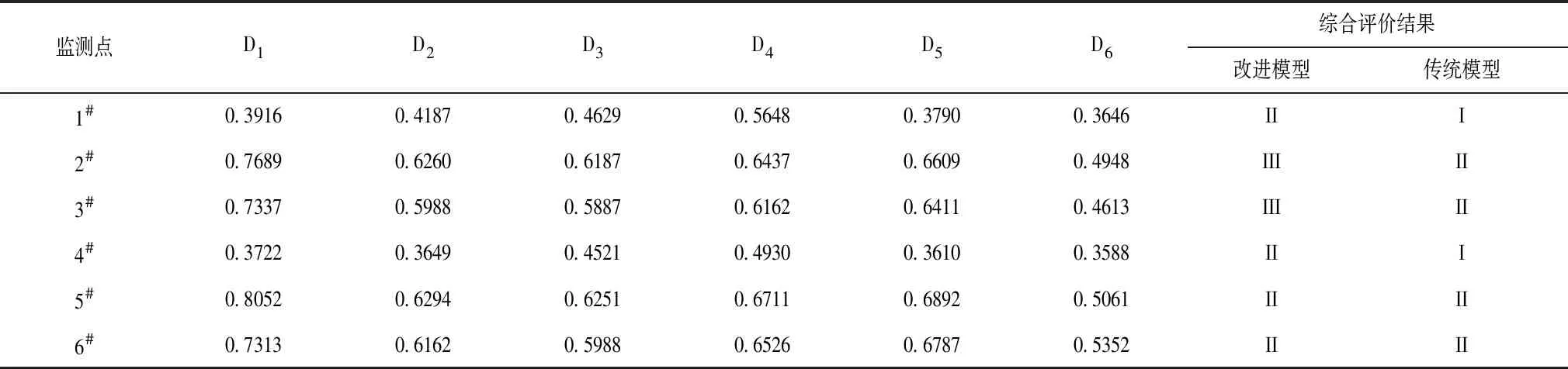
表7 不同等级地下水质综合评估结果

3 结 论

1)不同地下水质采样点各灰类水质指标权函数经过标准化处理后呈现显著非线性变化，各灰类指标值与权函数具有较高的相关度，指标浓度越大其权函数相对较大。

2)不同地下水采集各灰类指标综合聚类系数总体呈现递增变化，主要受各灰类评价指标聚类系数累积求和影响所致。

3)改进灰色聚类模型对不同灰类指标的权函数进行非线性处理，解决传统模型灰类指标权函数采用线性处理方式的局限，提高模型的收敛精度，地下水质综合评估结果的合理程度高于传统灰色聚类模型。