基于端点三角白化权函数的物流服务质量绩效灰色聚类评估模型

林小芳，夏慧玲，赵政华 （南通理工学院 商学院，江苏 南通 226002）

绩效管理作为一项复杂的系统工程，是企业管理的热门话题，而绩效评价又是绩效管理的核心所在。由于服务具有无形性、异质性、顾客参与性、不可储存性等特点，服务质量绩效的评价也具有较高的模糊性。物流业作为现代服务业重要组成部门，其质量绩效也越来越受到重视。服务质量绩效是实施服务质量管理的效率与效果，反映的是企业成绩或成果。本文结合国内外研究中给出的物流服务质量绩效评价指标体系，结合专家问卷调查，归类汇总指标，再利用端点三角白化权函数进行灰色聚类评价。

1 相关理论

1.1 质量绩效的维度。关于绩效的定义有三种：绩效是结果；绩效是行为；绩效包括行为和结果两个方面。质量绩效为企业的质量表现，主要表现为提升产品（服务）质量水平、降低过程质量损失、提升产品交付合格率等。服务质量绩效作为提供服务的结果，主要由服务内容、服务水平的高低以及客户对服务质量的预期需求与期望。由于质量定义的多样性，对质量绩效的构成维度也有不同的理解：Garvin[1]作为质量绩效研究的学者之一，最早提出了质量的8个维度；Curkovic[2]认为质量绩效的构成维度包含产品可靠性、耐用性、与性能标准一致性、设计的质量、公司声望、售前售后服务、对顾客需求的响应等。

1.2 质量绩效的评价。简单的指标组合并不能正确反映质量绩效的水平，因此必须采用合理的体系。学术界对此也展开了大量的研究。财政部等五部委联合发布《企业绩效评价细则（修订） （2002年）》将指标体系详细分为两种（定量、定性指标）并分别给出了各细分指标点、各指标的权重。其他学者也主要针对不同的行业，分别给出了具体指标。在评价方法上，多采用专家评分法进行指标的综合评价；同时，借助结构方程模型、贝叶斯网络、层次回归分析模型的混合使用，克服不确定性条件难以量化的缺点。

1.3 服务质量绩效。服务质量绩效与工业企业质量绩效的不同，源于无形服务与有形产品在特质上的差异。准确的服务质量绩效评价能够让企业识别服务质量存在的问题与不足，抓住关键指标，优化资源配置；有助于消除人为不公正、不客观的现象，为服务质量绩效的提升提供科学有效的依据。

现有文献对质量绩效的研究主要从组织和产品两个不同层面展开。关于产品质量绩效研究情况，如表1。而本研究在借鉴产品层面绩效的基础上，结合物流服务质量，给出物流服务质量绩效评价的测评指标。

表1 产品质量绩效指标

1.4 物流服务质量绩效指标体系。参考Dow，Samson，Haner，Kaynak等学者提出的质量绩效指标，再结合物流服务产品特点，访谈专家，给出了目标层、准则层（服务质量U1、过程质量U2、成本效益U3共3个一级指标），10个二级指标[3-4]。如图1。

2 三角白化权函数灰色聚类评价模型

近几年来，基于三角白化权函数的灰色评价方法被广泛用于各类评价实践中[5-9]。该方法最早由刘思峰提出，包括中心点三角白化权函数、端点三角白化权函数、梯形灰类白化权函数、等斜率白化权函数、共原点灰色白化权函数等[10]。但针对物流服务质量绩效的评价文献尚无。本研究考虑到评估指标灰类边界清晰，但属于各灰类点不明确，采用将端点三角白化权函数模型应用到物流服务质量绩效评估中去。分析物流服务质量的现状，以调研数据作为聚类对象，以服务质量绩效指标作为聚类指标，利用该聚类模型进行灰色聚类分析。

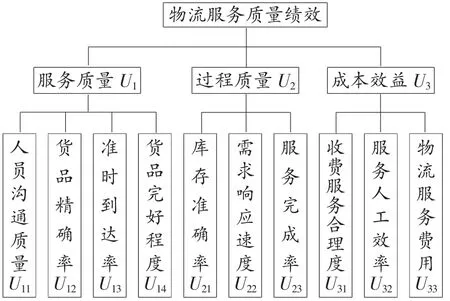
图1 物流服务质量绩效指标

采用灰色定权聚类评估模型进行物流服务质量绩效的评价，关键是确定j指标k子类白化权函数fjk（·）及确定各指标的聚类权wj。

2.1 评价指标体系权系数的确定。因层次分析法具有综合定性方法与定量方法的优点，故研究中采用层次分析法对指标体系的各指标进行权重标度。主要步骤如下：

（1）构造两两判断矩阵。按照确定的指标进行专家打分判断指标之间的相对重要度，构造两两判断矩阵A=aij（），aij表示i、j两元素相比不同的重要程度。根据定义可知aij与aji互为倒数关系，且aii=1。

（2）各层次指标相对于准则层权重的确定，可对判断矩阵采用求根法或求和法。首先对判断矩阵各列标度值进行归一化处理，得到新判断矩阵，即：；再对新矩阵B=bij（）按行求和，并将各和进行规范化处理即得到ωj即为第j个指标的权重。

（3）一致性检验。AHP法创始人Satty提出用平均随机一致性指标R.I.修正C.I.来进行一致性检验，即：C.R.=C.I./R.I.，其中为最大特征根，R.I.为平均随机一致性指标，取值如表2。

表2 平均一致性指标R.I.

当C.R.＜0.1时，认为判断矩阵具有较好的一致性，可接受。

（4）组合权重的确定。将上一层次指标层内权重值与下一层次层内指标权重相乘，便得到下一层次指标的综合权重。

2.2 构建灰类白化权函数。设有n个对象、m个评价指标，s个不同的灰类。对象i相对于指标j的样本观测值为xij，i=1，2，…，n；j=1，2，…，m。根据观测值对对象i进行评估诊断，过程如下：

（1） 确定评价灰类，共s个灰类。将各指标的取值范围相应划分为s个灰类，各灰类取值范围分别为区间 [a1，a2]，…，[ak-1，ak]，…，[as-1，as]，[as，as+1]，k=1，2，…，s。

（2）计算各区间的几何中点，设λk为第k个灰类的中心点，即最可能属于k分类的点。

（3） 将两端点向左右延拓，得到延拓后区间端点序列：a0，a1，a2，…，ak-1，ak，…，as-1，as，as+1。

（4）建立端点三角白化权函数：

（5）计算对象i关于灰类k的综合聚类系数即隶属度。

（6）根据隶属度最大原则判断对象i属于灰类k*。

3 算 例

采用上述端点三角白化权函数灰色聚类评价方法，选择4家物流服务企业A、B、C、D进行分析物流服务质量绩效的评价。

3.1 数据收集及指标权系数的确定。在国内外相关文献调研及现有成熟量表的基础上，结合物流企业专家访谈咨询意见，确定3个一级指标、10个二级评价指标构成的物流服务质量绩效评价体系。统计各位专家对各层次中各因素的两两比较判断矩阵，分别为 C1，C2，C3，C 如下：

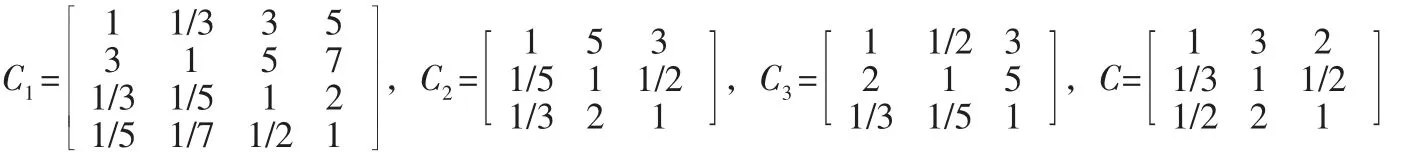
以上判断矩阵均通过一致性检验，检验结果如表3。

表3 两两比较判断矩阵一致性检验

由此计算得出指标层权重、准则层权重及组合权重，如表4。

表4 权重的确定

3.2 评价指标取值及延拓。为客观评价物流服务质量绩效，将评价灰类分为“差”、“中”、“良”、“优”4级。该文对10个二级指标灰类的划分不是真实阙值，只是评价对象间的相对比较。由评价专家依据掌握的信息采用百分制打分，采用相同的灰类划分临界值a1=55，a2=65，a3=75，a4=85，a5=95，并进行指标延拓a0=0，a6=100，并依公式（1） 计算中心点λk，如表5。

因为10个二级指标均为最大最优型，因此它们具有相同的白化权函数，本文仅给出第一个指标“人员沟通质量U11”的白化权函数：

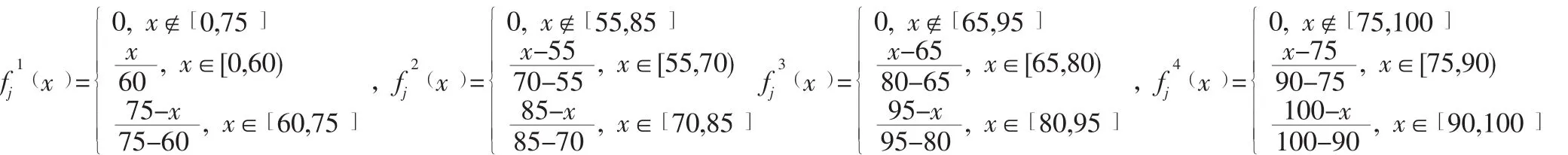
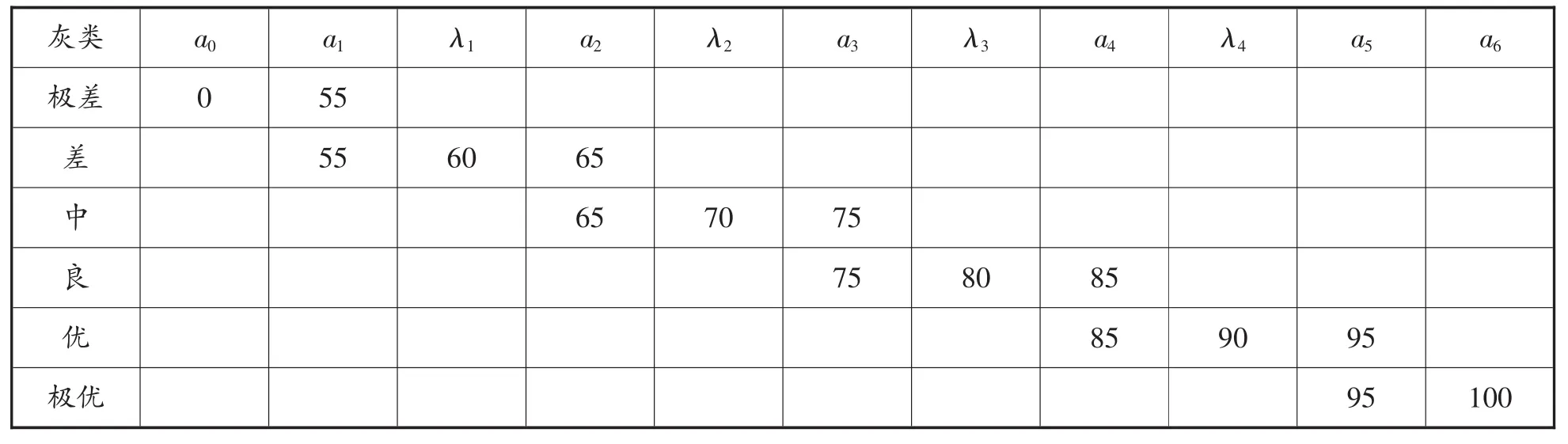
表5 延拓值、各灰类临界值ak及灰类中心点λk

3.3 各指标聚类系数和综合聚类系数的确定。针对指标体系中的j个指标，专家根据4个评价对象A-D的实际表现采用百分制给出各自评分（表6）。根据各二级指标实际值及权系数，利用端点三角白化权函数计算各评价对象各指标属于某灰类的隶属度，并根据综合聚类系数公式（3）得到4家物流企业的综合聚类系数，如表7。

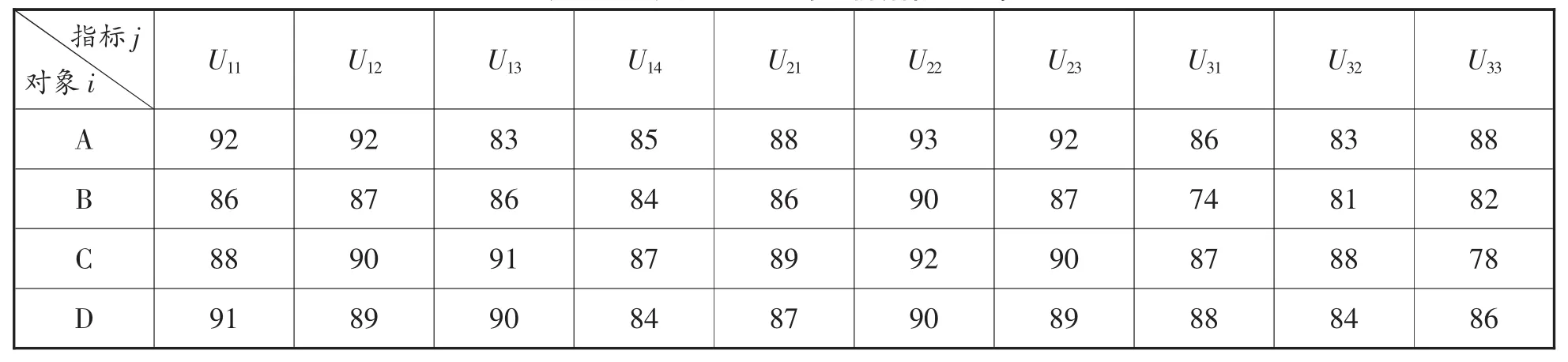
表6 4家物流企业的评价指标实际值

表7 各指标实际值、隶属度及所属灰类

4家物流企业属于“差”、“中”、“良”、“优”灰类的隶属度分别为：

4 结 论

（1）整体来看，物流企业A、C、D均属于“优”灰类，隶属度分别为0.735，0.89，0.838，说明该3家企业物流服务质量绩效处在相对较好的水平；物流企业B属于“良”灰类，隶属度为0.643，物流服务质量有进一步提升的空间。

（2）从各评价指标聚类系数即隶属度来看，A企业的U13，U32指标为“良”灰类，其它指标均为“优”灰类；B企业的U14，U32，U33为“良”灰类，U31为“中”灰类，其它指标为“优”灰类；C企业的U33为“良”灰类，其它指标为“优”灰类；D企业的U14、U32为“良”灰类，其它指标为“优”灰类。4家企业表现欠佳的指标集中在“货品完好程度”、“服务人工效率”等，B企业“收费服务合理程度”在很大程度商影响了该企业的整体质量绩效，有待较大幅度的提升。

（3）利用白化权函数的灰色聚类评估模型能够克服质量绩效模糊性的特点，能够全面地研判一家企业的质量绩效，且能够挖掘表现欠佳的指标，寻求服务质量的改善点。

[1]Garvin D A.Competing on the eight dimensions of quality[J].Harvard Business Review，1987，65：101-109.

[2]Curkovic S，Vickery S，Droge C.Quality-related action programs：Their impact on quality performance and firm performance[J].Decision Science，2000，31(4)：885-905.

[3]徐剑，刘俊强，方小昌.物流企业服务质量评价指标体系研究[J].物流科技，2006，29(1)：48-51.

[4]张阳，冯裕祺，康文婷.基于六西格玛的电商物流服务质量改进[J].物流工程与管理，2016，38(2)：25-27.

[5]石汝杰.基于三角白化权函数的重庆市水资源承载力灰色聚类评价[J].中国农业资源与区划，2015，36(6)：22-29.

[6]王双川，吕瑞强，胡恩勇，等.基于三角白化权函数的装备维修合同商服务质量评估[J].装甲兵工程学院学报，2016，30(5)：20-24，30.

[7]杨守德，赵德海.高校人才发展环境评价与选择研究——基于端点三角白化权函数的灰色聚类评估模型[J].广西社会科学，2016(8)：202-207.

[8]王化中，强凤娇.三角白化权函数灰色聚类决策下中小企业信用评价模型构建[J].企业经济，2014(4)：89-92.

[9]刘婷，肖长来，王雅男，等.基于中心点三角白化权函数的灰色评估法在地下水水质评价中的应用[J].节水灌溉，2013(5)：26-28，33.

[10]刘思峰，谢乃明.灰色系统理论及其应用[M].北京：科学出版社，2013.