风险因素影响下无人船智能路径规划方法

王澳刚，智鹏飞，朱琬璐

(江苏科技大学， 江苏 镇江 212000)

1 引言

路径规划是无人船能实现海上自主导航的重要组成技术之一，无人船路径规划通过对海洋环境信息进行分析，规划出一条安全且快捷的路径。近年来，随着无人船路径规划技术的不断发展，路径规划的最佳路径选取已经不只是考虑最小航行代价，还与路径的安全性、航迹的平滑度等诸多因素有关。目前无人船路径规划的算法主要有Dijkstra算法、A算法、D算法、蚁群算法、RRT算法等。Dijkstra算法采用贪心策略，适用于全局环境已知的情况。A算法采用启发式路径搜索，适用于全局环境信息已知的情况。D算法适用于环境未知或者环境存在动态变化的情况。蚁群算法相比于其他启发式算法具有较强的鲁棒性,易于融合改进。RRT算法适用于非完整约束的情况。

目前无人船在海上进行路径规划时，普遍使用A算法来实现。但是传统A算法进行路径搜索时，仅以航行代价作为考虑因素，没有考虑路径的安全性和存在多个最短路径时无法保证搜索的路径为最优等因素。文献[8]为避免无人船距离障碍物过近，对障碍物的边界进行了扩张，结果显示规划的路径能够有效避免危险区域；文献[9]提出在栅格地图中扩大A算法的搜索方向，来调整搜索路径中的冗余点与拐点。文献[10]通过将可搜索邻域拓展为无限个来获得最短路径；文献[11]将搜索到的路径代入三阶贝塞尔公式以获得连续的平滑路径。

本文中，主要针对传统A算法路径不平滑，折点多，路径单一的问题，提出了风险因素影响下无人船智能路径规划方法。

2 改进A*算法的无人船路径规划

2.1 基于栅格法的无人船航行环境模型构建

栅格法在无人船路径规划的环境模型建立过程中具有数据结构简单、便于转化操作等优点。为了能够方便的获取电子海图中的航行信息，需要先将电子海图转化为灰度图，灰度图二值化后生成黑白地图，其中黑色部分表示障碍物区域，白色部分表示可航行区域。在黑白地图中建立栅格坐标轴，、分别表示栅格的横坐标和纵坐标，赋予栅格地图中黑色障碍物部分状态值为(,)=1，白色可航行部分状态值为(,)=0。当无人船进行路径规划的路径搜索时仅读取栅格的状态值就能辨别当前位置是否为可航行区域。图1所示为某电子海图的栅格化环境模型。

图1 环境模型示意图

为了满足无人船在海上的实时自主导航要求，栅格地图中的坐标需要与电子海图中的经纬度坐标进行对应。将电子海图所跨越的经度分成份，所跨越的纬度分成份度。电子海图跨越的经度为最大经度减去最小经度，跨越的纬度为最大纬度减去最小纬度。设为无人船当前位置的经度坐标，为当前位置的纬度坐标，则电子海图中各经纬度坐标在栅格地图中对应的、坐标为：

(1)

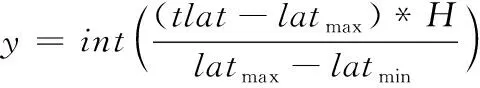
(2)

其中：为取整运算操作。

2.2 基于改进A* 算法的路径规划

基于传统 A算法的无人船路径规划仅以航行代价作为启发函数，不仅在存在多个最短路径时无法保证搜索的路径为最优，而且规划出的路径不能保证无人船在复杂海洋环境中航行的安全性和连续平滑。

针对无人艇路径规划的单一性问题，本文中，首先结合无人船的航行环境模型，引入障碍干扰值约束A算法的启发函数，越靠近障碍物的可行区域，其干扰值越大，以此建立无人船安全区域模型。然后利用变向干扰值约束对A算法进行航向优化。再利用贝塞尔曲线使航迹更加平滑连续，最后获得一条基于改进A算法的优化路径。

障碍干扰值约束下的A启发函数

基于上述构建的栅格化无人船航行环境模型，采用具有障碍干扰值约束的 A算法以实现路径规划。传统A算法的启发式函数表达式如下：

()=()+()

(3)

式中：()为当前栅格到起始栅格的航行代价；()为当前栅格到目标栅格的航行代价。

可知传统A算法的启发式代价函数仅为当前单元栅格到目标栅格的距离，没有考虑到在复杂海面上距离障碍越近的区域无人船遇到风险的概率越大的情况，所以应当引入障碍干扰值来优化A算法的启发式代价函数。

如图2所示，绿色区域是被赋予了障碍干扰值的区域，则当前栅格到目标栅格的航行代价为：

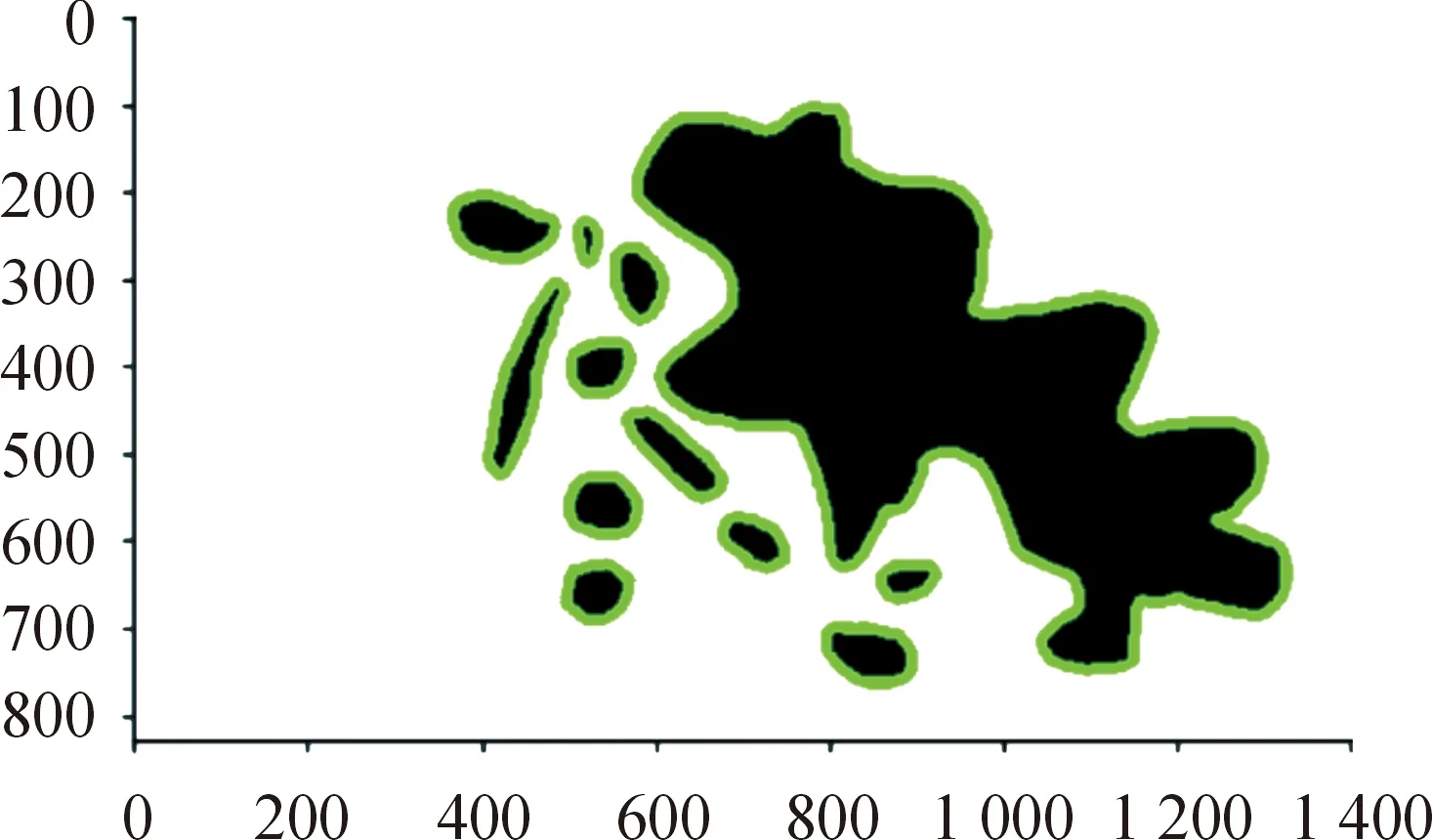
图2 障碍干扰值约束下的栅格示意图

()=()+()

(4)

式中：()为当前栅格到目标栅格的距离；()为当前栅格被赋予的障碍干扰值。

根据式(3)和式(4)，障碍干扰值约束下各栅格的启发函数可定义为

()=()+()+()

(5)

变向干扰值约束下的A启发函数

传统A算法下的无人船路径规划中路径会出现不必要的变向，从而出现连续“颤抖”现象，如图3中1处所示。但是，无人船的运动控制系统对路径的跟随能力不是无限的，规划的航行路径应该尽量减少变向的次数。1处红色路径的变向不符合无人船的运动规则，所以应该选择变向更少的2处的蓝色路径。针对这一问题，可以通过修改代价函数，来选择变向更少的路径。

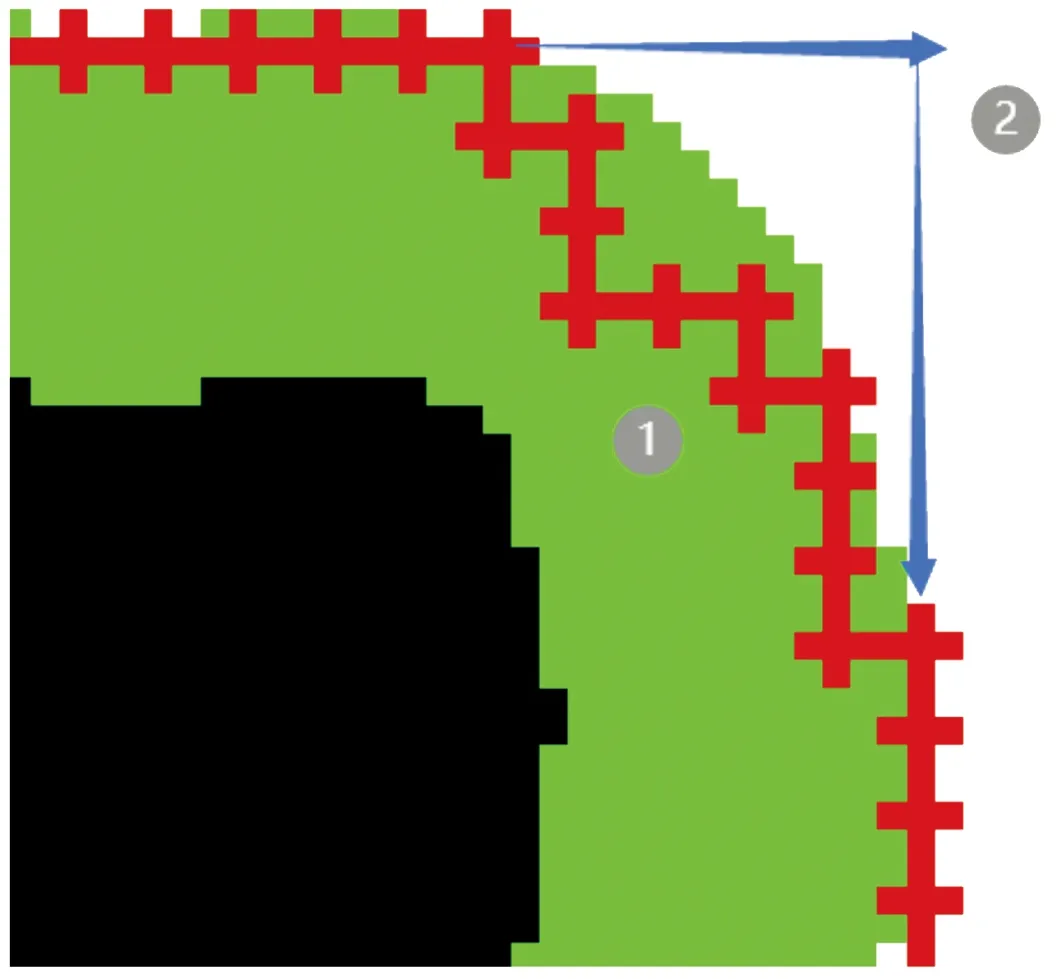
图3 A*搜索得到的两条距离相等路径示意图

无人船的航迹先尽量减少频繁的变向，尽可能的沿着一个方向航行。在栅格地图上，相同航行代价下的点越接近起点或是终点优先级越高。这里引入变向干扰值约束对路径进行选择优化，变向干扰值定义如下：

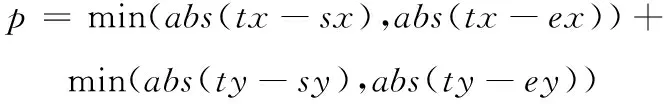
(6)

式中：为当前栅格横坐标；为起点栅格横坐标；为目的地栅格横坐标；为当前栅格纵坐标；为目的地栅格纵坐标；为目的地栅格纵坐标；(-)为水平距离(-)为垂直距离。

结合式(3)和式(6)，引入变向干扰值约束后，各栅格对应的启发式代价函数为：

()=()+*()+()

(7)

利用变向干扰值约束下的A算法进行路径搜索，得到如图4所示。

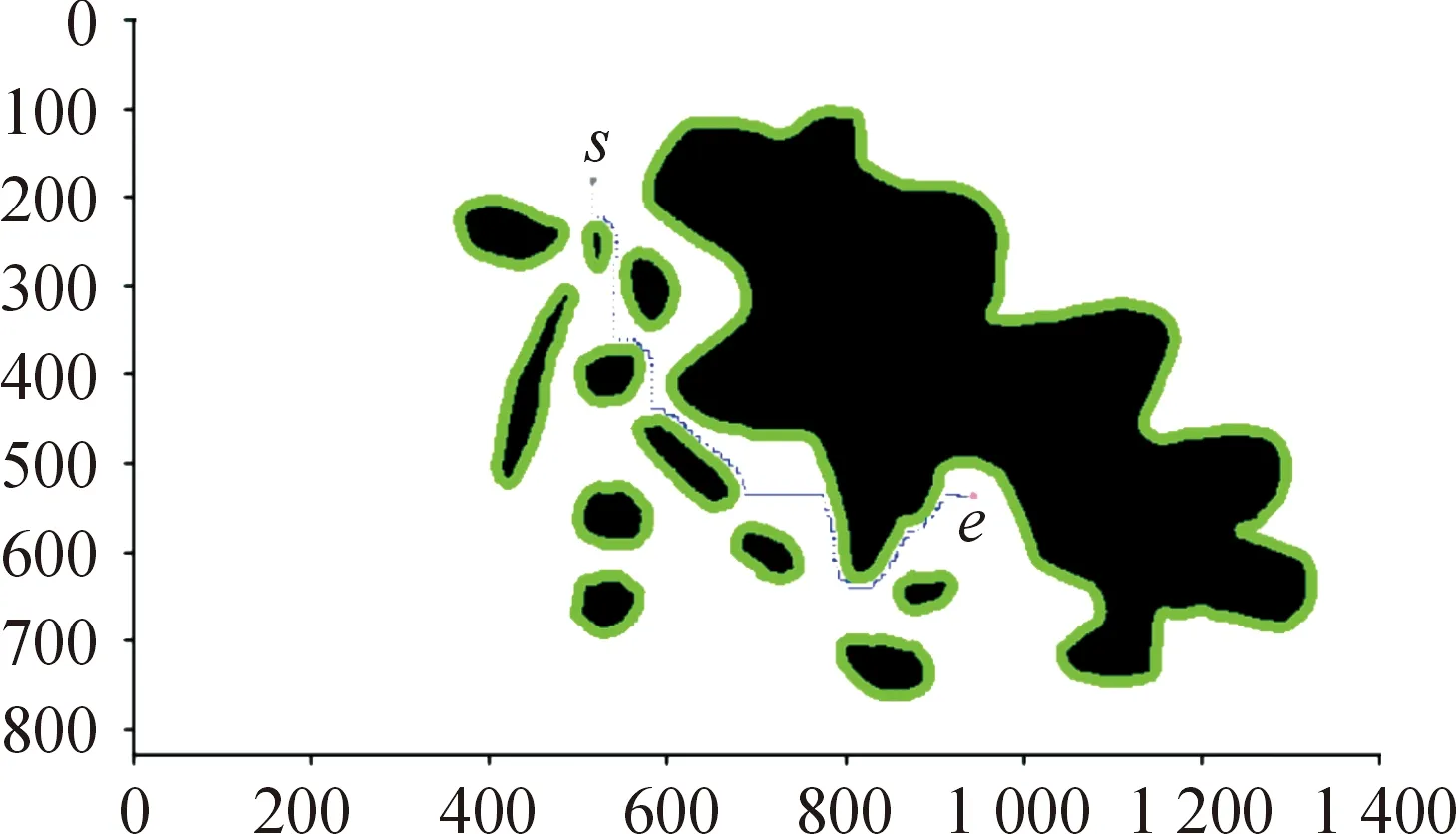
图4 变向干扰值优化的路径示意图

路径平滑优化

在引入变向干扰值约束后，可以获得变向较少的路径，但是此时获得的路径中还存在一些变向角度过大的拐点，并不符合无人船的运动规则。需要将这些拐点拟合成一条平滑的曲线。这里用贝塞尔曲线进行路径平滑优化，贝塞尔曲线公式如下：

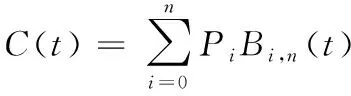
(8)

(9)

(10)

假设一条路径有+1个节点，，…,，利用阶贝塞尔曲线优化得到如图5所示的平滑曲线。

图5 贝塞尔曲线优化的平滑曲线

3 多路径搜索算法

经过基于改进A算法的路径搜索后，便得到一条优化路径，但是由于A算法不能保证一次搜索得到的路径就是最优路径。为了能够获得多条平衡了路径相似度和路径航行代价的优化路径，提出一种多路径搜索算法。

首先利用改进A算法进行路径规划搜索出一条优化路径，将该路径上的所有节点坐标和航行代价存储起来，并提高其移动到终点的估算成本，结合式(7)，新的代价函数为

()=()+*′()+()

(11)

当为存储节点时，′()=()。为新节点时，′()=()，为成本倍数系数。

再次利用改进A算法进行搜寻，由于搜索过的路径上的节点到终点的估算成本提高，再次搜索得到的路径便是平衡了路径相似度和路径航行代价的优化路径。

多路径规划算法流程如图6所示。

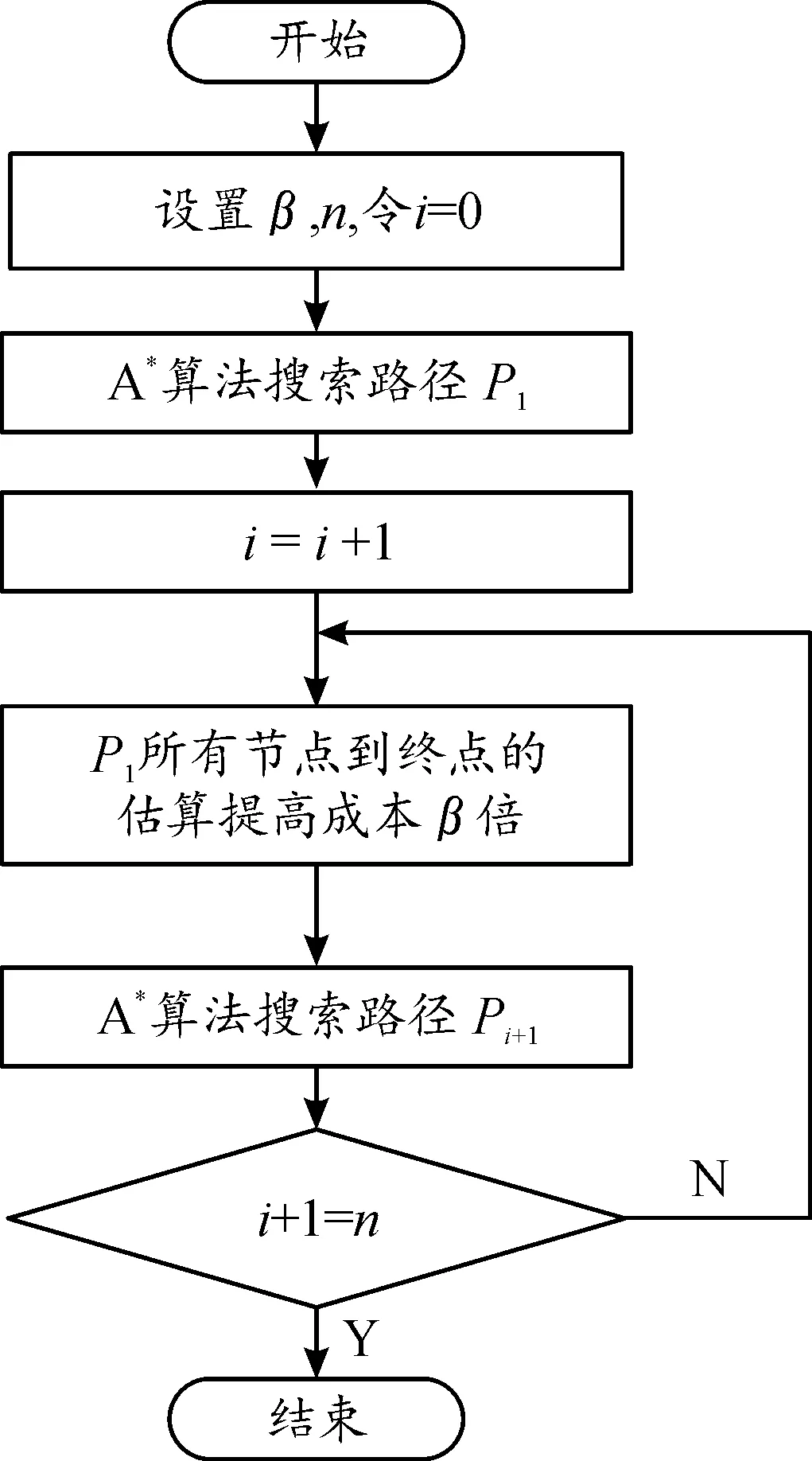
图6 多路径搜索算法流程框图

设置=15，=2时，可以得到两条优化路径，如图7所示。

图7 多路径搜索优化路径示意图

多路径优化算法通过对已搜索路径的航行代价加权搜索新路径，相比于传统A算法，缩小了搜索范围，提高了搜索效率。传统A算法搜索范围如图8中橙色区域所示，基于人工势场的改进A算法搜索范围如图9中橙色区域所示，优化算法搜索范围如图10中橙色区域所示。

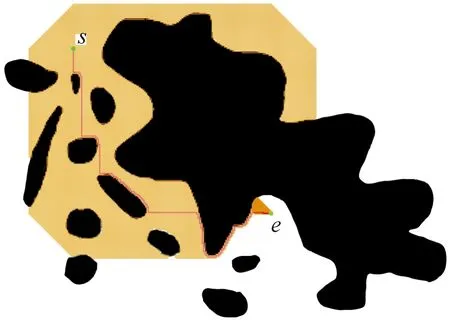
图8 传统A*算法搜索范围示意图

图9 基于人工势场的改进A*算法搜索范围示意图

图10 优化算法搜索范围示意图

4 风险评估函数

无人船的实时传感器难以检测到被遮挡视野的障碍物。如图11所示，无人船在栅格地图中有2种风险区域，绿色区域为靠近障碍物的风险区域。红色圆圈区域为存在双重碰撞几率的高风险区域，这里视野受到遮挡，环境复杂，碰撞风险大。

图11 风险区域示意图

因此，通过多路径搜索算法得到的多条路径虽然航行代价相似却存在不同的风险，需要评估路径的安全性，以获得平衡了航行代价和安全性的全局最优路径。风险评估函数定义为

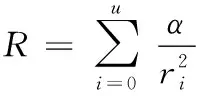
为风险系数，为节点到不同障碍物的距离，风险等级的范围是(0,),为周围障碍物的数量，障碍物越密集的地方，其风险等级也越高。

当=1，>时，<1,为障碍干扰值的覆盖宽度。表示该区域远离障碍物，风险等级较低。

当>1,>1时，表示该区域为高风险区域，障碍物密集。

利用风险评估函数对搜索到的所有优化路径进行风险区域检测，通过比较路径经过高风险等级区域的数量，便可以获得全局最优路径。

5 仿真结果

在 Python 3.7环境下，为验证风险因素影响下无人船智能路径规划方法的可行性，对某海域的电子海图进行栅格化处理，设置每个栅格代表的横向与纵向实际距离均为 20 m，处理结果如图1所示。然后利用改进A算法进行路径规划搜索出一条优化路径，如图5所示。设置=15，=2，得到优化路径1和优化路径2，如图12所示。

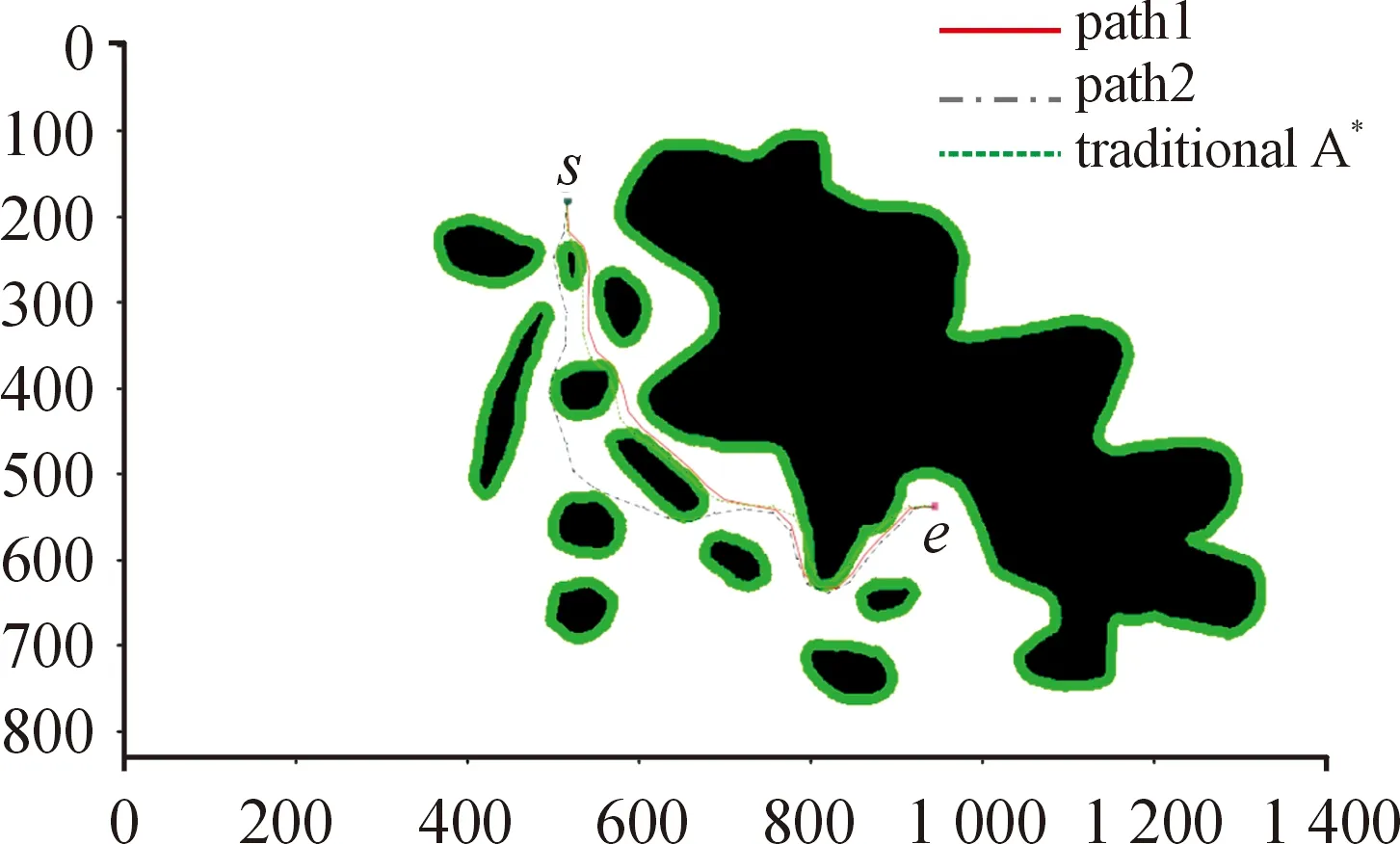
图12 传统A*路径和优化路径示意图

对比传统A算法搜索的路径，和利用多路径搜索获得的两条改进A算法的优化路径，所得结果如表1所示。

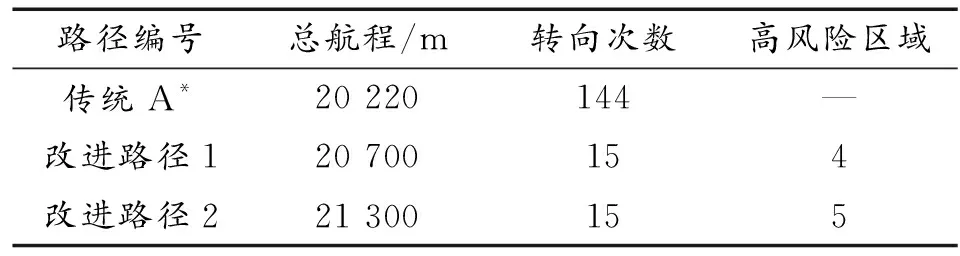
表1 本文中方法与传统方法路径规划结果Table 1 Comparison of path planning performance between this method and traditional method

对比传统A算法、基于人工势场的改进A算法和本文中的优化算法的搜索效率，所得结果如表2所示。

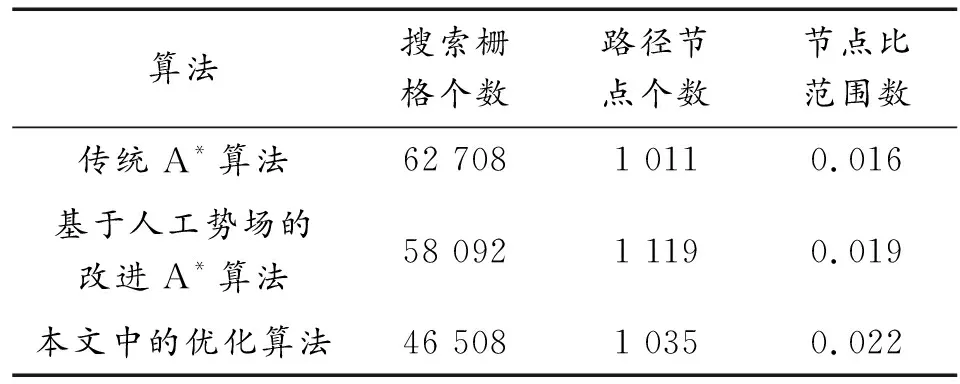
表2 搜索效率Table 2 Comparison of search efficiency

表1可知：本文中的优化算法比传统A算法规划的总航程略长，A算法变向很频繁，本文中的优化算法转向次数比传统A算法明显减少。传统A算法规划的路径一直贴着危险区域，路径1和路径2途径的危险区域明显减少，路径1途径的危险区域最少。表2可知：本文中的优化算法搜索范围比传统A算法和基于人工势场的改进A算法的小，从相同的起点搜索到终点本文中的优化算法搜索效率最高。

综合考虑规划总航程，变向次数和途径风险区域的数量，路径1是全局最优路径。

6 结论

通过改进基于A算法的无人船路径规划，提升了无人船路径规划的实用性和安全性。利用多路径搜索算法可以获得多条协调了航行代价和路径相似度的优化路径。

所提出的风险因素影响下无人船智能路径规划方法可获得平滑度更好、更安全的全局最优路径，非常适用于无人船在复杂海洋环境下的路径规划。