渗透的是思想 孕育的是策略

陈志凤

[摘要]小学数学教材编排是以数学知识的发生、发展、运用为主线，知识内容是显而易见的，但对于数学知识中所蕴含的数形结合思想教材并未明确指出，尤其是在解决问题的策略单元教学中，合理地运用数形结合的思想，有助于化抽象为直观，打破学生的思维局限；有助于学生解决具体的问题；有助于拓展学生寻找解决问题的途径，从而促进学生策略的形成，提高分析问题和解决问题的能力.

[关键词]数形结合思想；有效渗透；策略形成

随着社会的发展，要想实现终身学习和人的可持续发展，在教育中发展学生的能力，使之掌握获得知识和进一步学习的方法，逐渐掌握蕴涵在知识内的思想和方法也就显得尤为重要，小学数学涉及的数学思想有很多，如数形结合思想、函数思想、转化思想、分类讨论思想……用数学思想引领数学课堂，对学生解决问题的策略形成必将有质的提升.小学是学生学习数学知识的启蒙时期，在数学教学中运用数形结合思想，不但符合学生的认知规律，而且能引起学生的学习兴趣，激发学生的学习积极性，提高学生分析问题和解决问题的能力.

小学数学教学中渗透数形结合思想的意义

1.渗透数形结合的思想，培养思维的灵活性和创造性

数形结合具体地说就是将抽象的数学语言与直观图形结合起来，通过“数”与“形”之间的对应和转换来解决数学问题.著名数学家华罗庚指出：“数缺少形时少直观，形少数时难入微.”这句话说明了“数”和“形”是紧密联系的，由数想形，以形助数的数形结合思想在解答问题时，具有可以使问题直观呈现的优点，有利于加深学生对知识的识记和理解；有利于学生分析题中数量之间的关系，丰富表象，引发联想，启迪思维，拓宽思路，迅速找到解决问题的方法，从而提高分析问题和解决问题的能力.它可以借助简单的图形、符号和文字所作的示意图，促进学生形象思维和抽象思维的协调发展，沟通数学知识之间的联系，从复杂的数量关系中凸显最本质的特征，例如，我们常用作线段图、树形图、长方形面积图、集合图、数轴等，帮助学生理解抽象的数量关系、数学概念，使问题简明直观，这些都体现了数形结合的思想，在解决问题的过程中，提高学生的思维能力和数学素养，适时地渗透数形结合的思想，可达到事半功倍的效果.

2.应用数形结合思想，增强思维的广阔性和深刻性

“数形结合”是一种重要的数学思想，对教师来说是一种教学策略，是一种发展性课堂教学手段；对学生来说则又是一种学习方法.数形结合思想形成的前提是让学生经历应用的历练，而教师提供时间与空间是“方法”提升为“思想”的保证，如果长期渗透，运用恰当，则使学生形成良好的数学意识和思想，长期稳定地作用于学生的数学学习生涯中.在教学中，教师应充分利用学生形象思维的特点大量地用“形”解释、演示，帮助理解抽象的“数”.

数形结合思想在解决问题的策略教学中的渗透与应用

苏教版数学教材从第二学段开始，每册编排了一个“解决问题的策略”单元，依次介绍了列表、画图、一一列举、转化、假设等解决问题的基本策略.“形成解决问题的一些基本策略，体验解决问题策略的多样性，发展实践能力和创新精神”是《数学课程标准（2011版）》确定的课程目标之一，教材编写“解决问题的策略”这样的单元，就是为了贯彻落实这样的课程目标.解决问题的策略是在长期数学教学中不断培养的，是通过各个领域内容的教学逐渐形成的，单独编写“解决问题的策略”这样的单元，能加强策略的形成和对策略的体验.怎样在教学中渗透基本的数学思想，帮助学生提高解决问题的能力，形成解决问题的一些基本策略，一直是值得每位教师认真思考的问题.本文结合笔者执教的三次“解决问题的策略”的课例，就数形结合的思想方法在“解决问题的策略”单元教学中的有效应用谈谈自己的认识.

1.数形结合：化抽象为直观，打破学生思维局限

在中高年级的数学教学中，学生在解决有一定思维难度的数学问题时，常常会被题目中繁杂的信息所困扰，不知从何下手，尤其是行程问题和图形的面积变化问题，而画图可以将题目中的信息简洁地表示在图中，学生根据所揭示的数学问题内涵，采用画线段图或面积变化图的方法，把抽象的问题具体化、直观化，从而找到解决问题的突破口，形成解决问题的策略.可见，“画图策略”是解决问题的常用方法，是“数形结合”思想的具体体现，

案例1：苏教版四年级下册《用“画图”的策略解决问题》片段回放：

出示题目1：东关小学有一块长方形试验田.如果这块试验田的长增加6米，或者宽增加4米，面积都比原来增加48平方米，你知道原来试验田的面积是多少平方米吗？

师：怎样理解这道题？（大家互相说一说，讨论一下）

师启发：长增加的时候，宽增加吗？宽增加的时候，长增加吗？

指示学生回答，师总结并出示课件：

如果长增加6米，宽不变，面积比原来增加48平方米；

如果宽增加4米，长不变，面积比原来增加48平方米，

生画图，师指导，突出说明两个增加的部分不能相连， 解答：48÷6=8（米），48÷4=12（米），12x8=96（平方米）.

师总结：通过画图我们把复杂的问题变简单，抽象的文字变直观.这就是画图策略的重要作用.并板书：复杂——简单；抽象——直观.

出示题目2：王营小学原来有一个长方形操场，长50米，宽40米，扩建校园时，操场的长增加了10米，宽增加了8米，操场的面积增加了多少平方米？

学生画图，呈现两种不同情况.

引导学生结合题意进行讨论，师：你们认为哪一种画法符合题目的意思？为什么？（师组织学生讨论，最后得出正确的答案）

学生在解答这个问题时情况也很多，出现了四种不同的解答方法.

通过数形结合（画图），让学生在图中表征题目中的信息，使原本复杂的题意直观化、形象化，打破学生思维的局限性，让解决问题的方法多样化，这样的教学从简单到复杂，层层推进，充分体现了开放性、综合性和应用性.通过两个问题的尝试、比较、探索，学生掌握了解决此类问题的基本方法，形成了画图的基本策略，激发了学习的兴趣，激起了探究的欲望，endprint

‘

2.数形结合：学生解决具体问题的“向导”

在小学数学教学中，恰当地运用数形结合的思想方法，能将抽象的数学语言与直观的图象结合起来，把复杂的问题简单化，抽象的问题形象化，从而较好地突破教学难点，促进学生的数学学习，

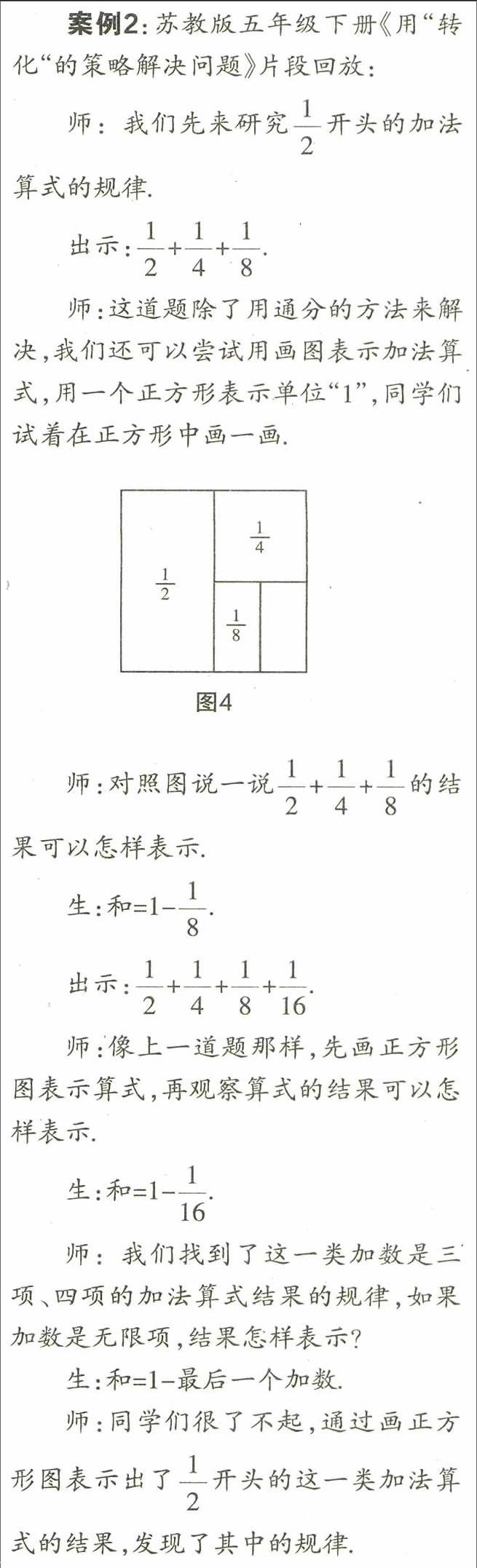
案例2：苏教版五年级下册《用“转化“的策略解决问题》片段回放：

师：我们先来研究 开头的加法算式的规律.

出示：

师：这道题除了用通分的方法来解决，我们还可以尝试用画图表示加法算式，用一个正方形表示单位“1”，同学们试着在正方形中画一画.

本节课的教学目标之一是让学生经历有序的探究过程，体验数学规律的形成过程，感悟探究数学规律的一般方法.教师在呈现问题时也很有序，先研究加数是三项，再研究四项，在此基础上拓展到无限项，符合学生的认知逻辑.这个过程能让学生初步体会到用直观的“形”表示抽象的“式”二者的和谐统一，从而使问题得以巧妙地解决.

3.数形结合：拓展学生寻找解决问题的途径

运用数形结合有时能使数量之间的内在联系变得比较直观，成为解决问题的有效方法之一.在分析问题的过程中，注意把数和形结合起来考察，根据问题的具体情形，把图形的问题转化为数量关系的问题，或者把数量关系的问题转化为图形的问题，使复杂问题简单化，抽象问题具体化，化难为易，

案例3：苏教版六年级下册《解决问题的策略》片段回放：

出示题目：全班42人去公园划船，租10只船正好坐满.每只大船坐5人，每只小船坐3人.租的大船、小船各有多少只？

应该给学生足够的时间思考：解决这个问题，你准备选择什么策略？

生1：画图：先画10只大船坐50人，再去掉多的8人

生2：一一列举：从大船有9只、小船有1只开始，有序列举，

生3：假设：假设大船和小船同样多，再根据总人数调整，

在上面这个片段中，数形结合很好地促进学生联系实际，灵活解决数学问题，而且还有效地防止了学生的生搬硬套，打开了学生的解题思路，由不会解答到用多种方法解答，逐步让学生感悟到了不同策略中的共有规律，引发了学生的创新思路，它将学生头脑中原有的思维方式进行了更新，拓展了学生寻找解决问题的途径，从而提高了解决数学问题的能力.endprint