倾听学生——初中数学把握学情的重要途径
陈卓
[摘要]初中数学教学中要落实“以生为本,以学定教”的先进教学理念,其基础是对学生学情的准确把握,把握学生学情的途径很多,但从时效性上来看,倾听学生是即时把握学生学情的最为有效的途径.倾听学生的前提是学生敢于、善于表达,而这需要教师赋予学生安全的学习心理环境,并且引导学生克服虚荣心理,不怕出错;倾听学生的关键在于根据学生的表达,准确地判断出学生在数学思维上出现的问题,倾听学生还需要及时向学生反馈所获得的信息,以从智力因素和非智力因素两个方面促进学生的发展,
[关键词]倾听;学情;初中数学
“以生为本,以学定教”这一先进教学理念应当如何理解?笔者是这样理解的:教学中要以学生为根本(学生主体、教师主导也有类似的含义),根据学生学的情况来确定教师的教,基于这样的理解会发现,了解学生的具体情况,是这一教学理念落到实处的关键所在,而这恰恰就是传统教学中所强调的对学情的把握.那么,如何才能有效地把握学情呢?根据教学经验可以知道,通过学生作业得到的反馈,通过调查研究得到的反馈,都是掌握学情的有效途径,但如果要即时了解学生的学习情况,并对自身的教学作出适当的调整,那就必须采用现场研究的方法,笔者提出的思路是:倾听学生!
倾听学生常常被当成一种具有浪漫意味的教学表述,笔者从事初中数学教学,浪漫不起来,却能够从理性的角度来看待这一教学方式,倾听学生无非是通过学生的口头描述去知道学生在学习过程中是怎么想的.倾听学生很简单,只要教师给自己足够的耐心即可;但倾听学生却有一个重要的前提,那就是学生愿意表达,只有学生愿意表达、准确表达,教师所获得的信息才具有参考的意义.笔者结合自身在教学中的一些努力与实践,谈一谈笔者是如何通过倾听学生来有效地把握学情的.
学会表达——倾听学生的重要基础
有经验的教师会发现,今天的初中学生越来越不会表达了,一方面有学生学习心理方面的原因,他们的自尊心导致了一种自我保护意识,而自我保护的结果就是在课堂上“沉默是金”.初中数学不同于小学数学,其丰富的知识量加上较高的逻辑思维要求,使得相当一部分学生害怕表达时出错,因而不愿表达,时间一长,导致的结果就是不会表达.而倾听学生又离不开学生的准确表达,那么如何化解这个难题呢?笔者以为可以从两个方面来进行:
第一,给学生营造一个安全的学习心理环境,由于数学学科是相对理性的学科,因此数学教师常常以严肃的面貌出现在学生的面前,加上上面提到的学生的自尊心理,因此数学课堂上学生表达确非易事,要让学生有效表达,首先要让学生感觉到在数学课堂上说错了也没有关系,问题在于,只跟学生说这一点是没有作用的,教师要通过自身的教学行为,让学生切实感受到这一点.记得笔者在教授“最短路径问题”(人教版初中数学八年级上册)的时候,选择了教材上的一道例题:牧马人从A地出发,到一条笔直的河边Z饮马,然后回到B地,牧马人到河边的什么地方饮马,可使所走的路径最短?在解决这个问题的时候,笔者假装出错:选择了,A和B两点连线的中点,然后作出A和B分别与l的垂线,再过中点作出中位线,与l的交点则为寻找到的最短路径的点.嘴里还一边嘀咕:选两点的中间,大家公平,应该是最短路径的点.聪明的学生就会发现这个方法有问题,由于他们的学习心理相对理想,因而敢于指出教师存在的错误,这个时候教师假装不好意思,从而引得其他所有的学生放下戒备心理.事实证明,这样的方式在化解学生害怕出错的心理上屡试屡成,
第二,让学生学会用数学语言进行表达.在学生敢于表达之后,要引导学生学会表达,就数学学习而言,所谓学会表达,就是学会用数学语言进行表达.事实上在上面的实例中,教师要引导学生用数学语言如此表达:最短路径实际上就是在Z上找一个点C,使AC+BC的距离最短,这样的表述是纯粹数学化的,饮马问题便成为数学问题.这里还需要进行一个数学转换:假如A,B两点分别位于l的两侧,则C点又应当如何确定?在进行了这一转换之后,学生自然就会思考:这样的转换与原问题有什么不同?于是寻找原问题中A或B点关于l的对称点就成为数学表达的最重要的一句话,
总之,只要学生敢于、善于用数学语言进行表达,教师的倾听就有了坚实的基础.
善于倾听—一了解学情的重要途径
在初中数学课堂上,教师善于倾听总体现为教师对学生错误思路的判断与分析,因为当学生表达正确时,学生对数学知识的构建往往是有效的,那就达到了教师的教学目标,不需要太多的关注(学生的创新思维所导致的数学表达除外);而当学生表达出错的时候,就需要教师能够即时判断了,
比如说在教“因式分解”的时候,不少学生对于把一个多项式写成几个整式的乘积感到困难,而且学生出错的原因又是多方面的,因此就需要教师善于倾听学生的表达,并把握学生的思维错在何处,如将8a3b2+12a2b3分解因式时,有学生就会得出这样的结果:8a3b2+12a2b3=4ab(a2b +abz),当教师追问学生时,学生仍然认为这是最简的结果.那么此时学生是怎么想的呢?问了之后学生回答:a2b和ab2一个是a的平方,一个是b的平方,不好再分解了.听懂了吗?在这个学生的思维当中,由于平方出现的位置不一样,因此在他的眼中就已经是最简形式了.而这样的思维与教师所期待的显然是不一致的,如果不加以追问,甚至会责怪学生这么简单的东西都出错.而一听之下则知道了学生原来是在对a2b和ab2的公因式判断上出了问题.而知道了这一点,教师要做的就不是责怪学生,而是进一步跟学生强调公因式的含义即可.
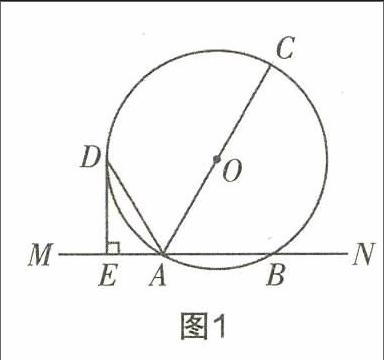
当然,这是新知学习中的一个常见错误,如果到了中考复习期间,学生会在一些更为复杂的数学问题上出错,这个时候就更需要教师倾听学生,以了解学生的思路了.譬如一道中考原题:如图1,直线MN交⊙0于A,B两点,AC是直径,AD平分∠CAM交oo于D,过D作DE⊥MN于E.(1)求证:DE是⊙0的切线;(2)若DE=6cm,AE=3cm,求⊙O的半径,endprint
有学生在解决这道题时感觉无法下手,这是初中数学教学中比较头疼的一种现象,无法下手往往意味着思路的混乱,可是学生为什么会思路混乱呢?还是只能通过倾听学生去知道原因.在引导学生阐述的时候,有学生这样说:切线不是作出来的吗?怎么还需要证明DE是⊙o的切线呢?笔者一听这话就知道了这位学生对切线的理解是生硬的,他只知道切线是作出的与圆只有一个交点的直线,而没有意识到证明一条线是圆的切线,可以通过切线的判定方法去进行;还有基础较好的学生说:我想不到圆的半径与给出的已知量有什么关系,这样的一句话,可以让教师判断出这位学生对本题的理解比较肤浅,他看不出直角三角形ADE以及三角形ACD与三角形ADE的相似关系能够发挥的作用.再进一步讲,这类学生在思维的深刻性以及逻辑性上有薄弱的地方,他们不善于进行复杂的推理,因此,对于这类学生的教学重点,就是通过一定难度的题目去循序渐进地培养他们的思维能力,应当说,这些教学判断,都是基于倾听学生得来的!
及时反馈——倾听学生的价值所在
倾听学生是一个单向的过程,是学生的学情向教师传递的过程.事实上,倾听学生之后还需要反馈给学生,以提升学生数学学习的策略性知识,而在这种反馈的过程中,教师又可以倾听到更多的东西.
譬如对部分数学尖子生的培养,就需要利用课余的时间跟学生交流,以在倾听学生的同时给他们反馈积极的信息,笔者倾听的结果表明,数学尖子生一般对自己的数学学习往往有特殊的要求,他们常常不满足于教师一般的讲授,他们需要教师给他们提供高精尖的题目,在知道了这一点之后,笔者也反馈给他们一些有益的信息,比如说数学学习既需要研究有一定难度的题目,也需要夯好基础,练好基本功——这一点其实点出了部分尖子生在数学学习中的不足:他们热衷于攻克难题,但在解决难题的过程中,常常会出现表达不清晰的情况.而这样的反馈信息也常常会被这些学生所接受,更重要的是,教师的及时反馈往往是基于他们的实际学习情况,有时他们自己意识不到,有时虽然有意识但意识不清晰,因此教师此时的倾听与反馈,对于这些学生来说就是学习力的提升过程,对于学困生也是如此,倾听与反馈可以让他们知道自己学习上的不足,而教师对学困生反馈信息,又应当从智力因素和非智力因素两个方面人手,关于这一点,相信大多数同行都有经验,故不再赘述,
综上所述,初中数学教学中,教师要多倾听学生,以切实把握学生的学习思维,以为自己进行更为有效的数学教学设计及课堂教学奠定基础.endprint

