遗传关联性研究Meta分析的多重检验校正方法
翁鸿,张永刚,牛玉明,曾宪涛
· 循证理论与实践 ·
遗传关联性研究Meta分析的多重检验校正方法
翁鸿1,2,张永刚3,牛玉明4,曾宪涛1,2
制作遗传关联性研究Meta分析时,我们常常计算其五个基因模型的结果,而这一做法使得检验次数增多,增大了假阳性结果的发生率。此外,也有研究在同一研究中对多个位点、多种表型进行分析,这也会增加假阳性结果的发生率。因此,在制作遗传关联性研究Meta分析时,除了计算出每个基因模型的结果外,还应给出每个基因模型检验结果的校正值,判断结果是否为假阳性结果。本文主要介绍多重检验校正的方法。
遗传关联性研究;多重检验;校正;Meta分析
在制作遗传关联性研究Meta分析(尤其是候选基因研究的Meta分析)时,多数研究者会采用计算五种基因遗传模型的结果(即同时进行五个假设检验);也有研究者在同一个研究中研究多个遗传位点、多种表型,这也增加了假设检验的数量;此外,在全基因组关联性研究及其Meta分析中,假设检验的个数更为庞大。在不调整检验水准的情况下,随着检验次数的增加,假阳性错误的发生率也会随之增加。因此,在制作遗传关联性研究Meta分析时,除了计算出每个基因模型的结果外,还应给出每个基因模型检验结果的校正值,判断结果是否为假阳性结果。本文主要就多重检验校正的方法进行阐述,方便读者在制作遗传关联性研究Meta分析时合理应用这些校正方法。
1 经典假设
典型的假设检验过程是,先假定零假设(H0)和备择假设(H1),再计算统计量(T),通过T来判断是否拒绝H0。关联研究中H0指效应值等于0,H1指效应值大于1,因此,在病例对照研究的遗传关联性研究中,将比值比(odds ratio,OR)的对数值logOR作为效应值。此时,P值的定义为假设H0为真时,出现T及大于T数值的概率。公式如下:
P=P(T≥t|H0)
若P值小于预定的显著性水平α=0.05,则拒绝H0,即有统计学意义。
2 多重检验
多重检验就是对多个假设同时进行检验。多重检验的主要问题是,当一个研究中同时进行多个假设检验时,将假设检验显著性水准设定为α=0.05可能会增加假阳性结果的发生(即Ⅰ型错误的发生率增加),如下:
Ⅰ类错误:
第一次,α=0.05
第二次,1-(1-α)2=0.0975
…
第n次:1-(1-α)n
因此,涉及到多个基因、多个位点、多种表型或疾病的遗传关联性研究及其Meta分析均需进行多重检验的校正。
3 多重检验的校正方法
多重检验的校正方法主要有控制总Ⅰ型错误率(FWER)、对预设定的显著性阈值进行Bayesian分析、错误发现率(FDR)法、FDR改进的方法及假阳性结果报告率(FPRP)法。控制FWER的方法有Bonferroni校正、递减Bonferroni校正及置换检验。
3.1 Bonferroni校正Bonferroni校正常用于多重检验的数量级较为适中的情况,且各检验之间的依赖性较弱,若同一研究中的多个遗传突变的联系较为紧密,此时不宜使用Bonferroni校正法。Bonferroni校正法基于检验的个数[1],简单地增加显著性水平,对m个假设检验,采用Bonferroni校正法后,显著性水平α′为0.05/m:
0.05 =P(Pmin≤α|H0)=1-P[(P1>α)∩(P2>α)∩…∩(Pn>α)]=1-(1-α)m
Pmin为最小P值,解上述方程,得出α=1-(1-0.05)1/m≈0.05/m。例如,一个遗传关联性研究Meta分析检验了五种基因模型,那么校正后的显著性水平α'=0.05/5=0.01,即将各基因模型所得检验结果P值与0.01进行比较,而不再是与0.05。但遗传关联性研究Meta分析的各基因模型之间并不十分独立,也存在某种关系,此外,这种方法过于保守,有校正过度的可能[2](即可能会增加假阴性的发生率)。因此,该方法并不十分适用于遗传关联性研究Meta分析结果的校正,但由于保守,可以最大限度的控制假阳性结果,该方法被用于全基因组关联研究的显著性水平的设定(α=5×10-7)[2]。
3.2 递减Bonferroni校正递减Bonferroni法也称为Step-down Bonferroni法或Step-down Holm法,最早由Holm提出[3],由Shaffer[4]进一步改进,其后Holland[5]又将该程序进行了优化,增强了该方法的检验效能。该方法通过原始P值进行排序,排序顺序为按P值的大小,设n为对应P值的序号,然后根据PAdjust=(m-n+1)×P公式计算校正后的P值(PAdjust),然后将校正后的P值PAdjust与0.05进行比较,若PAdjust小于0.05,则认为具有统计学意义,即该遗传位点突变与疾病有关联。
3.3 置换检验该方法的原理是以H0为真的情况作为模板,然后计算出调整后的P值。先对未校正的P值进行排序,然后根据基因之间结构上的关系,多次置换,从而得到Pmin值的经过实证后的虚拟频数分布,将从实际数据中得到的P值与置换后的分布相比,从而得出校正后的PAjust。若进行了x次置换,得到x个Pmin,从实际数据得到的P值比y个Pmin值小,则校正后的Padjust=(y+1)/(x+1)。各检验之间存在依赖关联时,置换检验优于Bonferroni检验,该方法功能较为强大,但其计算量较大(置换次数一般为1000次),增加了普及和使用的难度。也有研究者提出减少其计算难度的方法,如通过模拟或者将实证分布与分析分布进行拟合[6]。
3.4 Bayesian分析法从统计学角度来说,P值本身并不能说明H0为真的可能性有多大[7]。因此,Bayesian理论可以用来评估某一检验H0为真的概率的大小,其公式如下:

其中(1-β)为统计效能,π为H0为真的先验概率,P("H0" |"p≤α" )为该检验有统计学意义时假阳性的概率。上述等式等价于:
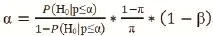
根据上述等式可以发现,当H0与H1出现的概率相同(即π≈0.5),且统计效能较高(1-β≈1)时,假阳性概率≈α,而我们通常将α设定为0.05,因此,上述等式为α设定为0.05提供了一定的理由。另一方面,当(1-β)较小,即研究效能不足时,为了使假阳性概率不变,α必须按比例降低。
3.5 FDR法FDR法由Benjamin和Hochberg提出[8],故又称为BH法。假设同时对m个假设进行检验,其中有m0个假设是正确的,m1个假设是错误的,对m个假设检验完成后,被拒绝的零假设个数记为R,被接受的零假设个数为W。如表1所示,假设检验的个数m是已知的,被拒绝的零假设个数R是可观测的随机变量,而U、V、S、T四个变量是不可观测的随机变量。

表1 m个检验的假设检验结果
根据表1,FDR的定义如下:

FDR法是通过控制错误发现率来进行P值调整。FDR设定为0.05,将未校正的P值按从小到大的顺序进行排序,如P1≤P2≤…≤Px≤…≤Pm,Pm为所有未校正P值中最大者,然后选出PAdjust≤(n×0.05)/m的所有情况,并找出其中排序最高的P值(Px,且Px≤Pm),那么认为排序为r以内的检验被认为是具有统计学意义。
3.6 改进FDR法该方法首先同FDR法,先进行P值排序,然后计算PAdjust=mp/r,若第r次序号的Pr大于第r+i(i=1,2,…)次Pr+i时,Pr用Pr+i中最小的值代替[9]。若校正后的PAdjust<0.05,则认为具有统计学意义。此外,FDR法还有较多的改进方法,比如加权FDR法、依赖性检验的FDR法及参数FDR法[7,10,11]等。总之,FDR法较控制FWER法宽松,允许更多的假阳性存在,同时也减少了假阴性的存在[2]。
3.7 FPRP法FPRP法是针对分子流行病学研究而研发出来的[12]。在研究遗传突变与表型或疾病的关联时,传统统计学方法并不关注研究的H0和H1的概率,认为它们是非随机的、未知的,但在研究较多个不确定的位点或单体型时,H0和H1却是有概率性的[13]。因此,尽管是设计较好、样本量较大的遗传关联性研究,也存在较高概率的假阳性结果(≥95%)[14,15]。FPRP法需要用到先验概率,但比Bayesian法更好理解,实际上属于一种Bayesian方法,但又不同于传统的Bayesian法。设H1先验概率为λ,FPRP定义为:

α为显著性水准,(1-β)为统计效能。由上述公式可以看出,FPRP与α、(1-β)及λ有关,且λ是影响FPRP最重要因素,此外,确定λ值也是FPRP法的关键步骤。Wacholder等[12]将FPRP的步骤分为4步:
①预设FPRP临界值。对遗传关联性研究Meta分析而言,FPRP的设定要较为严格,一般设定为0.2;
②确定H1的先验概率λ。精确设定λ值是没有必要的,因此,通常将其分成低(≈0.001)、中(≈0.01)、高(≈0.1)三类;
③确定OR值、遗传模型及统计效能。一般将OR设定为1.5。
④计算FPRP值。根据FPRP定义的公式计算出FPRP值,然后与预设定的FPRP临界值0.2进行比较,若小于临界值,则认为该遗传突变与表型或疾病之间的关联有统计学意义。此外,在进行遗传关联性研究Meta分析的结果校正时,我们可以将H1先验概率λ的三个分类均计算出来,然后进行敏感性分析,综合比较,若计算出来的FPRP值均小于预设定的临界值,则更加增强结果的可信度。
4 小结
控制FWER法依赖于进行检验的数量,因此其逻辑备受诟病,此外控制FWER法较为严格,倾向于引起Ⅱ型错误。FDR法的方法建立的假设基础为:在H0为真时,P值符合(0,1)的均匀分布。但该假设在基因分型偏倚、人群分层级存在相关联的检验统计量时并不成立,此外,FDR法控制的是假阳性的期望比例,并不是真实比例,因此,在遗传关联性研究Meta分析中应用FDR法进行校正,可能会导致误导性的结果。Bayesian法由于其理论较难,推广及普及不易,局限性较为明显。而FPRP法计算较为简单,其理论也不难理解,假设前提不复杂,因此,在遗传关联性研究及其Meta分析中,推荐读者使用FPRP法进行结果的校正。值得注意的是,要明确遗传突变是否与表型或疾病存在真实关联,最主要的方法还是重复进行研究。
[1] 伍小英,鲁婧婧,张晋昕,等. 两两比较的Bonferroni法[J]. 循证医学,2006,6(6):361-3.
[2] 严卫丽. 复杂疾病全基因组关联研究进展——遗传统计分析[J].遗传,2008,30(5):543-9.
[3] Holm S. A simple sequentially rejective multiple test procedure[J]. Scand J Statist,1979,6:65-70.
[4] Shaffer JP. Modified Sequentially Rejective Multiple Test Procedures[J]. Am Stat Assoc,1986,81(395):826-31.
[5] Holland BS,Copenhaver DP. An improved sequentially rejective Bonferroni procedure[J]. Biometrics,1987,43(2):417-23.
[6] Dudbridge F,Koeleman BP. Efficient computation of significance levels for multiple associations in large studies of correlated data, including genomewide association studies[J]. Am J Hum Genet,2004,75(3):424-35.
[7] Al-Chalabi A,Almasy L. Genetics of Complex Human Diseases: A Laboratory Manual[M]. New York: Cold Spring Harbor Laboratory Press,2009.
[8] Benjamini Y,Hochberg Y. Controlling The False Discovery Rate - A Practical And Powerful Approach To Multiple Testing[J]. J R Stat Soc Ser C Appl Stat,1995,57(1):289-300.
[9] 张天嵩,钟文昭,李博. 实用循证医学方法学[M]. 第2版.长沙:中南大学出版社,2015.
[10] Benjamini Y,Hochberg Y. Multiple Hypotheses Testing with Weights[J]. SCAND J Statist,1997,24(3):407-18.
[11] Benjamini Y,Yekutieli D. The control of the false discovery rate in multiple testing under dependency[J]. Ann Statist,2001,29(4):1165-88.
[12] Wacholder S,Chanock S,Garcia-Closas M,et al. Assessing the probability that a positive report is false: an approach for molecular epidemiology studies[J]. J Natl Cancer Inst,2004,96(6):434-42.
[13] 余灿清,李立明. 假阳性结果报告率在分子流行病学研究中的应用[J]. 中华预防医学杂志,2009,43(12):1141-2.
[14] Sterne JA,Davey SG. Sifting the evidence-what's wrong with significance tests?[J]. BMJ,2001,322(7280):226-31.
[15] Colhoun HM,McKeigue PM,Davey SG. Problems of reporting genetic associations with complex outcomes[J]. Lancet,2003,361(9360):865-72.
本文编辑:姚雪莉
Methods of multiple testing adjustments in Meta-analysis of genetic association study
WENG Hong*, ZHANG Yong-gang, NIU Yu-ming, ZENG Xian-tao.*Center for Evidence-Based and Translational Medicine, Zhongnan Hospital of Wuhan University, Wuhan 430071, China. Corresponding author: ZENG Xian-tao, E-mail: zengxiantao1128@163.com
There are five genetic models commonly calculated when the Meta-analysis of genetic association study is performed, which could increase the times of statistical tests and probability of false-positive results. In addition, there are multiple loci and multiple phenotypes analyzed in a study, which also could increase the probability of false-positive results. Therefore, the corrected value of test results of each genetic model should be given besides of calculating the result of each genetic model for justifying the results whether are false-positive results when performing a Meta-analysis of genetic association study. The aim of this study is to introduce the adjustment methods of multiple tests.
Genetic association study; Multiple tests; Adjustment; Meta-analysis
R4
A
1674-4055(2016)12-1409-03
国家重点研发计划专项基金(2016YFC0106300)
1430071 武汉,武汉大学中南医院循证与转化医学中心;2430071 武汉,武汉大学循证与转化医学中心;3610041 成都,四川大学华西医院期刊社;4442000 十堰,十堰市太和医院(湖北医药学院附属医院)循证医学与临床研究中心
曾宪涛,E-mail:zengxiantao1128@163.com
10.3969/j.issn.1674-4055.2016.12.01

