Meta分析中缺失数据的处理方法简介

喻亚宇，许杨鹏，何倩，吴君怡，付文杰，陶圆，张超

· 循证理论与实践·论著 ·

Meta分析中缺失数据的处理方法简介

喻亚宇1,2，许杨鹏1,2，何倩1,2，吴君怡1,2，付文杰1,2，陶圆1,3，张超1

临床试验设计之初，乃至中后期对数据追踪与随访，都可能无法避免部分数据丢失。然而当缺失数据与研究结果可能存在联系时，可能会导致随机对照试验（RCT）偏倚，并且偏倚风险也将被引入到Meta分析结果中。由于缺失数据的情况是非常复杂的，所以对于缺失数据处理要根据实际情况来选择合适的方法。本文就随机缺失、完全随机缺失、非随机缺失的数据缺失机制及其常见的处理方法给出相关简介。

缺失数据；完整案例分析；末次观察推进法；估算个案分析

临床试验设计之初，乃至中后期对数据追踪与随访，都可能无法避免部分数据丢失。在最近的一项对五大医学期刊调查显示，87%已发表的临床试验报告了结局指标缺失[1]。当缺失数据与研究结果可能存在联系时，这可能会导致随机对照试验（RCT）偏倚，偏倚风险也将可能被引入到Meta分析结果当中。推荐分级的评价、制定与评估系统中判断合并效应量的可信度时，也强调充分考虑到缺失值相关偏倚风险[2]。Cochrane手册和系统评价和Meta分析优先报告条目（PRISMA）中均建议系统评价/Meta分析制作者就如何描述如何评估与缺失值相关的偏倚风险给出说明[3,4]。随着意向性治疗（ITT）原则在临床试验中被广泛认可，如果部分数据缺失，则无法得到一个纯粹的ITT分析。目前已有许多研究就如何处理ITT分析中的数据缺失进行讨论[5,6]。本文就缺失数据机制及常见的处理方法给出相关简介。

1 缺失数据的机制

关于缺失数据的讨论首要考虑的是数据缺失的原因，可能由于与试验无关的原因缺失，如参与者因车祸死亡而无法参与试验。也可能由于与试验相关的原因而缺失，如使用安慰剂的参与者可能因治疗无效而退出。数据缺失的原因在如何处理数据缺失时有重要作用。缺失数据的研究分析包括参与者提前退出试验的原因，错误假设会导致潜在偏倚效应量，为了对缺失数据采取合适的处理，我们需要了解缺失数据的机制。Rubin和Rubin对于缺失数据分类有明确定义[7]，这种分类方法取决于数据缺失原因。Little and Rubin机制包含以下三个类型：

1.1 随机缺失（MAR）在MAR假设下，数据缺失原因取决于完全观测到的协变量（如干预、基线），而与未观测到的因素无关。如假设小学生被随机分配到不同的干预组为了降低学生在学校的焦虑，通过症状严重程度量表测量，低龄学生可能更难收集到数据，因为他们很难理解症状严重程度量表。研究中，低龄学生缺失数据的比例与干预措施相关，MAR假设意味着低龄儿童中中途退出者与完成试验者最终结果相似，在MAR假设中，尽管缺失数据与参与者或研究人员有一定联系，但缺失数据不取决于实际结果[8]。统计学分析通常假设缺失数据为MAR，如果假设是正确的，仅分析完整的数据可以得到一个无偏倚的疗效估计[9]。

1.2 完全随机缺失（MCAR） 在MCAR假设下，数据缺失的原因与观测到的变量和未观测到的变量无关，这意味着数据缺失的原因与这项试验无关，所有参与试验的个体数据缺失的几率都是相同的，我们假设研究中缺失数据与完整数据分布规律是一致的，干预措施对于缺失数据和完整数据影响一致，例如：参与者因为车祸中途退出而没有通知研究人员，这样的缺失即为完全随机缺失。因为参与者之间没有存在系统性差异，因此MCAR不会导致疗效结果偏倚[10]。

1.3 非随机缺失（MNAR） 在MNAR假设下，数据缺失与观测到或未观测到的变量或结果有关，参与者中途退出试验的原因可能与干预措施有关，例如：精神病试验中，安慰剂组比抗精神病药组退出率要高，因为安慰剂没有改善患者健康状况。在MNAR情况下，对于完成试验的参与者进行分析时，应该提供一个关于相对疗效的偏差估计，当缺失数据是MCAR或MAR时，偏差估计可以忽略的，当缺失数据是MNAR时，偏差估计是不可忽略的[11]。

2 缺失数据处理方法

2.1 完整案例分析（CC） 完整案例分析法是在Meta分析中最普遍和常用的缺失数据处理方法，在每个研究中，只有完成研究的个体可以被纳入。这种方法要求缺失数据是可忽略的（MCAR或MAR），否则，这种方法会导致偏差估计，如果数据是完全随机缺失，采用完整案例分析则会得到一个无偏倚结果，当数据是非随机缺失时，缺失数据比例越大，此项分析的研究结果就越不可信[12]。像完整案例分析这样完全忽略缺失数据的方法，会降低结果的精准度和研究的统计学功效，而且这种方法违背了ITT分析基本原则。如以下森林图（图1），所采用的数据来自于ACA方法估计。

2.2 末次观察推进法（LOCF） LOCF广泛应用于纵向研究缺失数据处理，这种方法可以用于参与者在试验结束前退出，但是提供了一个或多个中间观测值。该方法以参与者退出前最后一次观测值代替缺失最终结果，LOCF假设了参与者退出试验后最后得到的观测值是典型的并且退出后情况没有发生改变。在每个随机组中，未观测到的最终值的均值等于中途退出者末次观察值的均值[13]。这种方法允许了所有个体被包含在分析之中，符合ITT原则。如果在中途有疗效而在结果没有疗效，则LOCF所估测结果会夸大实际疗效，反之亦然。如果未观测到结果随着时间改善了，则LOCF趋向于更少中途退出者的治疗组；如果未观测到的结果随着时间恶化，则LOCF趋向于更多中途退出者的治疗组[13]。对于LOCF适用的缺失机制尚有争议，有人认为使用这种方法需要数据为MCAR[14,15]，而有人则认为不需要。

2.3 估算个案分析（ICA） 这种方法是假设缺失值的参与人员从未离开过试验，根据缺失值在试验组和对照组干预中不同情况来进行分析，最常用的结局假设如下：

ICA-0：假设所有缺失参与者在两个干预中都没有经历这个事件。

ICA-1：假设所有缺失参与者在两个干预中都经历了这个事件。

ICA-b（best case scenario）：假设所有在试验干预组的缺失患者经历了事件，反之所有在对照组的缺失患者没有经历事件。

ICA-w（worst case scenario）：假设所有在试验干预组的缺失患者没有经历事件，反之所有在对照组的缺失患者经历了事件。

ICA-p：假设对照组中缺失值事件风险与已观测到的一致，试验组中缺失值事件风险与已观测到的一致。这种方法相当于MAR假设。这种效果估计与ACA相同。对每个假设都实施了Meta分析。Meta分析效应量范围反应了结论稳定性和MAR相关性，不一致的结果则指示缺失数据是MNAR。

ICA-pc：假设所有缺失值与对照组中已观测到的参与者有相同的事件风险。

ICA-pe：假设所有缺失值与试验组中已观测到的参与者有相同的事件风险。

以上方法皆可在Stata中使用metamiss命令完成[16]。Higgins，White和 Wood于2008年为这种方法定义，如果假设是合理的，则得到一个无偏倚结果[17]。这种方法主要优点是保留了原始随机化患者，ICA方法倾向于提高“精度”，可以限制它假设结果估算值作为观察值，它忽略了这些估算值的不确定性，然而忽略估算值的不确定性时必须要小心不能低估了标准误[12]。最后，这种方法另一个需要注意的是，只有数量有限的假设通常应用敏感性分析。

3 使用模拟数据阐述处理缺失数据的方法与结果比较

模拟数据基于Cochrane协作网内关于氟哌啶醇和安慰剂治疗精神病疗效比较[18]。选取了其中17项RCT结果作为模拟数据，假定所有缺失数据都为MCAR。使用以上几种缺失数据处理方法对模拟数据进行处理，然后对各种方法处理后合并结果进行汇总比较，结果见图2。

经ACA方法处理后结果（图1）与ICA-p相同，ICA-b、ICA-w与ICA-1、ICA-0提供了两个极端值，ICA-b假设所有缺失值在试验组中都是有利结局而在对照组中都是不利结局，而ICA-w则与之相反，这两种估计提供了与观测值相匹配的最大和最小的效果估计，真实完整的试验结果则在这个区间以内。ICA-1和ICA-0适用于缺失数据结局可以被预测时[17]。例如在戒烟干预中，中途退出者更可能的是继续吸烟[19,20]。图2反应的是各种方法在处理这组缺失数据时的差异，而不是这些方法的优缺点，图2显示ICA-b与其他几组方法间差异巨大，这反映的不是ICA-b的缺点而是对缺失数据结局估计错误。可以看出ICA-1与ICA-pe更适合处理这组模拟数据，即这两种估计更接近缺失数据的真实情况，所得结果更为可靠。

4 讨论

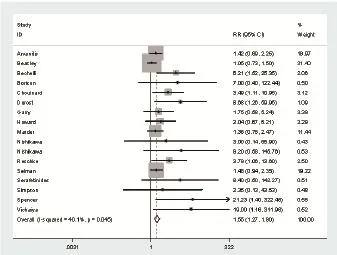
图1 经ACA处理后的结果森林图

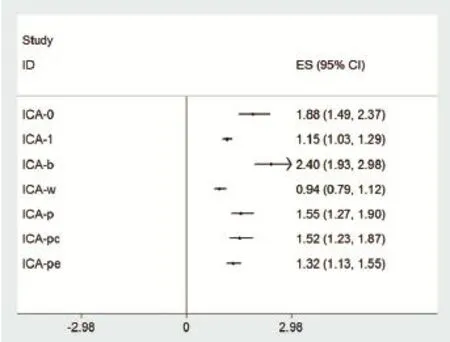
图2 不同假设下处理缺失数据后的结果比较图

缺失数据带来的风险偏倚取决于缺失数据机制，大多数统计学分析假设数据缺失机制为MAR，这种假设是理想化的假设，在缺乏有力的证据时，判断数据缺失的机制可能会引入偏倚。Meta分析通常不具备检测数据缺失原因的能力，仅凭经验性判断数据缺失的原因和机制是不科学的。敏感性分析通常是在不同情况下评估数据缺失机制唯一可行的方法[21]。忽略缺失数据不仅降低了试验统计效能，也会因此引入偏倚，对于缺失数据错误估计则会为研究结果引入更大偏倚。对于任何临床试验和系统评价而言，对于缺失数据处理方法并不是一成不变，而是要根据临床事实与经验做出合理科学的假设然后才能选择合适的方法，例如在精神类试验中，数据缺失原因大都是因为没有疗效或疗效不显著而导致参与者中途退出，对于这类情况选择LOCF可能更为合理。缺失数据的处理难在样本量的限制、RCT的设计、对数据缺失机制的假设以及合适方法的选择。对于处理缺失数据没有最佳方法，最好的方法就是通过制定严密的预案、仔细的收集数据和随访来避免出现缺失数据。同时在缺失数据出现后尽量找到缺失部分，如重新联系到参与者[22]。由于缺失数据的情况是非常复杂的，统计学家不可能设计出一个可以处理所有缺失数据的通用方法，因此对于缺失数据处理要根据实际情况来选择合适的方法，尽可能地降低误差。

[1] Akl EA,Briel M,You JJ,et al. Potential impact on estimated,treatment effects of information lost to follow-up inrandomized controlled trials(LOST-IT):systematic review[J]. BMJ,2012,344:e2809.

[2] Guyatt GH,Oxman AD,Vist G,et al. GRADE guidelines:4.Rating the quality of evidence-study limitations (risk of bias)[J]. J Clin Epidemi ol,2011,64(4):407-15.

[3] J Higgins,SEGreen. The Cochrane Collaboration. Cochrane Handbook for Systematic Reviews of Interventions Version 5.1.0 [updated March 2011]. http://www.cochrane-handbook.org

[4] Moher D,Liberati A,Tetzlaff J,et al. Preferred reporting items for systematic reviews and meta-analyses: the PRISMA statement[J]. Ann Intern Med,2009,151(4):264-9.

[5] Hollis S,Campbell F. What is meant by intention to treat analysis? Survey of published randomised controlled trials[J]. BMJ,1999,319 (7211):670-4.

[6] ShihW. Problems in dealing with missing data and informative censoring in clinical trials[J]. Curr Control Trials Cardiovasc Med,2002,3(1):4.

[7] Mavridis D,Chaimani A,Efthimiou O,et al. Addressing missing outcome data in meta-analysis[J]. Evid Based Ment Health,2014,17(3):85-9.

[8] Little RJ,Ralph D,Cohen ML,et al. The prevention and treatment of missing data in clinical trials[J]. N Engl J Med,2012,367(14):1355-60.

[9] Groenwold RH,Donders AR,Roes K,et al. Dealing with missing outcome data in randomized trials and observational studies[J]. Am J Epidemiol,2012,175(3):210-7.

[10] Donders AR,van GJ,Stijnen T,et al. Review:a gentle introduction to imputation of missing values[J]. J Clin Epidemiol,2006,59(10):1087-91.

[11] MT Lozano Albalate,M Devy,J Miguel,et al. Addressing missing outcome data in meta-analysis[J]. Evid Based Mental Health,2014,17(3):85-9.

[12] Wood AM,White IR,Thompson SG. Are missing outcome data adequately handled? A review of published randomized controlled trials in major medical journals[J]. Clin Trials, 2004,1(4):368-76.

[13] White IR. Including all individuals is not enough : Lessons for intention-to-treat analysis[J]. Clin Trials,2012,9(4):396-407.

[14] Geert M,Herbert T,Ivy J,et al. Analyzing incomplete longitudinal clinical trial data[J]. Biostatistics,2004,5(3):445-64.

[15] Lane P. Handling drop-out in longitudinal clinical trials: A comparison of the LOCF and MMRM approaches[J]. Pharm Stat,2008,7(2):93-106.

[16] White IR,Higgins JPT. Meta-analysis with missing data[J]. Stata J,2009,9(1):57-69.

[17] Higgins JP,White IR,Wood AM. Imputation methods for missing outcome data in meta-analysis of clinical trial[J]. Clin Trials,2008,5 (3):225-39.

[18] Irving CB,Adams CE,Lawrie S. Haloperidol versus placebo for schizophrenia[J]. Cochrane Database Syst Rev,2013,11:CD003082.

[19] Tashkin DP,Kanner R,Bailey W,et al. Smoking cessation in patients with chronic obstructive pulmonary disease: a double-blind,placebocontrolled,randomized trial[J]. Lancet, 2001,357(9268):1571-5.

[20] Hajek P,Stead LF. Aversive smoking for smoking cessation[J]. Cochrane Database Syst Rev, 2004,3:CD000546.

[21] Sterne JA,White IR,Carlin JB,et al. Multiple imputation for missing data in epidemiological and clinical research: potential and pitfalls[J]. BMJ,2009,338:b2393.

[2 2]K L S a i n a n i. D e a l i n g w i t h n o n-n o r m a l d a t a[J]. PMR,2012,4(12):1001-5.

本文编辑：姚雪莉

Introduction of processing methods for missing data in Meta-analysis

YU Ya-yu*, XU Yang-peng, HE Qian, WU Jun-yi, FU Wen-jie, TAO Yuan, ZHANG Chao.*Center for Evidence-Based Medicine and Clinical Research, Taihe Hospital, Hubei University of Medicine, Shiyan 442000, China.

ZHANG Chao, E-mail: zhangchao0803@126.com

At the beginning of a clinical trial design, and even in the middle and later stages when data is tracked and followed up, partial data may be missed inevitably. However, when the missing data and research results are possibly linked, bias may be induced in a randomized controlled trial (RCT), and the bias risk will also be introduced to the results of Meta-analysis. Due to the status of missing data is very complex, processing methods for missing data should be selected according to actual situation. The aim of this paper is to present missing data mechanism including missing at random (MAR), missing completely at random (MCAR), missing not at random (MAR), and common processing methods.

Missing data; Available case analysis; Last observation carried forward; Imputed case analysis

R4

A

1674-4055(2016)12-1416-04

十堰市太和医院院级项目课题(2016JJXM070)

1442000 十堰,十堰市太和医院(湖北医药学院附属医院)循证医学中心;2442000 十堰,湖北医药学院口腔医学院12级;3442000 十堰,湖北医药学院影像医学院12级

张超,E-mail:zhangchao0803@126.com

共同第一作者：喻亚宇,许杨鹏

10.3969/j.issn.1674-4055.2016.12.03