门限秘密分享中高效添加新参与者方案
林修慧,林昌露,3,4,黄可可,李世唐
(1.福建师范大学 数学与统计学院,福建 福州 350117;2.福建师范大学 福建省网络安全与密码技术重点实验室,福建 福州 350007;3.桂林电子科技大学 广西可信软件重点实验室,广西 桂林 541004;4.重庆邮电大学 网络空间与信息安全重庆市重点实验室,重庆 400065)
Shamir[1]和Blakley[2]各自独立提出了秘密分享概念,并分别基于多项式和射影几何理论构造了具体的门限秘密分享方案。一般地,(t,n)门限秘密分享方案由分发阶段和重构阶段两部分组成,并有一个秘密分发者和n个参与者,其中t为门限值。在分发阶段,分发者把一个秘密随机地生成n个份额,并分别把这些份额通过安全信道秘密地发送给n个参与者;在重构阶段,只要大于等于t个参与者分别拿出自己的份额就可以正确地重构出秘密。1982年,Mignotte[3]提出了基于中国剩余定理(Chinese remainder theorem,CRT)的门限秘密分享方案。1983年,Asmuth和Bloom[4]改进了它的安全性,提出了安全的门限秘密分享方案。相较于Shamir的多项式门限秘密分享方案,基于CRT的秘密分享方案计算效率更高。
在门限秘密分享方案的实际应用场景中,有时需要增加新参与者。针对这样的场景,许多学者提出了可以添加新参与者的门限秘密分享方案。1988年,Ben-Or等[5]基于范德蒙德行列式,提出了可以添加参与者的门限秘密分享。2003年,Desmedt等[6]基于拉格朗日插值多项式,也提出了可以添加参与者的门限秘密分享。以上两个方案都是基于多项式的门限秘密分享,都不需要分发者的参与。在添加参与者过程中,需要原先的至少t个参与者的共同参与:参与者们两两互相发送一个值,每个参与者收到所有的值后再进行计算,之后把计算结果发送给新参与者,从而完成添加过程。在这过程中的总通信次数为t2次。
现有基于CRT的门限秘密分享文献[7-10]分别构造了添加参与者的方案。2016年,张明武等[7]提出了带权重的动态可验证门限秘密分享,可以验证秘密的有效性,但在添加参与者过程中需要分发者的参与,这使得这个方案无法在无可信分发者的具体场景中应用。2018年,王岩等[8]提出了动态门限签名方案,在添加新参与者过程不需要分发者,原先参与者仅需要互相通信一次,再与新参与者通信一次为新参与者生成新的份额,其总通信次数为t2次。2020年,洪璇等[9]提出了前向安全签名方案,但这个方案在添加参与者时需要可信分发者的参与,同样不适用于无可信分发者的具体场景。2020年,程亚歌等[10]提出了具有强前向安全性的动态门限签名方案,在添加新参与者阶段虽然不需要分发者的参与,其通信总次数也为t2次。上述添加新参与者的方案均是基于CRT的门限秘密分享,但是在添加新参与者阶段并不能做到无分发者且通信总次数均为t2次。
对此,本文基于Asmuth-Bloom门限秘密分享方案提出一个高效的添加参与者方案。在添加新参与者阶段,至少需要t个参与者参加;原先参与者之间不需要进行通讯,只需要通过安全信道向新参与者发送一个具体的数值。这个数值将由随机数掩盖,新参与者在收到所有的数值之后进行简单的模运算就能得到新的份额。
本文方案的优势如下:
(1)由于随机数的掩盖,保证了秘密和原参与者份额的信息不会泄露;在添加参与者过程中,不需要分发者的参与。
(2)在整个阶段的通信中,只需要有t个参与者发送一次值给新参与者,所以总通信次数为t次。
(3)在整个阶段中,因为原有的信息不会泄露,所以原来的份额不用改变,且分享的秘密值也不需要改变。
1 预备知识和安全模型
1.1 (t,n)门限秘密分享
(t,n)门限秘密分享方案[1]中t表示门限值,n表示参与者总数,设n个参与者为Pi(i=1,2,…,n)。一般地,(t,n)门限秘密分享方案由分发函数Share和重构函数Rec组成。
分发阶段:设S是秘密的取值集合。S由一个分发函数Share映射到S1×S2×…×Sn,Si是参与者Pi(i=1,2,…,n)对应份额的取值集合。分发者要分发一个秘密s∈S,计算Share(s)=(s1,…,sn),si∈Si,通过安全信道秘密地发送si给Pi。
重构阶段:至少有t个Pi拿出自己的份额si,然后执行重构函数Rec(si1,si2,…,sit)得到s。
(t,n)门限秘密分享需满足如下的正确性和安全性:
正确性:至少有t个参与者都拿出他们的份额后,可以正确的重构秘密,那么有H(s|{si1,si2,…,sit})=0。
安全性:就算任意小于等于t-1个参与者拿出他们的份额,他们也得不到关于秘密的任何信息,也就是有H(s|{si1,si2…,sit-1})=H(s)。
这里H(*)表示信息“*”的信息熵[11]。
1.2 中国剩余定理
中国剩余定理[12]是求解一次同余式组的方法,又称为中国余数定理或孙子定理。一次同余式组最早出现于中国南北朝时期的数学著作《孙子算经》中。下文是这个定理的详细介绍。
设m1,m2,…,mn为两两互素的正整数,即对任意的i≠j,i,j∈{1,2,…,n}时,有gcd(mi,mj)=1,这里gcd(a,b)表示为a与b的最大公约数。s1,s2,…,sn也为正整数,如果有如下的同余方程组成立
那么此方程组在模M下有唯一解,形式如下
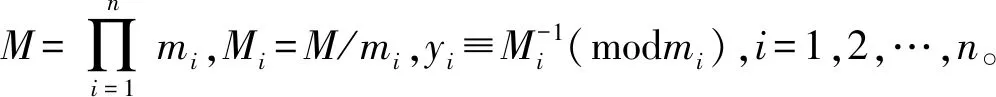
1.3 Asmuth-Bloom方案
Asmuth-Bloom方案[4]是基于中国剩余定理构造的(t,n)门限秘密分享方案,方案具体描述如下。
分发阶段:分发者公开选取一组满足下列条件的整数{p,m1,m2,…,mn}:
(1)mi (2)gcd(mi,mj)=1,i≠j,i,j=1,2,…,n; (3)gcd(p,mi)=1,i=1,2,…,n; 分发者秘密地选取秘密s,且0≤s 分发者计算si≡x(modmi),i=1,2,…,n,通过安全信道秘密地发送si给Pi。 重构阶段:每个参与者Pi公开自己的份额si,由中国剩余定理有 在一般的秘密分享中,通常考虑有两种类型敌手:外部敌手和内部敌手(也称为半诚实敌手),其中: (1)外部敌手没有合法的份额,但是会伪装成合法的参与者(持有份额的参与者)去参加秘密重构等,其目的就是获取秘密值或正确的份额; (2)内部敌手是合法参与者,会正确地执行协议,但是会试图获得其他参与者的份额。 本文所设计的方案在添加参与者阶段只考虑内部敌手,即秘密值是否会在添加参与者阶段泄露给参与者,合法参与者之间的份额是否会在添加参与者阶段互相泄露。 本文所构造的方案分为分发阶段,添加新参与者阶段,重构阶段3个部分。本文的主要贡献就是在添加新参与者这个阶段。添加参与者阶段:在无分发者的情况下,每个原先的参与者(大于等于t个)给新参与者不公开地发送一个由他们的私钥与随机数构成的数值;然后新参与者针对这些数值进行一些模计算,就能得到自己的份额。整个过程中秘密的信息不会暴露给任何人,每个参与者的份额也不会暴露给其他参与者(包括新参与者),在重构过程中新参与者也可以参加秘密的重构,并正确地重构出秘密。方案的具体过程如下。 添加新参与者阶段:任意t个原先持有份额的参与者随机选择一个随机数乘以mn+1,再选取一个随机数乘以M,然后与自己份额的计算结果相加之后将得到的值发送给新参与者。新参与者在收到至少t个参与者发送的值之后,进行一次求和运算与两次模运算就可以得到自己的份额。具体构造步骤如下。 (2)不失一般性,假设前t个参与者Pi,i=1,2,…,t。Pi随机选取一个随机数ri,0 那么sn+1就是新参与者Pn+1的份额。 重构阶段:这一阶段与1.3节所述的方案重构方法一致,这里不加赘述;唯一的不同就是n+1个参与者都可以参加重构。 针对方案的正确性分析,本文考虑的是新参与者从至少t个原参与者获取的份额应该和有分发者在的时候直接分发的份额是一样的,所以需要证明的是sn+1≡x(modmn+1)。 定理1如果在添加新参与者阶段步骤(1)、(2)中的参与者诚实正确地执行协议,那么Pn+1可正确地获得份额sn+1。 证明当Pn+1收到所有的ci(i=1,…,t)后,对它们进行求和模M运算,将会得到 对上式进行模mn+1运算有 所以,Pn+1可正确地计算出自己的份额sn+1,证毕。 本文主要考虑在分发过程中秘密不会泄露给任何参与者,任何参与者的份额不会暴露给其他参与者。由于t个参与者都是通过安全信道把信息传输给新参与者,所以只要考虑3个方面: (1)秘密是否会泄露给新参与者。 (2)原参与者的份额是否会暴露给新参与者。 (3)方案要满足t-1安全性。 由于在构造过程中每个用户子秘密都是由随机数掩盖,所以考虑新用户进行取模运算是否可能消掉随机数来获得子秘密或真实秘密的信息。 定理2对于内部敌手Pn+1,秘密值x不会暴露给Pn+1。 证明若Pn+1拿到ci,i=1,2,…,t后,直接对其进行模M计算,那么有 由于每个ri都是t个参与者随机选取,所以Pn+1不可能从上式的右边解出x,即Pn+1无法得知秘密的信息,证毕。 定理3对于内部敌手Pn+1,Pi(i=1,2,…,t)的份额不会暴露给Pn+1。 证明下面将对可能出现的3种情况进行分类讨论: 第二种:若Pn+1拿到Pi发过来的份额ci时,不进行求和,而对每个分开的ci单独进行如下计算 ci≡siMiyi+rimn+1+r′iM(modmi)≡ si+rimn+1(modmi) 由于ri是Pi随机选取的随机数,且gcd(mn+1,mi)=1,最后得到的结果依赖于ri的选取,所以Pn+1不能从上式的右边得到关于si的信息。 第三种:考虑Pn+1对ci进行模mn+1运算,得到 ci≡siMiyi+rimn+1+r′iM≡siMiyi+r′iM(modmn+1) 由于gcd(M,mn+1)=1且gcd(r′i,mn+1)=1,所以r′iM(modmn+1)的结果是未知的,故Pn+1不能从上式得到关于si的信息。 综上所述,Pi(i=1,2,…,t)的份额不会暴露给Pn+1,证毕。 定理4如果方案正确执行,那么任意的t-1个参与者得不到秘密的信息。 证明根据Asmuth-Bloom方案可知,在原先的n个参与者中,任意的t-1个参与者得不到秘密的信息,所以只需考虑Pn+1与另外的t-2个参与者共谋。在本文方案中,假设的是前t个参与者发送ci给Pn+1,所以要考虑两种情况: 第一种:发送ci给Pn+1的参与者{P1,P2,…,Pt-2}与Pn+1参与共谋。 第二种:没有发送ci给Pn+1的参与者{Pt+1,Pt+2,…,P2t-2}与Pn+1参与共谋。 在第一种情况中,{P1,P2,…,Pt-2}拥有{s1,s2,…,st-2},Pn+1拥有sn+1与ci=siMiyi+rimn+1+r′iM,i=1,2,…,t。这样,只需证明不能从{ct-1,ct}获得st-1或st的信息即可。因为rt-1,r′t-1是Pt-1独立选取的随机数,rt,r′t是Pt独立选取的随机数,所以ct-1和ct是独立的,根据定理3可知,不能从ct-1和ct中解出st-1或st的值,证毕。 在第二种情况中,{Pt+1,Pt+2,…,P2t-2}拥有{st+1,st+2,…,s2t-2},Pn+1拥有sn+1与ci=siMiyi+rimn+1+r′iM,i=1,2,…,t。这样,只需证明不能从ci中得到任意一个si即可。因为ri-1,r′i是Pi独立选取的随机数,所以ci是相互独立的,根据定理3可知,不能从单独的ci中解出任意的si。 综上所述,任意的t-1个参与者得不到秘密的信息,证毕。 本文所构造的方案在添加阶段不需要分发者的加入,通过增加随机数的方法保证了原先参与者的份额与秘密的信息不会泄露给新用户。在添加新参与者阶段没有额外的公开值,仅需t次通信总次数,新参与者在收到其他参与者发送的消息后,只需要进行简单的模计算就可以计算出自己的份额。总体而言,本文方案较大地降低了通信代价。表1是其他基于CRT的门限秘密分享方案[8-10]与本文方案在添加参与者阶段的详细比较。 表1 方案的特性对比 本文基于Asmuth-Bloom方案提出了一种基于CRT可实现添加参与者的门限秘密分享方案。在添加新参与者阶段,原先的每个参与者发送一个随机数掩盖的数值给新参与者,新参与者只需进行求模计算就能得到新的份额,从而完成分发过程。安全性分析表明本文方案保证了秘密的信息和原先参与者的份额信息不会泄露给新参与者。在不改变原方案任何信息的情况下实现了通信总次数为t的秘密分享方案。本文所提方案可以作为一种工具,比如嵌入到表1中其他方案或用于其他网络空间结构[14],以提高它们的通信效率,使它们具有更高的应用价值。

1.4 安全模型
2 本文方案
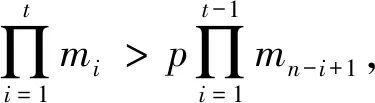
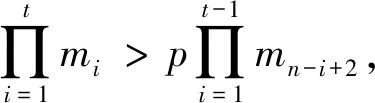
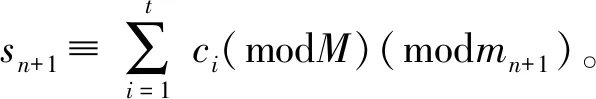
3 方案分析
3.1 正确性分析

3.2 安全性分析
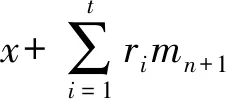
4 性能分析

5 结束语

