“和型”不等式的几种求解策略
“和型”不等式的几种求解策略
许雪芬李建潮
(浙江省湖州市双林中学,313012)
有关数列前n项和不等式的试题是当下高考的一大热点,今介绍几种常用的应对策略.
策略1待定系数法放缩通项
例1(2014年全国高考题)已知数列{an}满足a1=1,an+1=3an+1.
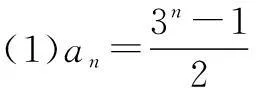
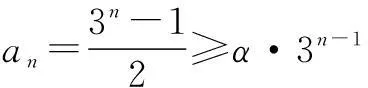

策略2待定系数法“裂”通项
裂通项求和是数列求和的一种行之有效的通法.这一策略可触类旁通地应用到“和型”不等式中来,如例1(2)的下列证法:
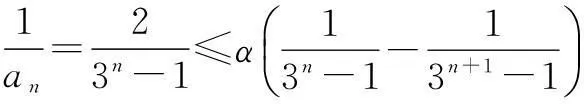
即α·3n≥3n+1-1,
(α-3)3n≥-1,n∈N*恒成立,
∴α-3≥0.
取α的最小值3,知对任意n∈N*,有
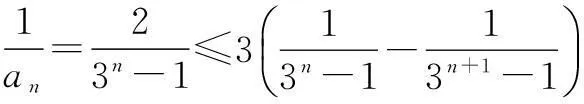
由此,立得

策略3改证“有(上)界”为“往后有(上)界”
例2(2004年全国高考题) 已知数列{an}的前项n和Sn满足Sn=2an+(-1)n.
(1)写出数列{an}的前3项a1,a2,a3;
(2)求数列{an}的通项公式;
(3)证明:对任意的整数m>4,均有
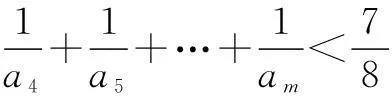
分析(1)略.
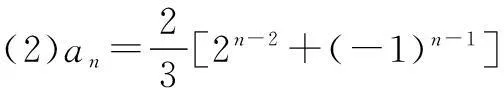
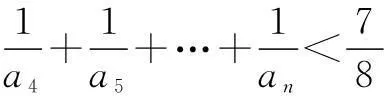
(*)
计算可得
这就是为什么本期写《童年的色彩》的小作者漆依芸说她的童年有那么多种色彩、写《玩具考古》的小作者吕兆恩有那么多“现代化”的玩具。小朋友们今天的幸福生活,跟小朋友们的爸爸妈妈小的时候相比,简直是有天壤之别,不信就看看本期的《童年的味道》和《远去的童年时光》吧。
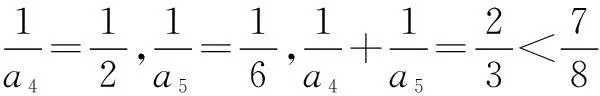
当n≥6时


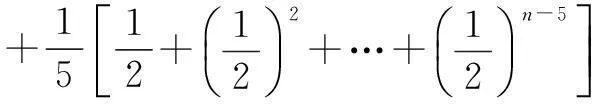

因此,当n≥6 时(*)式成立,即原不等式成立,得证.
评注以上第(3)小题也可以就m的奇偶性分类讨论证明,但明显繁琐.
策略4改证反向不等式


(*)
容易验证: 当n=1、2时(*)式成立.
当n≥3时,有
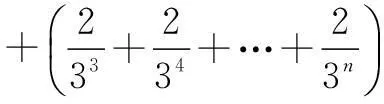
=(*)式的右边.
综上,对任意n∈N*,(*)式成立,原不等式获证.
策略5用增数列构造减数列
例4求证:

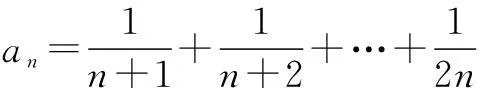
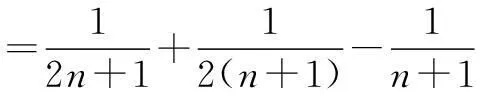
>0.
(*)
可见,{an}是增数列,但对正增数列求上界无济于事,为此设法通过(*)式构造出一个与之相关的减数列来.
事实上,由(*)式,可有



