聚焦非线性目标函数的最值问题
2016-03-02 11:51张世林,佘媛媛
高中数学教与学 2016年1期
聚焦非线性目标函数的最值问题
张世林佘媛媛
(湖北省巴东一中,444300)
在高考试题中,线性规划是高频考点,这类问题有两个难点:一是目标函数非线性;二是求线性规划问题中参数的取值范围.本文就第一类问题目标函数非线性,其最值的求法进行分类解析.
一、斜率型
例1已知实数x,y满足不等式
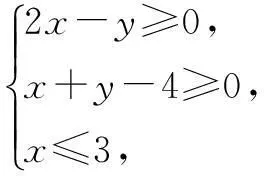

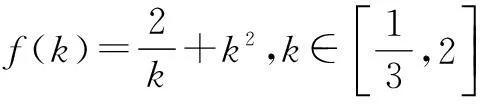
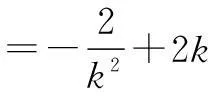
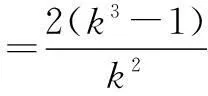
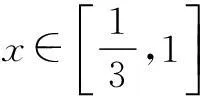

解条件5c-3a≤b≤4c-a,clnb≥a+clnc可化为

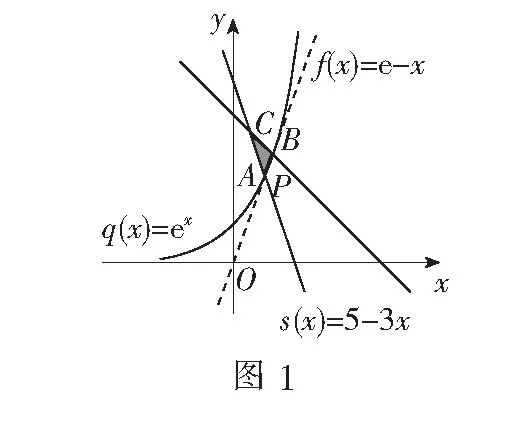
当(x,y)对应点C时,


二、距离型
1.点点距离型

(A)5(B)29(C)37(D)49
解作出不等式组表示的平面区域Ω(如图2阴影部分所示,含边界).圆C:(x-a)2+(y-b)2=1的圆心坐标为(a,b),半径为1,由圆C与x轴相切,得b=1.
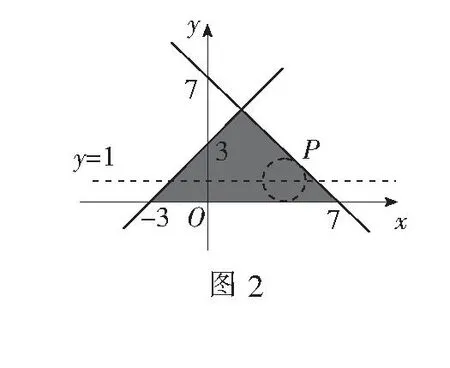
由条件,易得x=6,y=1,即直线x+y-7=0与直线y=1的交点坐标为(6,1),设此点为P.注意a2+b2表示点(a,b)到原点O距离的平方,又点C∈Ω,则当点C与P重合时,a取得最大值,所以,a2+b2的最大值为37,故选C.
2.点线距离型

三、数量积型(夹角型、投影型)
例5已知点P(x,y)的坐标满足
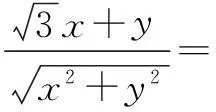




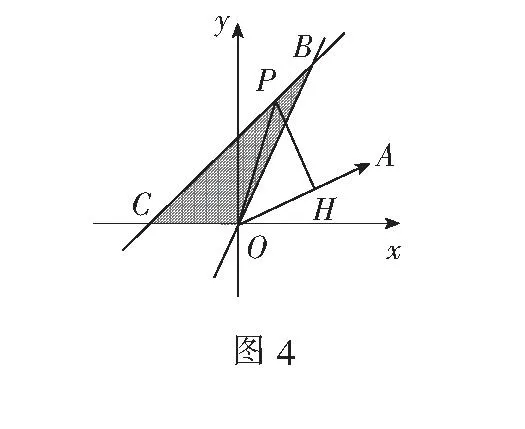
解(1)如图4,作出满足条件的可行域.根据平面向量数量积的几何意义,可得目标函数



四、直线与圆锥曲线相关位置型
例7设变量x,y满足约束条件
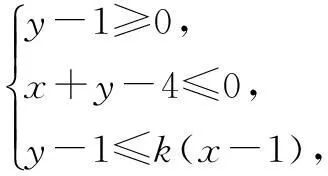
其中k∈R,k>0.
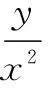
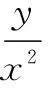
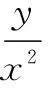


例8设x,y满足约束条件

若z=x2+4y2,则z的取值范围是______.

解根据约束条件画出可行域,z=x2+4y2表示中心在坐标原点,焦点在x轴上的椭圆,如图7.当此椭圆与直线x+y=1相切时,

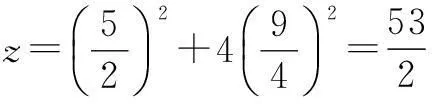
猜你喜欢
电机与控制应用(2022年4期)2022-06-27
中学生数理化(高中版.高二数学)(2022年3期)2022-04-26
中学生数理化(高中版.高考数学)(2021年12期)2021-03-08
河北理科教学研究(2020年3期)2021-01-04
中学生数理化(高中版.高二数学)(2020年11期)2020-12-15
现代苏州(2019年16期)2019-09-27
语言与文化论坛(2019年3期)2019-04-13
湖北文理学院学报(2017年2期)2017-04-16
燕山大学学报(2015年4期)2015-12-25
自然资源遥感(2014年2期)2014-02-27

