一道几何概型习题的错解分析
2016-03-02 11:51张开桃
高中数学教与学 2016年1期
一道几何概型习题的错解分析
张开桃
(江西省宜丰中学,336300)
求解几何概型的应用问题,关键是理解题意,准确构建几何概型.在构建几何概型的过程中,必须关注几何概型的两个基本特点:等可能性和无限性.本文结合教学过程中碰到的学生在一道几何概型习题中的几种错解,及该题的正确解法进行分析,希望能帮助大家在解题时完成对几何概型的构建.
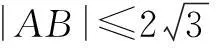
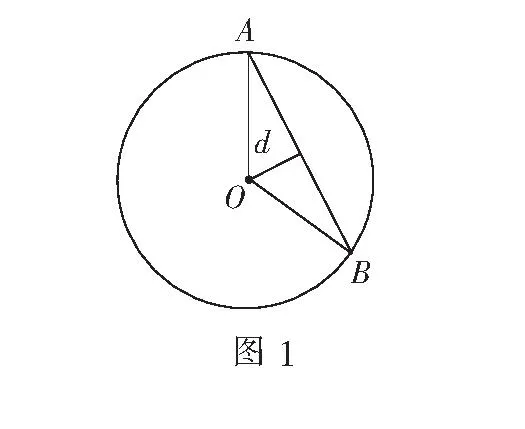

剖析根据几何概型概率的公式:P(A)=构成事件A的区域长度(面积或体积)÷试验的全部结果所构成的区域长度(面积或体积).
在求几何概型的概率时,既要找准事件A的区域长度,同时也要找准试验的全部结果所构成的区域的长度.本解法中弦|AB|所对的圆心角的范围应该是[0,π]而不是[0,2π],因此解答是错误的.

剖析根据几何概型的特点:任何一个点的选取都应该是等可能的,我们特别要注意“长度型”与“角度型”的不同,本题中,A、B两点是在圆弧上随机取点,是一个“角度型”的几何概型,把它转化为“长度型”,那么线段CD上的取点就不满足等可能性的特点,因此所求出来的概率是错误的.

剖析本题动点A、B是在圆上任意两点,它是与圆弧有关的几何概型,也即是与圆心角有关的几何概型.如果将它转化为与面积有关的几何概型,也不满足取点的等可能性,M点的圆内的取定不是等可能的,违反了几何概型的基本特点,因此,解答也是错误的.
下面提供三个正解.


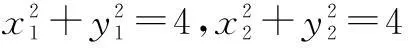
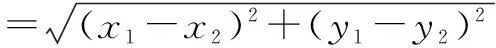
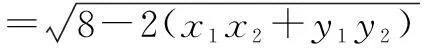
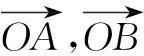
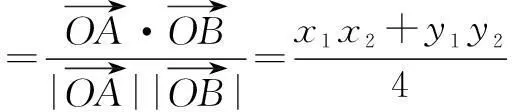
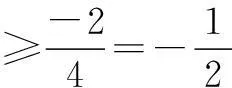

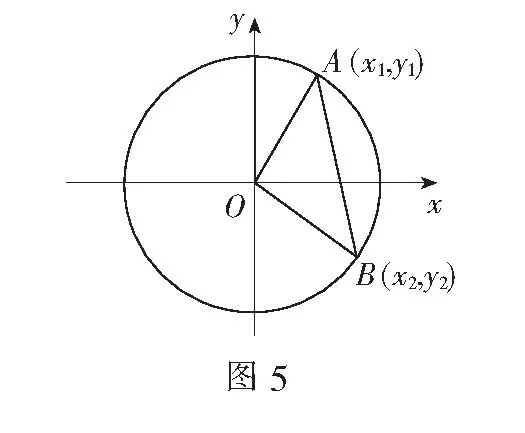
构建几何概型求概率,不仅要紧紧抓住几何概型的基本特点,而且要注意在应用几何概型概率计算公式计算时,测度是否一致.
○解题思路与方法○
猜你喜欢
科学与生活(2022年2期)2022-03-27
小学生学习指导(高年级)(2021年11期)2021-11-30
中学生数理化·高一版(2021年3期)2021-06-09
中学生数理化·七年级数学人教版(2020年11期)2020-12-14
中学生数理化(高中版.高考数学)(2020年10期)2020-12-04
中学生数理化·七年级数学人教版(2019年12期)2019-05-21
中学生数理化·高一版(2019年3期)2019-04-15
中学生数理化(高中版.高考数学)(2018年12期)2019-01-17
新世纪智能(数学备考)(2018年9期)2018-11-08
中学生数理化·高一版(2018年9期)2018-10-09

