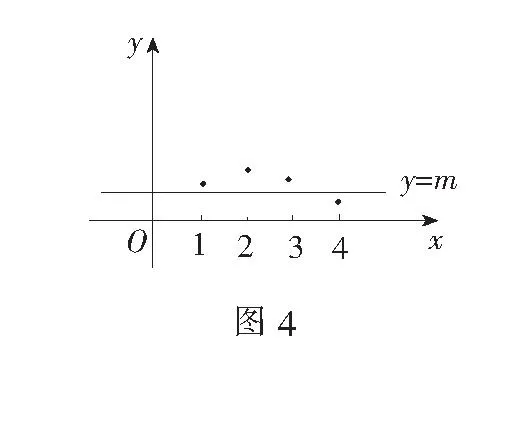
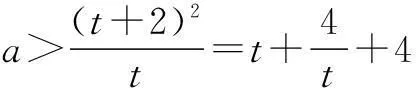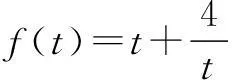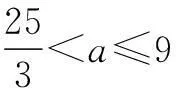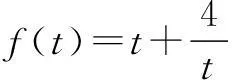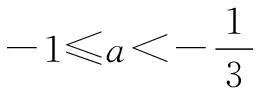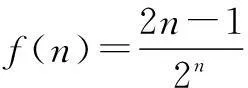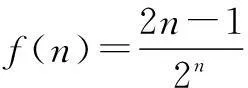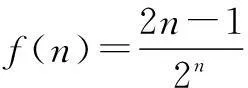不等式整数解问题的求解策略



不等式整数解问题的求解策略

徐广卫

(江苏省邗江中学，225009)

函数(数列)不等式是高中数学的重点内容,也是高中数学的难点,特别是含参数的不等式更是难上加难.这些不等式中有一类是关于不等式的整数解问题,学生常常感到难以入手.下面笔者试举几例来说明这类问题的常见求解策略．

一、直接求出不等式的解集,锁定解集中的具体整数解

例1若关于x的不等式ax2≥(3x-2)2解集中整数解恰有两个,求实数a的取值范围．

分析这是常见的一元二次不等式,可直接求出其解集,再根据该不等式对应的方程的根的特征锁定解集中的具体整数解．

解法1由题意，可知a>0，且

要使不等式解集中整数解恰有两个,必

二、利用函数的图象,锁定解集中的具体整数解

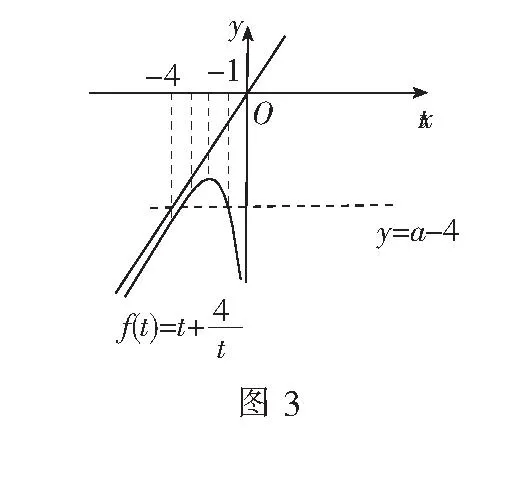
反思例1中由于含参数的不等式较抽象,学生难以入手,可考虑借助函数的图象获得如下直观求解．

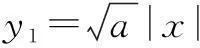
观察图象可得y1≥y2所对应的解集为[x1,x2],而x1∈(0,1),要使解集[x1,x2]中恰有两个整数,必需有x2∈[2,3)，即

评注这里是化归为一次绝对值函数图象求解．

例2若关于x的不等式x2-ax+2a<0的解集为A,且解集A中恰有两个整数,求实数a的取值范围．

分析这里，含参数的不等式难以锁定整数解的具体数值,可以考虑分离参数,利用函数的图象锁定解集中的具体整数解．

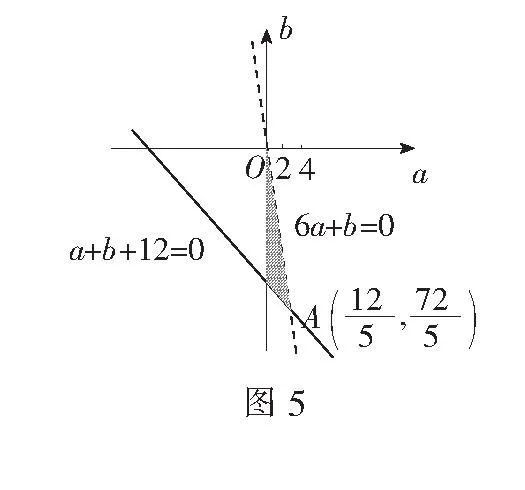
解∵x2-ax+2a<0,∴x2

令t=x-2,则t>0,又x∈Z,∴t∈N*，

令t=x-2,则t<0,又x∈Z,

∴t是负整数，

评注这里是化归为双钩函数图象求解．

例3若集合

中恰有3个元素,求实数m的取值范围．

又n∈N*,∴n≤1，

即f(1)f(3)>f(4)>f(5)….

评注数列不等式可化归为离散型函数图象求解．

三、利用函数不等式的几何意义,借助线性规划知识,锁定具体整数解

例4已知数列{an},{bn}都是递增数列,An(an,0),Bn(0,bn)(n∈N*),记直线AnBn的斜率为kn.若an=2n,bn=an+b(a,b∈Z),b1≥-12,数列{kn}前8项依次递减,求满足条件的数列{bn}的个数.

又数列{kn}前8项依次递减,

对(n=1,2,…,7)成立, 即an-a+b<0对n=1,2,…,7成立．

又数列{bn}是递增数列,∴a>0,故只要n=7,即7a-a+b=6a+b<0即可．

结合b1=a+b≥-12, 联立不等式

由线性规划知识作出上述不等式组所对应的可行域(如图5所示).

∴a=1或a=2.

即b=-13,-12,-11,-10,-9,-8,-7，有7解；

∴数列{bn}共有9个．

由以上几例的解法看出,处理函数(数列)不等式的整数解问题时,要把握问题的本质:一是这类问题自身就是不等式,故可从解不等式的角度，直接解出不等式的解集,再锁定解集中具体整数解;二是这类问题亦是函数,故可以通过化归、分离变量等渠道转化为利用函数的性质(单调性),挖掘代数式的几何意义,再结合函数的图象求解．