损失模型及其随机模拟

魏艳华（天水师范学院 数学与统计学院，甘肃 天水 741001）

损失模型及其随机模拟

魏艳华
（天水师范学院 数学与统计学院，甘肃 天水 741001）

研究保单限额、免赔额及通货膨胀率对理赔额的影响，利用随机模拟方法估计Pareto分布参数、分位数并对误差进行讨论.最后，在假定在损失额独立或同分布不成立的情形下，建立了总损失模型，并利用随机模拟探讨了总损额的性质，给出了模拟程序.

保单限额；损失模型；帕累托分布；时间价值；随机模拟

一张保单由于不确定性而发生的损失有多种结果，可以寻找一个合适的分布函数来刻画保单发生各种损失的概率，即损失分布.损失额是指承保的标的可能发生的实际损失大小，而理赔额是保险公司按保险合同规定的保单责任所支付的实际费用.对保险公司而言，理赔额是保险事故的实际损失额，保费、准备金、破产概率及再保险等精算问题都以保险人的实际赔付情况而定，因此，理赔额比损失额更值得关心.［1-4］保险公司为了规避风险及减少营业成本对保单责任进行限制.在总损失模型中，递推和逆变化法常要假设理赔额相互独立且和理赔次数相独立，这可能使模型不能反映现实情况.但是，在在损失额独立或同分布不成立的情形下，由于解析法得到的结果并不令人满意，因此关于总损失额的计算通常采用随机模拟的方法.［5-6］本文研究保单限额、免赔额及通货膨胀率对理赔额的影响，在责任险种，利用混合Pareto分布拟合损失数据非常成功，利用随机模拟方法估计Pareto分布参数、分位数并对误差进行讨论.最后在假定在损失额独立或同分布不成立的情形下，建立了总损失模型，并利用随机模拟探讨了总损额的性质，给出了模拟程序.

1　责任限制与通货膨胀对理赔额分布的影响

1.1保单限额

保单限额指每次保险事故中按保险单约定的最高赔偿金额，当损失金额超过保单限额时，投保人将只获得最高赔偿额，超出部分自己承担.［5］在财产保险中，保单限额就是投保额，为了规避道德风险，投保额最高不能超过财产的实际价值，即使投保人在几家公司同时投保，发生事故后，理赔总额也不会超过财产的实际价值，否则，投保人会任其发生事故，理赔后还会大赚一把，这违背了财险的补偿型原则，即赔偿数额不能超过财物的实际价值，避免保户通过理赔得到额外收益.但在责任保险，保单限额由双方协议.若保单规定保单限额为L，一旦发生事故，保险人必须赔付，即损失事件等于理赔事件.假定X为保险事故的实际损失，其分布函数为FX（x），Y为保险公司按保单规定保险责任的实际理赔额，则

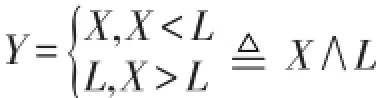
被保险人所获得的实际赔付额的期望值为EY，显然Y由一个离散分布和一个连续分布混合而成，密度函数与分布函数分别为

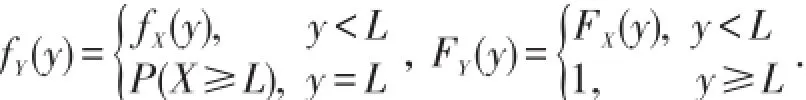
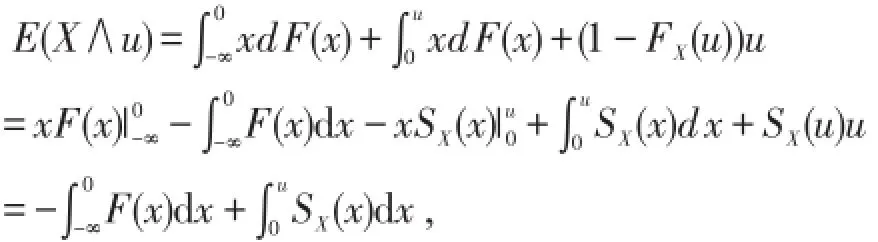
其中SX（x）=1-FX（x），称为生存函数.

特别有，若X是非负随机变量，则

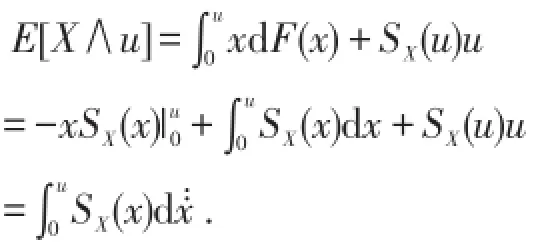
由全概率公式显然有

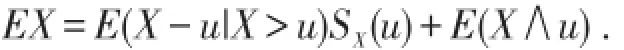
1.2免赔额

若保单规定，当损失额低于某一限额d时，保险公司不予赔偿，当损失额高于该限额时，保险人只赔偿高出部分.［6］这一限额称为普通免赔额，免赔额可以提高投保人的安全意识，主动防范风险，从而减少索赔次数，减少经营费用.试想，如果某此事故的损失额为200元，投保人申请理赔，则保险人就要派人去勘察、核实，这样会浪费很多人力、物力，特别会浪费双方当事人的时间，最后造成的社会总损失比200元可能还高，这也违背了保险的原则.若保单合同规定免赔额为d，则每次事故中被保险人实际获得的赔付

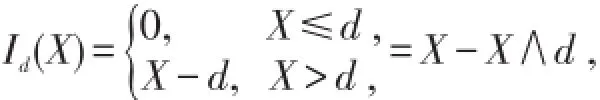
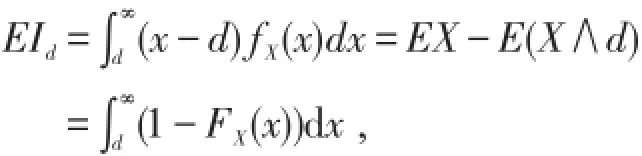
当损失额X≤d时，投保人不会提出索赔，保险人也无需理赔，因此理赔额也不存在.当损失额X＞d时，投保人才会提出索赔，赔付额为X-d.在每次损失事故中，保险人的理赔额

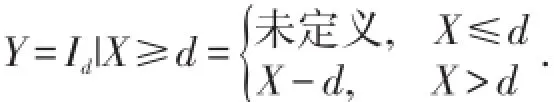
当y＞0时，

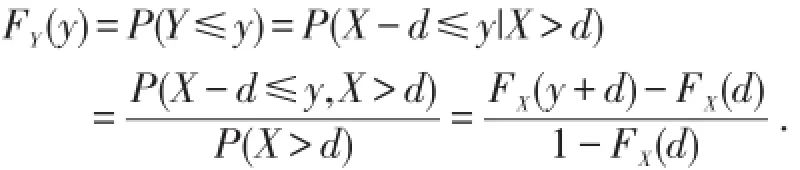
当y=0时，FY（y）=0.求导可得密度函数为

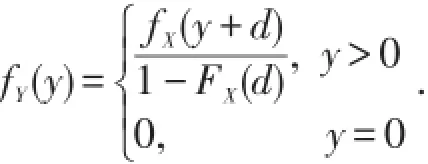
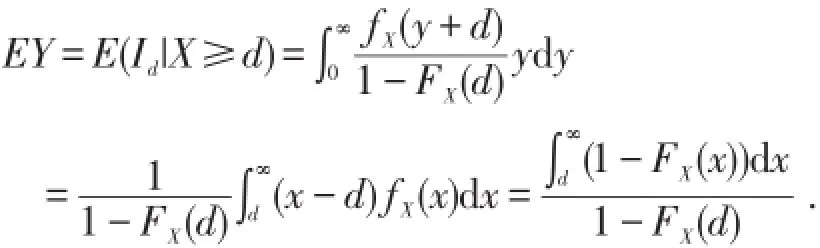
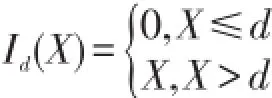
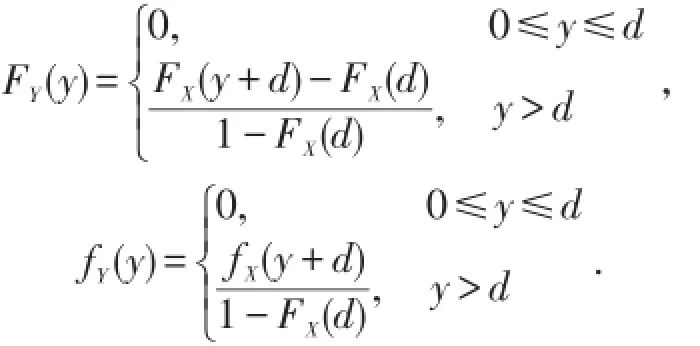
有些保单中规定，当保险事故实际损失额为X时，保险公司只赔付aX，这称为比例分担免赔，a称为比例分担系数.这时，理赔额Y=aX，

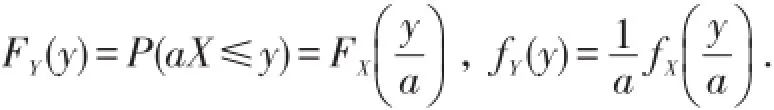
假定X为保险事故的实际损失，其分布函数为FX（x），Y为保险公司按保单规定保险责任的实际理赔额.若保单同时规定最高保单限额为L，免赔额为d，则每次事故的实际赔付为：

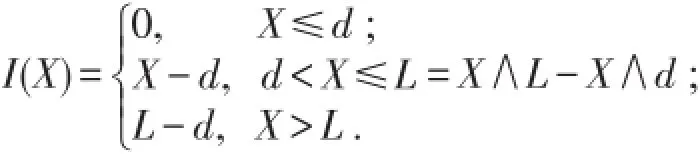
当0＜y＜L-d时，

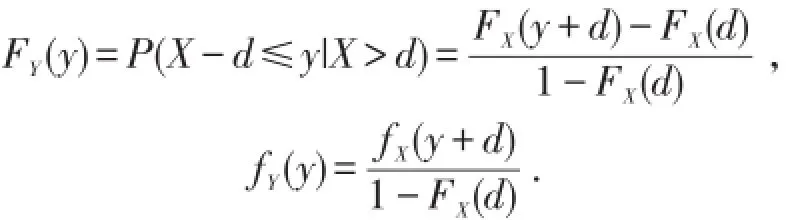
当y≥L-d时，FY（y）=1.

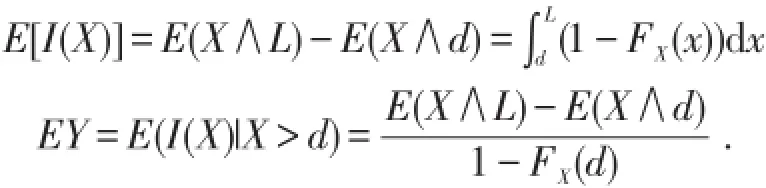
1.3通货膨胀

货币存在时间价值，即利率，同样由于国家为了增加财政收入，促进消费，增加就业，往往会采用征收通货膨胀税，即适度过量发行货币，这样，正常情况都会存在适度的通货膨胀.随着时间推移，损失额会随着通货膨胀而变大.

（1）当通货膨胀率为已知r时

设X为今年每次的实际损失额，预期通货膨胀率为r，则明年的实际损失Z=（1+r）X，分布函数为

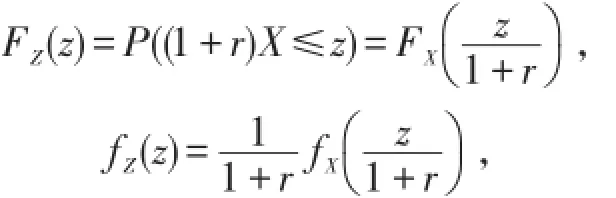
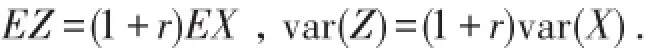
若X的分布函数 FX（x，θ）属于尺度（标度）不变分布，即FCX（x，θ）=FX（x，θ c），则通货膨胀后Z的分布函数形式没发生变化，只是参数发生了一定的变化.如指数分布族为一标准分布族，即尺度分布族，伽玛分布存在尺度参数.设随机变量X～Γ（α，β），对c＞0，令Y=cX，则

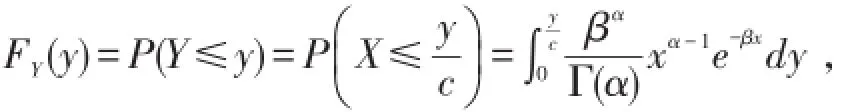
求导可得

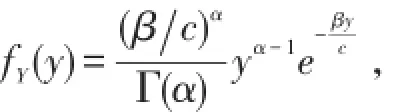
即Y～Γ（α，β c），因此伽玛分布的参数 β是尺度参数.

综上所述，设X为实际损失额，若保单规定免赔额为d，限额为u，比例分担系数为a，则每次损失事件的实际赔付额为I（X）和理赔额为Y，则E［I（X）］=a［E（X∧L）-E（X∧d）］，

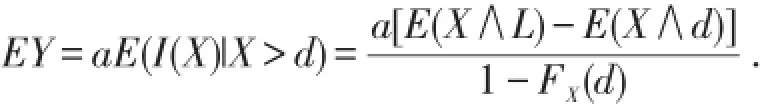
若预期通货膨胀率为r，且d，L，a在通货膨胀前后不变，则明年每次损失事件的实际赔付额为

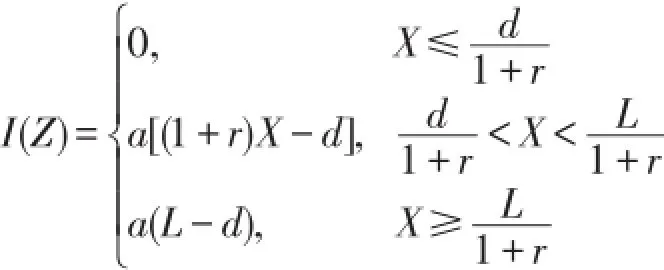
其中Z为理赔额，Z=I（Z）|X≥d（1+r），化简得

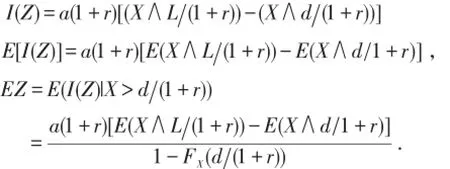
（2）当通货膨胀率是随机时

若年通货膨胀率为随机变量C，则明年的实际损失Z=CX，其中C与今年年实际损失额X相互独立，设C的分布函数为FC（c），密度函数为fC（c），则

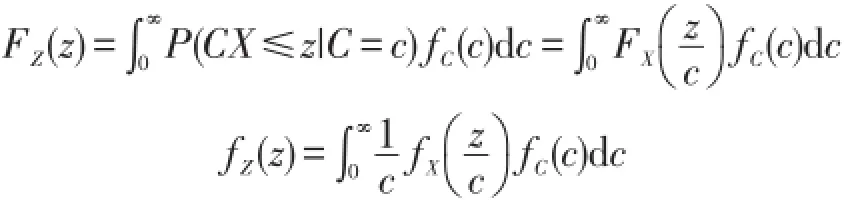
显然 EZ=E（CX）=E（C）E（X），由条件方差公式［4-6］

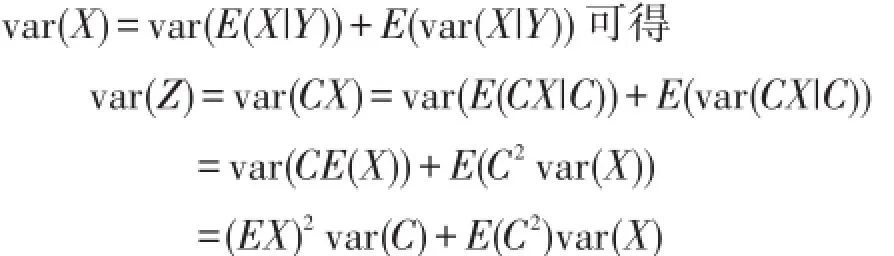
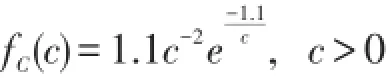
若明年的保单限额为30，求明年理赔额的期望.

解 设明年的损失额Z=CX，则

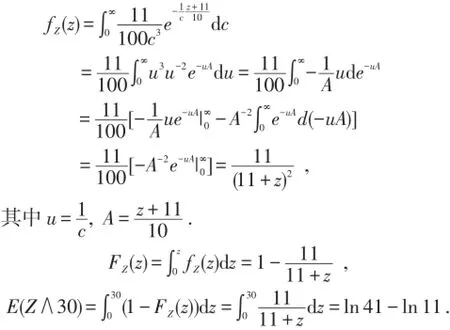
2　帕累托损失分布及其随机模拟

在损失模型中，只有选择一个合适的分布类型去估计损失额的分布，才可以较为精确地预测平均损失额或理赔额，进而才可考虑保费厘定、再保险安排等一系列精算问题.在非寿险中，很多损失数据具有厚尾特征，而Pareto分布具有厚尾，因此Pareto分布在数据模拟中具有广泛的用武之地.［7-8］意大利经济学家Pareto在研究收人数据时最先引进Pareto分布，目前，它广泛应用于极值分析，拟合保险损失，网络流建模，可靠性研究，以及金融风险管理等领域.

定义1［5］Pareto分布X的密度函数定义为

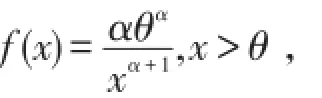
其中参数α＞0，θ＞0，分布函数为

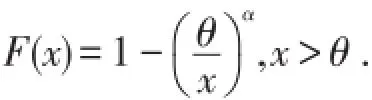
定义1是单参数Pareto分布，其实，只有α是真正的参数，θ的值必须预先确定.显然对于k＜α，

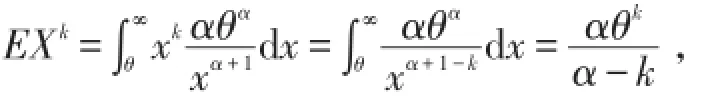
特别有

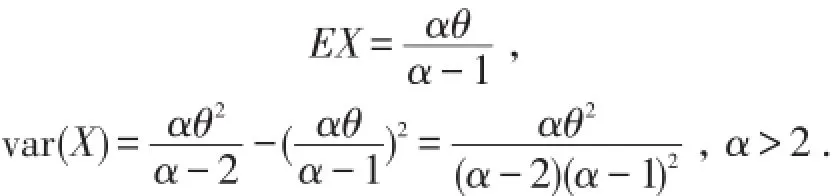
注意：当α＜2时，Pareto分布的方差不存在.众数恒为θ.

定义2［6］Pareto分布X的密度函数定义为

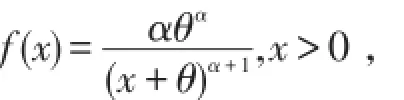
其中参数α＞0，θ＞0，分布函数为

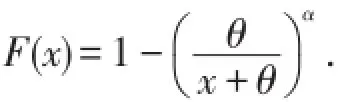
今后如不加声明，一般采用定义2.密度函数的右尾通常表示取值较大时的概率，精算师对这非常关注，因为高额索赔的发生对盈利的影响很大.如果随机变量X在取值较大的部分具有较高的概率，则称X具有厚尾.厚尾是一个相对的概念，如X比Y的尾厚，或是一个绝对的概念，如具有某种特征的分布称为厚尾分布.当选择模型时，考虑损失分布的尾部可帮助我们缩小选择的范围.如，对医疗事故索赔用Pareto分布模型是较为合理的，对牙医保险则应考虑对数正态分布较为合理，因为其尾部很轻.但是度量尾部轻重的方法并不一致.［6］如果任意整数阶矩存在，则说明尾部很轻，而整数阶矩存在最高阶或不存在，在说明尾部很厚.对于Γ（α，β）及∀k＞0，

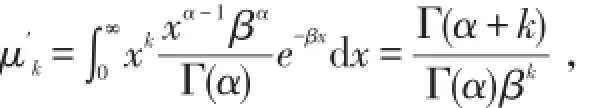
而对于Pareto（α，θ），

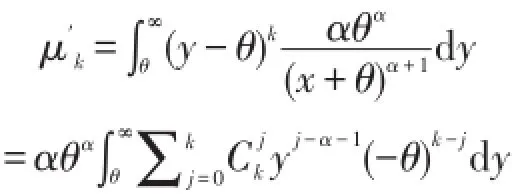
上述积分存在仅当和式中y的指数都小于1，即j-α-1＜-1对所有 j成立⇔k＜α.由于可见Pareto分布只有某些矩存在，故尾部比gamma分布厚.

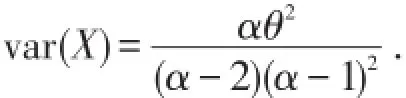
Pareto分布的尾比较厚，常用来描述损失分布，但保单存在限额x时，我们有：

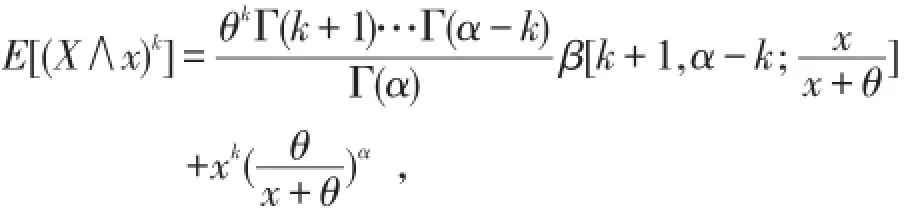
Pareto分布具有下述性质：

（1）Pareto分布总是右偏的，众数恒为0；

（2）Pareto分布乘以正常数r后，仍是Pareto分布，参数为（α，rθ）；

（3）如果均值EX=μ不变，当α→∞时，Pareto分布收敛到参数为1μ的指数分布.

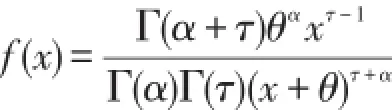
在广义Pareto分布中，令τ=1，可得到参数（α，θ）的帕累托分布.如果确定损失数据的尾部存在厚尾，我们一般可用广义帕累托分布来拟合损失数据，为了稳妥起见，应用条件的最大吸引域条件检验进行检验.在确定可使用广义Pareto分布来拟合存在厚尾的数据之后，一个重要的问题就是对损失数据进行分割，即找到一个科学且适当的门限值.只有找到了一个适当的门限值，对广义Pareto分布的参数估计才能得到一个成功的结果.

例2美国保险服务局的精算师发现，一般责任保险的损失模型采用2个参数的Pareto分布非常成功，并且不必要采用5个参数，他们选择的累积分布函数为

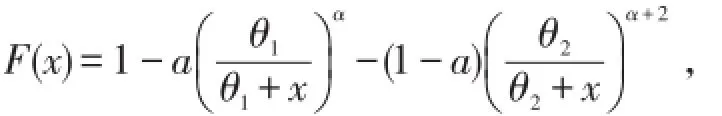
可见2个Pareto分布的形状参数相差2，第1个分布在取值很大的部分有较小的概率，它表示索赔额较大但不频繁发生的模型.第2个分布在取值很小的部分有较大的概率，它表示频繁发生且索赔额较小的模型.这个分布只有4个参数，一定程度上简化了建模工作.

一个简单的建模模型至少应具有以下特点：

（1）当可以使用较少的参数确定模型时，确定每个参数的精度应很高；

（2）模型要对时间和环境稳定.如发生通货膨胀或类似想象引起的一些微小变化，模型仍然可以用；

（3）由于数据通常是不规则的，所以简单的模型应便于进行必要的光滑处理；

当然使用较多参数确定的复杂模型可以与现实吻合的更好，可以更准确地匹配数据的不规则性.［5-6］统计建模所遵循的过度节约原则是：应选择能够充分反映现实情况的最简单的模型，就像购买商品，要买你买得起的最好商品，对充分的理解应依赖于模型的用途.

目前获得Pareto随机样本仍很困难，但我们可以做出一些让步，利用Pareto伪随机数来代替帕累托随机样本，因为不知二者来源的人不能将二者区分开，这样的一个伪随机序列完全可以满足我们的需求.如果F（x）是分布函数，u～U［0，1］，则

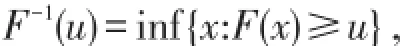
是一个F随机数.由

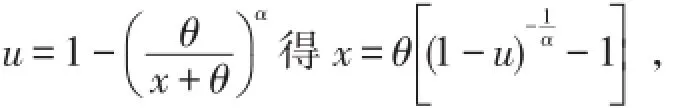
为参数为Pareto（α，θ）随机数.［7］

例3生成10000个伪Pareto（3，1000）随机数并验证无法将其与真实的Pareto分布观察值区分开.利用随机模拟估计均值、FX（1000）以及90%分位数π0.9，当n多大时，你确信有95%的概率得到的模拟结果与与真实值的误差为±1%？

解 由商业化软件生成均匀随机数u，由公式x=1000［（1-u）-1 3-1］可得到Pareto伪随机数.程序省略，模拟结果如下表：

表1　特征数

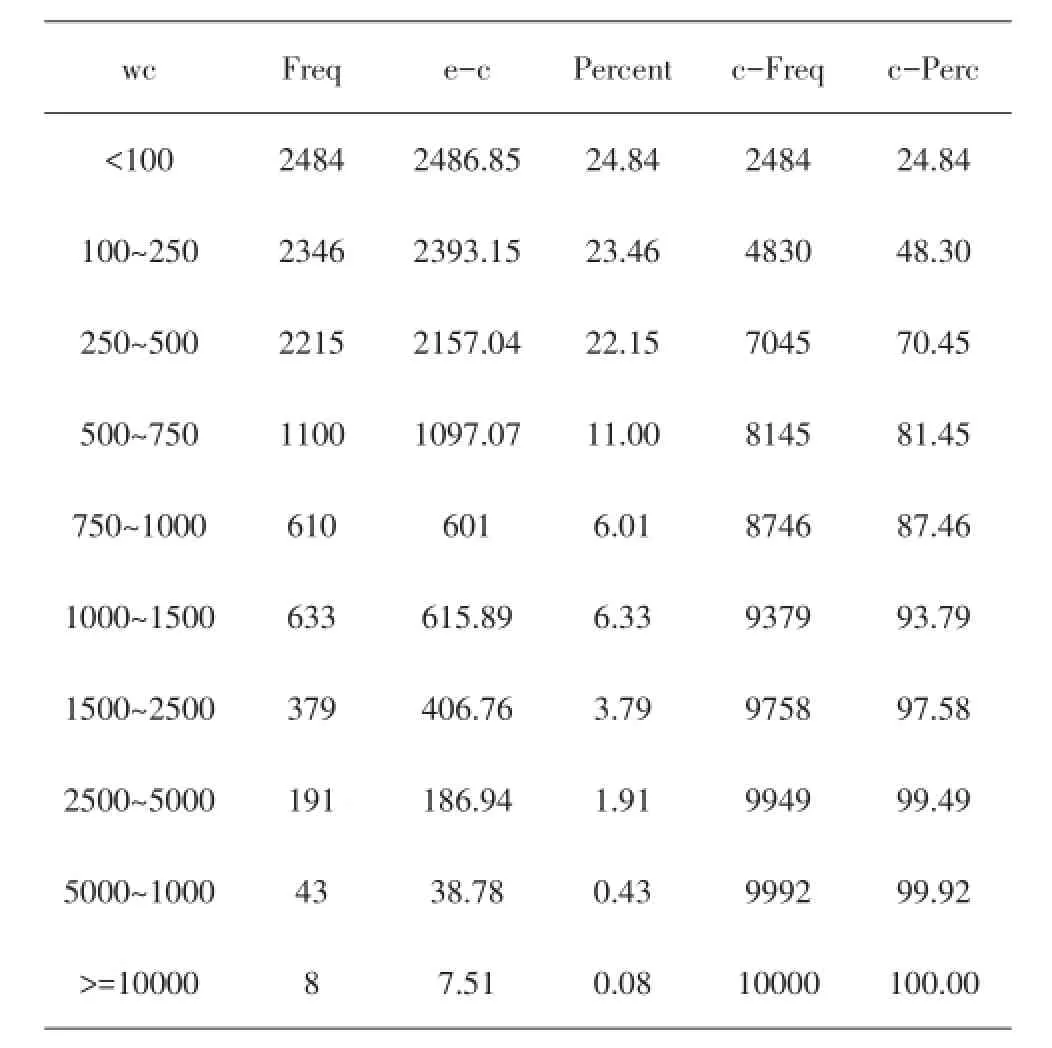
表2　频数表

由于均值、标准差分别为

模拟的结果为

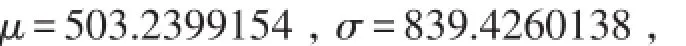
可见结果还是挺好的.由于

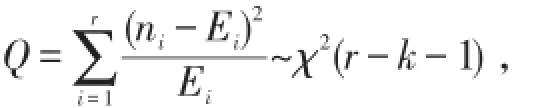
ni，Ei是第i个区间实际出现的次数和理论出现次数，k为未知参数的个数，如果计算得到的统计值，则拒绝原假设.程序运行结果为，Q=5.578927426＜14.067，接受原假设，即无法将无伪帕累托随机数与真实的Pareto分布观察值区分开.由于均值μ的经验估计为x¯，由中心极限定理，

在样本容量为n时，有

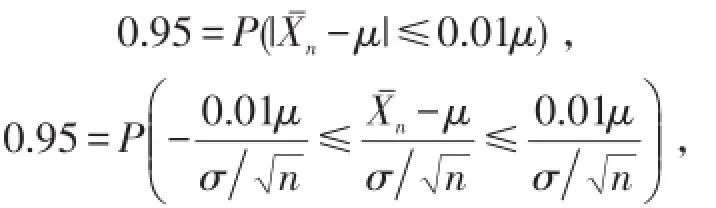
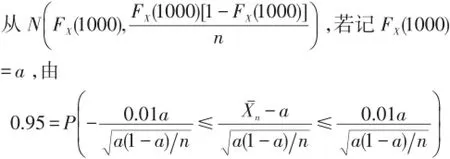
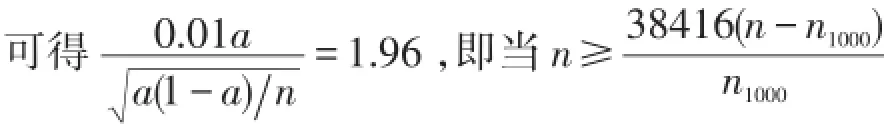
成立时可满足要求.

当n=10000次时，n1000=8746，

完全可以满足要求，这时的估计值为0.8746，真实值为0.8750，相对误差为0.0457%.

假如 X（1）≤X（2）≤…≤X（n）是模拟样本的次序统计量，令

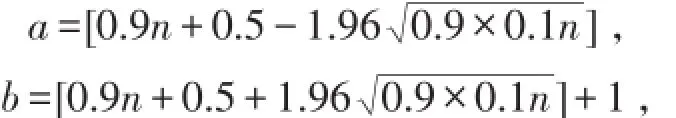
则0.95=P（X（a）≤π0.9≤X（b））.

可见模拟10000次，即使没有满足停止规则，可模拟误差达到了要求.可见停止规则只是给我们提供了一种参考的方式，由于数字的随机性及利用样本均值和样本方差代替均值和方差的近似性，导致了结果具有不小的误差.

3　总损失模型

独立性或同分布在以下两种情形下常不成立，一是考虑时间，如货币的时间价值，二是承保责任的调整.［6］

（1）损失赔付的时间价值

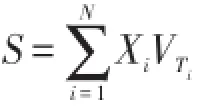
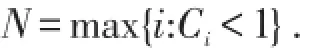
（2）含投保人最大自留额的情形

假设对每一笔损失都考虑免赔额d，但是在一年中，投保人自己的支付不会超过u.用Xi表示第i笔损失，Wi=Xi∧d表示免赔额为d时投保人的支出，Yi=Xi-Wi表示保险人的支付，则R=W1+…+WN表示没有支付上限时投保人的总支付额，显然投保人的实际支出为 Ru=R∧u.S=X1+…+XN表示一年内的总损失额，则保险人的总支付T=S-Ru.当S和Ru的分布都基于独立同分布索赔额的分布时，我们可利用解析法求得他们的分布，但是因为存在相依性，不能通过合并的方式得出T的分布，也不存在一种方法将T表示成i.i.dYi的和.虽然在年初时，看起来T表示成独立同分布的Yi的和，但是在某些点投保人的总支付额达到上界u 时Yi将被Xi取代.

假定免赔额d=250，赔付上界u=1000，损失次数N～NB（3，2），损失额服从参数τ=2，θ=600的威布尔分布，分布函数为试给出保险人损失为95%的分位数.

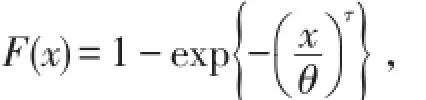
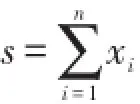
（3）随机模拟

只给出情形（1）的随机模拟，（2）同理可得.假设Xi～Pareto（3，1000），Li服从参数τ=1.5，θ=ln（Xi）6的威布尔分布，分布函数为，可见尺度参数依赖于损失量.对于贴现因子，我们假定当t＞s，

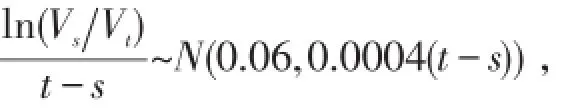
由于由损失时间间隔可推出损失次数N，故不必对N假设.下面通过随机模拟法计算一年总赔付期望的贴现值.

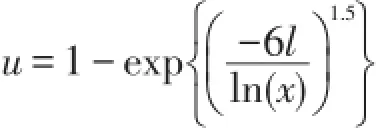
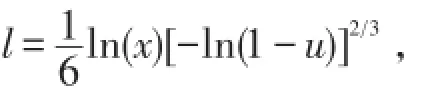
其中x为损失量.损失的最终支付时间ti是ci合li之和.

最后生成贴现因子，先将ti按升序排列，又因为

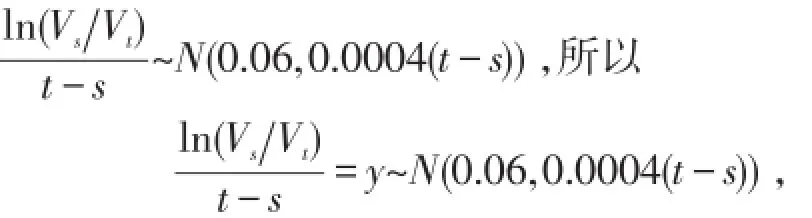
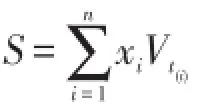
由于每年的索赔次数随机性太强，可能1次，也可能4此或7次，这样就导致结果的随机性很强，表现在模拟的方差很大，达到了106级，但我们的模拟结果还具有一定的参考价值，一年总赔付贴现值为2300左右.

特别值得注意的是：如果再进行同样程序运行，模拟次数仍为100次，结果可能不一样，普遍在2300左右.由于每年的索赔次数随机性太强，导致，总赔付限制的方差可能随次数的增加而增加.

由于均值μ的经验估计为x¯，由中心极限定理，在样本容量为n时，有

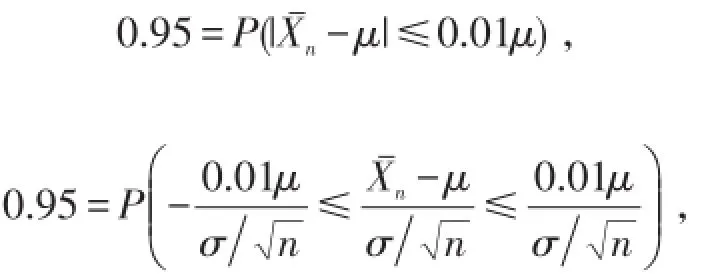
［1］孙树旺，江涛.具扩散项的带免赔额的Erlang（2）问题的破产概率［J］.中国管理科学，2007，15（5）：35-40.

［2］王丙参，魏艳华.伽玛分布的优良特性及其在风险管理中的应用［J］.宁夏师范学院学报，2010，31（6）：21-24.

［3］何树红，李如兵，董志伟.常利率下理赔额受限的风险过程［J］.云南大学学报（自然科学版），2005，27（5A）：640-614.

［4］魏艳华，王丙参，徐长伟.停止损失保费的计算与近似［J］.天水师范学院学报，2010，30（5）：18-20.

［5］肖争艳.风险理论［M］.北京：中国人民大学出版社，2008：15 -50.

［6］KLUGMAN S A，PANJER H H.损失模型从数据到决策［M］.吴岚，译.北京：人民邮电出版社，2009，（1）：30-520.

［7］刘曼莉，李兴绪.非寿险精算中的数据尾部拟合与保费厘定［J］.统计与决策，2011，（4）：14-18.

［8］赵智红，李兴绪.非寿险中巨额损失数据的拟合与精算［J］.数理统计与管理，2010，29（2）：336-347.

〔责任编辑 高忠社〕

Losses Model and its Stochastic Simulation

Wei Yanhua，Wang Bingcan，Zhang Yixin
（School of Mathematics and Statistics，Tianshui Normal University，Tianshui Gansu741001，China）

The paper discusses that policy limits，deductibles and inflation impact on the claim amount distribution.By using stochastic simulation method estimates parameters and quantiles of Pareto distribution，discusses the error of simulation.Last it establishes the total losses model when losses are not independent and identically distributed，discusses the property of total losses by using stochastic simulation method，gives the simulation program.

insurance policy limits；losses model；pareto distribution；time value；stochastic simulation

O211.9

A

1671-1351（2016）02-0009-07

2016-01-21

魏艳华（1978-），女，吉林四平人，天水师范学院数学与统计学院讲师。