联合生存概率准则下最优变损再保险研究

王淑敏 房 莹

( 山东师范大学数学与统计学院，250358，济南 )

1 引 言

从二十世纪六十年代开始，最优再保险的研究已经经历了半个多世纪的历史，最优再保险也成为近年来越来越流行的课题之一.在精算文献中，关于最优再保险研究的文献已有许多，例如Centeno(1991)[1]，Sung(2011)[2]，Chi和Weng(2013)[3]，Kaluszka(2005)[4]，Promislow和Young(2005)[5]以及Cai和Tan(2007)[6]等人的文献.这些文献的一个共同特征是最优性考虑的是一方的利益，即保险人的利益.通过采取再保险策略，保险人能控制他们的全部风险.出于不同的目的，保险人可以通过不同的方式来设计再保险策略.例如Sung等人(2011)通过最大化保险人财富的期望效用函数来研究最优再保险策略，而Chi和Weng(2013)则是通过最小化保险人的风险损失(VaR)来研究最优再保险策略.从风险管理的角度来看，最小化保险人损失的风险价值(VaR)是一种流行的再保险模式，例如Kaluszka (2005),Promislow和Young(2005)以及Cai和Tan(2007)等人的文献中都采取了这种模式.

一份再保险合同涉及保险人和再保险人两方，并且双方有利益冲突.因此，如果我们只考虑保险人的利益，对于再保险人来说可能并不公平.Borch(1969)[7]指出对于保险人的最优再保险合同对于再保险人来说可能不是最优的，也可能是不可接受的.关于最优再保险，一个有趣的问题是设计一种再保险，使其兼顾保险人和再保险人两方的利益.Borch(1960)[8]首先考虑了这个问题，他研究了使双方财富的期望效用函数的乘积最大化的最优比例保留额和最优止损自留额.Cai等人(2013)[9]研究了比例再保险和止损再保险在期望值保费原则下，保险人和再保险人的联合生存概率函数以及联合盈利概率函数的最大化问题.

本文是在Cai等人(2013)最优准则的基础上，研究了最优的变损再保险策略.通过研究他们的联合生存概率函数，给出了最优变损再保险策略存在的充分必要条件，并且得到了最优的自留额与比率.

2 变损再保险

假设X是保险人总的风险损失，我们假定X是一个非负随机变量，并且有分布函数F(x)=Pr{X≤x}，生存函数S(x)=1-F(x)以及均值EX=μ>0.

变损再保险是一种简单的分保形式，是指当损失X0的情况.

因再保险人分担保险人的部分风险，故保险人应以保费的形式向再保险人支付费用.我们假设保险人和再保险人的保费按照期望值原则计算，那么再保险人和保险人的保费收入分别为

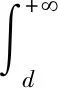
(1)

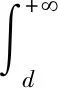
(2)

其中θI,θR分别为保险人和再保险人的安全负荷因子，uI>0,uR>0分别为保险人和再保险人的初始财富.

在实务中，保险人会将风险更大的损失转移给再保险人，不失一般性，我们假定θI<θR，另外，从收益角度来看，保险人获得的保费收入PI(c,d)必须是正的，因此有

(3)

3 保险人和再保险人的联合生存概率

在变损再保险中,比率c与自留额d组成参数组合(c,d),设D为可行的比率与自留额区域，故有

在变损再保险中，保险人和再保险人的联合生存概率函数为

Js(c,d)=Pr{XR≤uR+PR(c,d),XI≤uI+PI(c,d)}

(4)

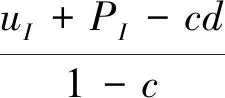
定理1在D区域内，以下集合均是非空的：

(5)

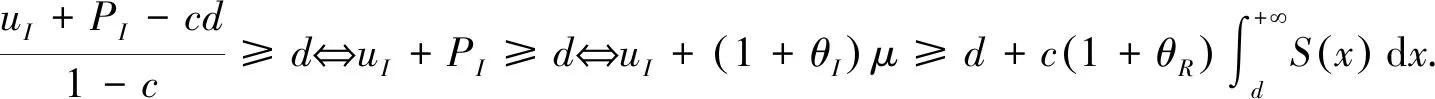
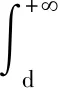
又因为G1(c,d)关于c,d是连续的，所以集合(5)均是非空的.定理即证.

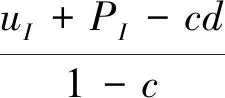
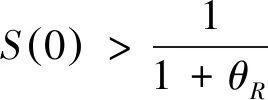
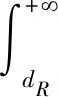
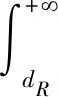
(6)

证

(7)

(8)

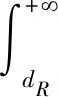
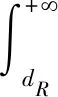
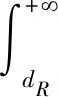
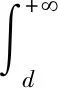
又因为(1,dR)∈D,所以，当c→1,d→dR时，由(7)和(8)得

(9)

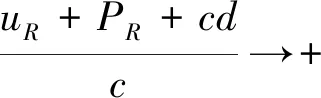
(10)

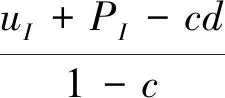
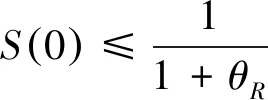
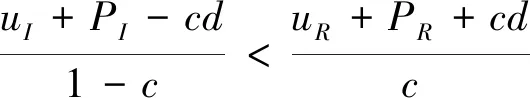
(ii) 如果uI>(θR-θI)μ,那么以下集合均是非空的：

(11)

证明同定理2，故在此省略.

最后，我们得出保险人和再保险人的联合生存概率函数.

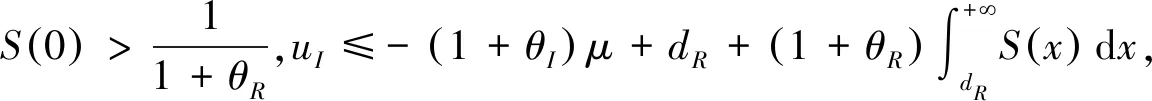
(12)

(13)

其中

(14)

4 最优再保险参数

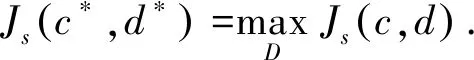
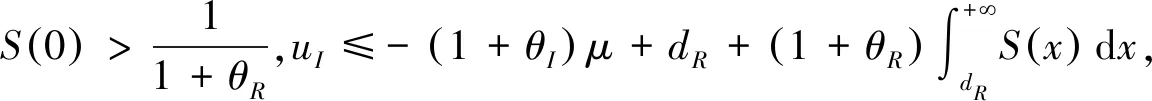
证由定理4(i)知保险人和再保险人的联合生存概率函数为(12)，如果d≤uI+PI,那么

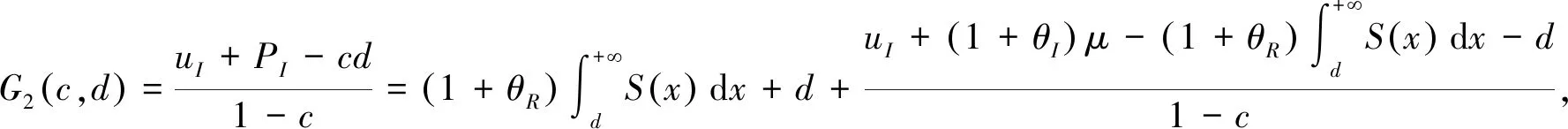
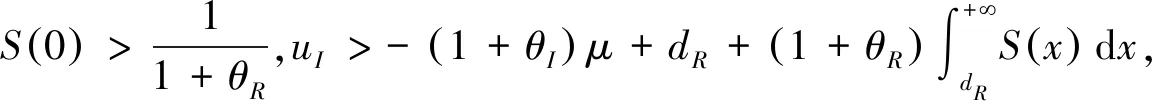
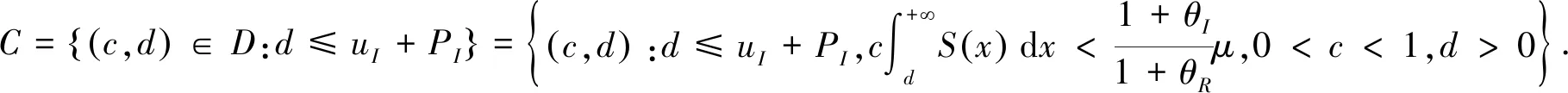
证由定理4(ii)知保险人和再保险人的联合生存概率函数为(13)，当d≤uI+PI时，

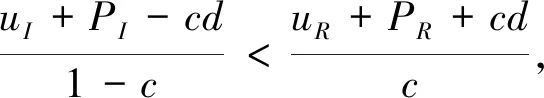
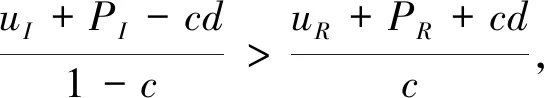
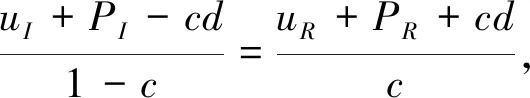
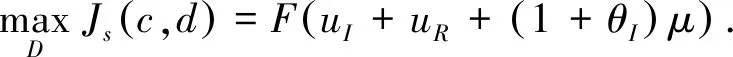
例1令θI=0.2,θR=0.4,uR=50,uI=20,假设X有指数型分布的生存函数S(x)=e-0.01x,μ=100,

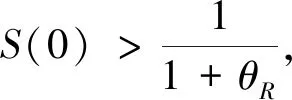
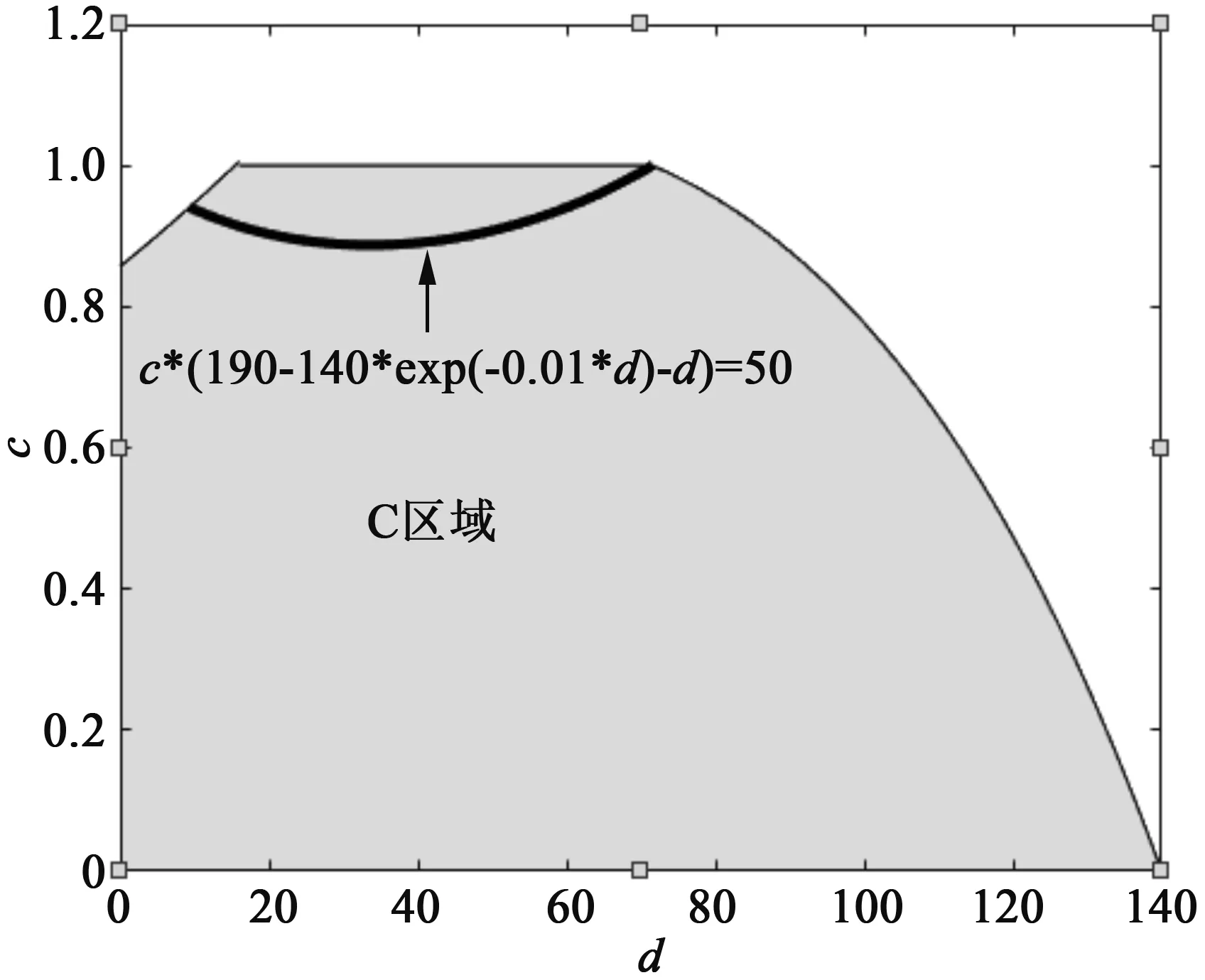
图1 例1的最优参数组合

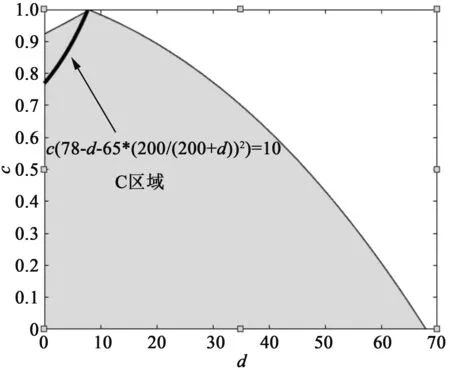
图2 例2的最优参数组合

例2令θI=0.2,θR=0.3,uR=10,uI=8,X有帕累托型分布的生存函数

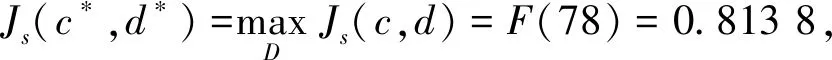
5 结 语

在本文中，我们研究了联合生存概率准则下变损再保险的最优策略.首先，给出了在变损再保险下保险人和再保险人的联合生存概率；其次，在期望值保费原则下，最大化双方的联合生存概率函数，得到了变损再保险最优的自留额与比例；最后，给出了变损再保险最优自留额与比例的数值分析.我们还指出了需要做进一步研究的问题.首先，多重最优条件的存在通常成立，因此，需要第二个标准来选择唯一的最优再保险参数(c,d)；其次变损再保险可以推广到其他形式的再保险.对于这两个问题，我们希望在未来能做更进一步地研究.