基于效用最大化理论关于保险人监管成本的分析

吕会茹， 王永茂， 管 巍， 王 红

(燕山大学理学院 河北秦皇岛066004)

0 引言

提到保险欺诈，人们往往会联想到投保人或被保险人的保险欺诈行为.然而，近年来保险公司的欺诈行为也屡见不鲜［1］.其最主要的原因是保险市场中的信息不对称.在保险交易中，可以依据保险合同双方将信息不对称分为两类:一类是因为保险标的通常被投保人与被保险人所控制，而保险人不容易了解保险标的风险状况的信息不对称;另一类是由于投保人以及被保险人不了解保险人的偿付能力的信息不对称［2］.本文主要在第2种情况下进行分析.

绝大部分保险人自身财富水平和承担风险能力有限，会通过购买再保险分散风险［3-4］，因此再保险人为了自身的利益会对保险人的监管水平进行监督，避免因保险人道德水平不高，给自身带来经济损失.本文提到的道德水平有两层含义:一是保险人的偿付能力是否充足;二是保险人在承保期间，对投保人的监管水平.

1 模型的假设条件

本文中，假设只有一位保险人和再保险人，且投保人为同质的，仅要求赔付一次保险金.其他具体假设条件为:

1)假设保险人为风险厌恶者，财富水平s，且s＞0，也可视为偿付水平为s，效用函数的形式为u(s)=-γe-γs，γ ＞0，则有u'(s)=γ2e-γs＞0，u″(x)=-γ3e-γs＜0，绝对风险厌恶系数为 γ［5］．令再保险人是风险中性的，且其期望利润为零．

2)假设保险人对投保人进行监管的成本为c，且c≥0．因为保险人对投保人的监管水平决定着其赔付率，所以可以假设保险人对投保人的赔付率为p(c)．一般来说，监管成本越多，则监管水平越高，赔付事件发生的概率越小，即p'(c)＜0，p″(c)＞0．若赔付事件发生，赔付额为定值α，赔付率为p(c)，那么赔付事件未发生(赔付额为零)的概率为h=p(0)=1-p(c)．同时，令

应注意到这里的参数λ＞γ．

3)若保险人进行再保险，则令保险人交付给再保险人的保费为π．当赔付事件发生时，保险人赔付给投保人的保险金为α，从再保险人处得到的保险金额为β(β≤α)．且假设保费的形式为π=p(c)·β，可知再保险的保费π是保险人监管成本c和再保险金β的函数，亦可记为π=π(c，β)．

定义1 设使保险人对投保人赔付最小，期望效用最大的最优监管成本为c*，称c*为有效监管成本，其表达式为 c*=(ln(λhα))/λ．

2 保险人偿付能力不足时保险人的监管水平

当保险人的偿付能力不足时，由于受到自身财富水平的限制，不能承担投保人损失发生时应赔付的保险金额，此时有s＜α．有时虽然保险人进行了再保险，但因受到签订合同中再保险金的限制，也不能完全赔付投保人的保险金．一旦投保人发生损失且要求赔偿，保险人只能赔付s．

当保险人的偿付水平s=α时，因为保险人是厌恶风险的，所以只要其进行再保险一定能提高自身的效用水平;当保险人的偿付水平s≤c+p(c)·α时，进行再保险会使自身效用水平降低，故存在某一偿付水平s0(c+p(c)·α＜s0＜α)为是否进行再保险的临界点，使(2)式成立，

p(c)·u(-c)+［1-p(c)］·u(s0-c)=p(c)·u(s0-α-c-π+β)+［1-p(c)］·u(s0-c-π)．(2)

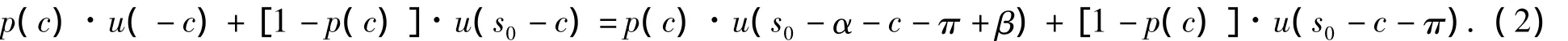
2．1 不进行再保险时的监管成本

从自身效用出发，保险人不进行再保险需要满足的条件是

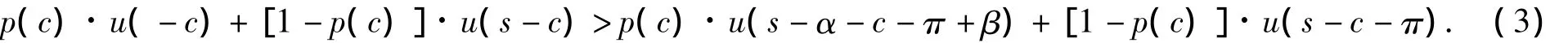
当保险人偿付能力不足时，无法对投保人进行足额的赔付，投保人不能得到的保险金额为α-s．由此可得，保险人能够赔付的保险金的期望为p(c)s，投保人自行承担的赔偿为p(c)·(α-s)．此种情形下，保险人为了自身效用的最大化，需要做的是选择合适的监管水平，即

定理1 当保险人偿付能力不足且不进行再保险时，存在临界财富水平s*使其选择是否对投保人进行监管，且时，则保险人不会对投保人进行监管，即 c=0;当s∈(s*，α)时，则保险人会对投保人进行监管，且监管成本，可知保险人财富足够少时，其会选择不监管，即c=0;保险人的财富很少时，期望赔付的保险金也很少，想通过提高监管程度来降低赔付的保险金幅度也很小，为了自身效用最大化，其会不进行监管，即c=0．因此，可以认为有一临界财富水平s*使其选择是否监管．可以通过模型(6)求得

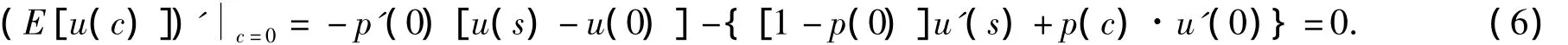
证明 对式(4)两边求c的一阶导数，可得

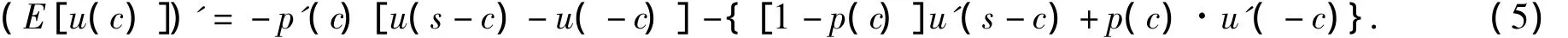
从上式的结果可知，当保险人的偿付能力不足时，如果其对投保人进行一定的监管，那么监管水平与不监管时的赔付概率h以及自身偿付水平s成正相关．并且赔付概率h越大，对投保人赔付的期望降低幅度就越大，保险人就会愿意进行高水平的监管工作;保险人的偿付水平越高，其承担的赔付责任比重越大，其所逃脱的责任越少，这种情况下提高监管水平就会大幅地减少自己的赔付金额．因此，保险人是很愿意进行高水平的监管的．

2．2 进行再保险时的监管成本

若保险人进行了再保险，再保险人就会在投保人发生损失且要求赔偿时，承担部分赔偿责任，这样就会

若s∈(s*，α)时，则偿付水平为s的保险人会对投保人进行一定的监管，即监管成本c＞0．此时可求出使保险人效用最大化的监管成本满足一阶最优条件，由式(7)有

把式(1)和保险人的效用函数u(s)=-γe-γs代入式(8)，可得c

把式(1)和保险人的效用函数u(s)=-γe-γs代入式(6)，从而临界财富水平(即临界偿付水平)s*为有效地解决保险人因财富水平有限导致的偿还能力不足的问题．若其进行再保险，为使自身效用最大化需满足(9)式，

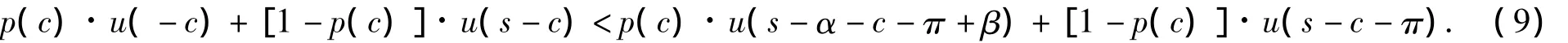
从2．1节的分析可知，不等式(9)与s0＜s＜α等价．当投保人不要求赔付时，保险人的财富水平为s-π;当投保人要求保险人理赔时，保险人的财富水平变为s-π-α+β．那么，保险人此种情况下的期望效用模型为 E［u(c)］=p(c)·u(s-α-c-π +β)+［1-p(c)］·u(s-c-π)．

与保险人对投保人的行为进行监管一样，再保险人也会对保险人的行为进行监督．假设存在一个随机变量θ，表示再保险人能够监督到的保险人对投保人监管水平，因为变量θ与再保险人实施监督的时间有关，所以再保险人监督到的保险人的监管水平与保险人真实情况的监管水平是存在差异的，即为θ-c．

定义2 设θ=c+ε，其中ε为随机扰动项，其分布依赖于c．若ε=0，则称再保险人对保险人是完全监督的，即再保险人的监督水平与保险人的监管水平无差异;若ε特别大，则称再保险人对保险人是完全不能监督的，即再保险人的监督水平与保险人的监管水平无关．

定理2 当保险人偿付水平不足且满足条件s∈(s0，α)和θ=c时，则有 β=α，c=(ln(λhα))/λ．证明 当θ=c时，有π=π(c，β)=p(c)·β．保险人为使自身效用最大化，满足的数学模型为

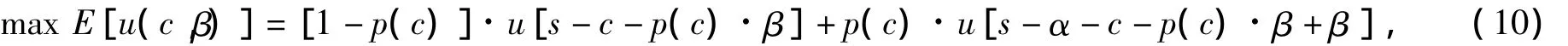
对式(10)两端分别求c和β的一阶偏导数且令偏导数为0，有

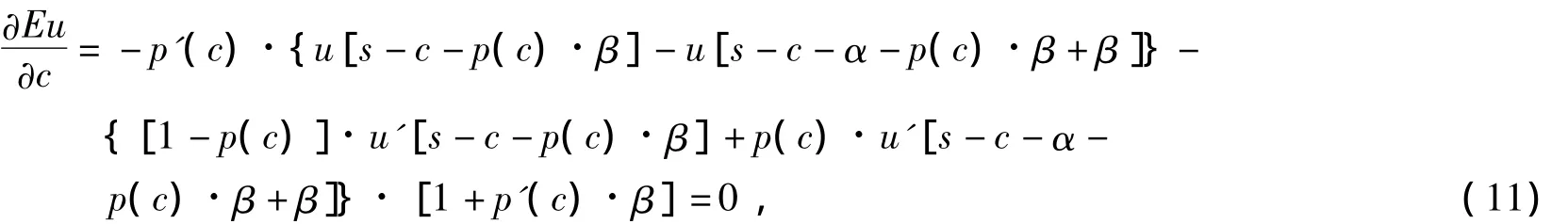
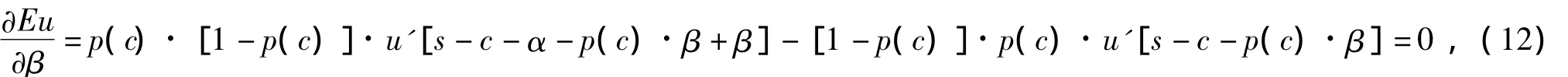
把式(1)和保险人的效用函数代入式(11)和式(12)，可得β=α，c=(ln(λhα))/λ．

由此可知，若再保险人能完全监督到保险人的监管水平，那么保险人会转移全部的风险，投全额的再保险，同时对投保人进行有效地监督．

定理3 当保险人偿付水平不足且满足条件s∈(s0，α)及θ与c无关时，则有

证明 当θ与c无关时，有π=π(β)=p(c)·β．即在再保险人完全不能监督时，保险人支付的再保险费仅与再保险合同上规定的再保险金β有关．保险人为使自身效用最大化，满足的模型为

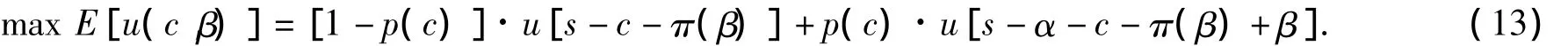
同理，对式(13)两端分别求c和β的一阶偏导数且令偏导数为0，有

把式(1)和保险人的效用函数代入式(14)和式(15)，解方程组可得

由此可知，若再保险人完全不能监督到保险人的监管水平，那么保险人仅会进行部分的再保险．

3 保险人偿付能力充足时保险人的监管水平

第2节分析了保险人偿付能力不足时存在道德风险，这是一种保险人的欺诈方式．然而，当保险人偿付能力充足时，由于其道德水平低下，为了自身利益，也会有欺诈行为发生．

3．1 不进行再保险时的监管成本

利用效用理论可知，保险人不进行再保险时应满足条件是

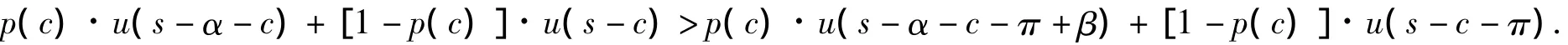
因保险人是风险厌恶者，且再保险的保费为π=p(c)·β，不满足(5)式．可知，保险人一定会进行再保险来提升其自身的效用．因此，本文不再对此种情形进行讨论．

3．2 进行再保险时的监管成本

众所周知，保险人进行再保险的目的是为了通过再保险来提高自己的效用，用效用函数描述为

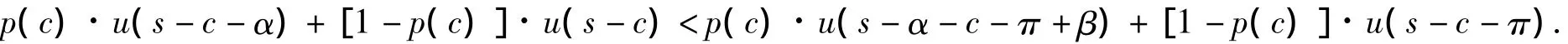
当投保人不要求赔付时，保险人的财富水平为s-π;当投保人要求保险人理赔时，保险人的财富水平变为s-π-α+β．那么，保险人此种情况下的期望效用模型为

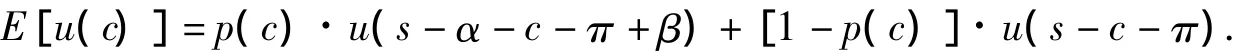
与2．2节对比可知，保险人偿付水平充足时进行再保险的期望效用模型与其偿付水平不足时进行再保险的期望效用模型是一样的．因此，本文不再对此种情形进行分析．

4 建议

从上面的分析中可以得知，当保险人偿付能力不足时，若进行再保险且再保险人对其监督水平越高，越可以促进保险人的监管水平.这说明再保险人对保险人的行为有着约束作用.但是，保险人不进行再保险时，这种约束就不起作用了.因此，也需要保监会和社会大众对其进行监督.

信息不对称是保险行业中出现欺诈的主要原因，而且保险人偿付能力不足是保险欺诈的主要形式之一，就此我国需加强立法，要求保险人增加信息透明度，定期向社会公众发布自己的财政信息.同时，对于违反保险法的公司，要加大处罚力度，对于表现好的保险公司可给予一些奖励，例如可以通过减少税收的方式.

［1］ 唐芳.保险公司也欺诈［J］.经营与管理，2006，22(5):20-21.

［2］ 陶存文.中国保险交易制度成本研究［M］.上海:立信会计出版社，2005.

［3］ Sonderman D.Reinsurance in arbitrage-free markets［J］.Insurance:Mathematics and Economics，1999，10(2):191-202.

［4］ Kaluszka M.Optimal reinsurance under mean-variance premium principles［J］.Insurance:Mathematics and Economics，2001，28(1):61-67.

［5］ 吴岚，王燕.风险理论［M］.北京:中国财政经济出版社，2006.