具有不耐烦顾客的M/M/1单重工作休假排队系统

徐 刚, 于泳波

(1.东北石油大学 秦皇岛分校 基础部 河北 秦皇岛 066004；2.秦皇岛兴荣海事中等职业学校 基础部 河北 秦皇岛 066100)

具有不耐烦顾客的M/M/1单重工作休假排队系统

徐 刚1, 于泳波2

(1.东北石油大学 秦皇岛分校 基础部 河北 秦皇岛 066004；2.秦皇岛兴荣海事中等职业学校 基础部 河北 秦皇岛 066100)

讨论了一个具有不耐烦顾客的M/M/1单重工作休假排队系统.工作休假期到达的顾客变得不耐烦并激活一个服从负指数分布的计时器，如果在计时器到期之前顾客没能完成服务，则该顾客离开系统，永不返回.通过平衡方程和母函数推导出正规忙期和工作休假期的平均队长等性能指标的解析表达式.通过数值算例考察了两个服务率对系统性能指标的影响.

不耐烦顾客； 工作休假； 排队； 平衡方程； 母函数

0 引言

在过去的20年里，休假排队模型得到了广泛深入的研究，其研究成果已应用到很多领域[1-3].近几年，工作休假排队和具有不耐烦顾客的排队成为研究的热点.文[4-9]引入工作休假并研究了不同工作休假的排队问题，采用多种方法得到排队模型并对数值结果进行了分析.

本文在经典M/M/1单重休假排队系统中增加了顾客的不耐烦性和休假期并未完全停止工作两个新的影响因素，利用平衡方程和母函数，推导出忙期和工作休假期的平均队长等性能指标的解析表达式.通过数值算例考察了两个服务率对系统性能指标的影响.

1 模型描述

考虑一个具有不耐烦顾客的M/M/1单重工作休假排队系统，系统中只有一个服务台，每次只能接待一位顾客，并假设：

1) 顾客按照参数为λ的Poisson流到达.

2)每位顾客所需的服务时间服从负指数分布，在忙期服务员的服务率为μb.现加入单重工作休假规则：一旦系统中没有顾客即正规忙期结束，服务员立即进入一个随机长度为V的工作休假中，休假时间V服从参数为θ的负指数分布.与通常的休假策略不同，服务员在假期内并未完全停止工作，而是以较低的速率μv(≤μb)为顾客服务.当一次工作休假结束时，如果系统中已有顾客在等待，服务员立即停止工作休假，服务率由μv提高到μb，一个正规忙期开始；否则，服务员进入闲期，直到有顾客到达，正规忙期才开始.

3)在工作休假期顾客变得不耐烦.即假期内到达的顾客排队等待时间T后仍未完成服务则离开系统，永不返回.假设顾客在进入系统直到离开的这段等待时间T服从参数为ξ的负指数分布.

4)假设到达过程、服务过程以及休假过程相互独立，服务规则为先到先服务(FCFS).

2 稳态分析

下面将对所描述的模型进行稳态下的分析，首先给出服务员处于工作休假期和非工作休假期(正规忙期或闲期)的顾客数的母函数，然后推导忙期和工作休假期的平均队长的表达式，最后还可得到平均等待队长、平均离去率等性能指标.

2.1平衡方程和母函数

令L(t)表示时刻t系统中的顾客数，即系统的队长，t≥0.令J(t)表示时刻t服务员的工作状态，

则{J(t),L(t),t≥0}为二维马尔科夫过程，其状态空间为Ω={(0,n):n≥0}∪{(1,n):n≥0}.

系统中稳态概率定义为：

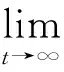
平衡方程定义为：

(θ+λ)p00=μbp11+(μv+ξ)p01,n=0，

(1)

(λ+θ+μv+nξ)p0n=λp0,n-1+(μv+(n+1)ξ)p0,n+1,n≥1，

(2)

λp10=θp00,n=0，

(3)

(λ+μb)p1,n=θp0,n+λp1,n-1+μbp1,n+1,n≥1.

(4)

2.2平均队长

下面利用平衡方程和母函数求解忙期平均队长E[L1]和假期平均队长E[L0].

将(3)，(4)对所有n相加得

θp0·=μbp11,

(5)

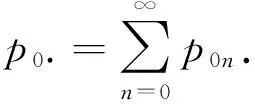
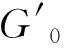
(6)

将(4)两边同乘以zn，然后加(3)并整理得

G1(z)((λz-μb)(1-z))=θzG0(z)-(μbp11-μbp10)z-μbp10.

(7)

(6)可改写为

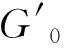
(8)

(8)两边同乘以exp(-λz/ξ)(1-z)θ/2ξz(μv+θ/2)/ξ,整理得

对两边求0到z的积分得

ξexp(-λz/ξ)(1-z)θ/ξzμv/ξG0(z)=μvp00k1(z)-μbp11k2(z)，

(9)

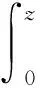
令z→1有

μbP11k2(1)=μvP00k1(1).

(10)

(7)式可改写为

G1(z)=(θzG0(z)-(μbp11-μbp10)z-μbp10)/(λz-μb)(1-z).

(11)

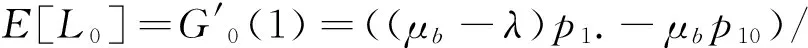
(12)

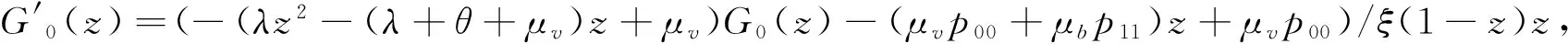
(13)

由(13)解得

E[L0]=((λ-μv)p0·+μvp00)/(θ+ξ).

(14)

而且由(11)可得

(15)

由正规化条件及(3)，(5),(10),(12)，(14)解得:

p0·=(θ+ξ)(μb-λ)/θ(λ-μv+kθ+(θ+ξ)((μb-λ)/θ+μbk/μvλ)),

p00=(θ+ξ)(μb-λ)k/μv(λ-μv+kθ+(θ+ξ)((μb-λ)/θ+μbk/μvλ)),

p10=θ(θ+ξ)(μb-λ)k/λμv(λ-μv+kθ+(θ+ξ)((μb-λ)/θ+μbk/μvλ)),

其中k=k2(1)/k1(1).

2.3其他性能指标

(a)系统的平均队长E[L]=E[L0]+E[L1].

(e)服务员处在闲期的概率PI=p10.

只要λlt;μb,系统就能处于平稳状态[9].在本模型中，当μv=0即为文献[9]所讨论的一个模型,且结果一致，从而验证了本文的正确性.

3 数值算例

首先利用matlab软件计算出两个定积分k1(1)和k2(1)的值，然后利用第2节的有关公式给出系统性能指标的数值结果，并考察忙期服务率和工作休假期的服务率对系统性能指标的影响.

表1和表2分别给出了忙期服务率μb和工作休假期的服务率μv在不同的数值下系统性能指标的数值计算结果.在表1中，取参数λ=4,ξ=1,θ=2,μv=5.在表2中，取参数λ=4,ξ=1,θ=2,μb=7.

表1 μb取不同值时系统的各项性能指标Tab.1 Performance measures of the system with different μb values

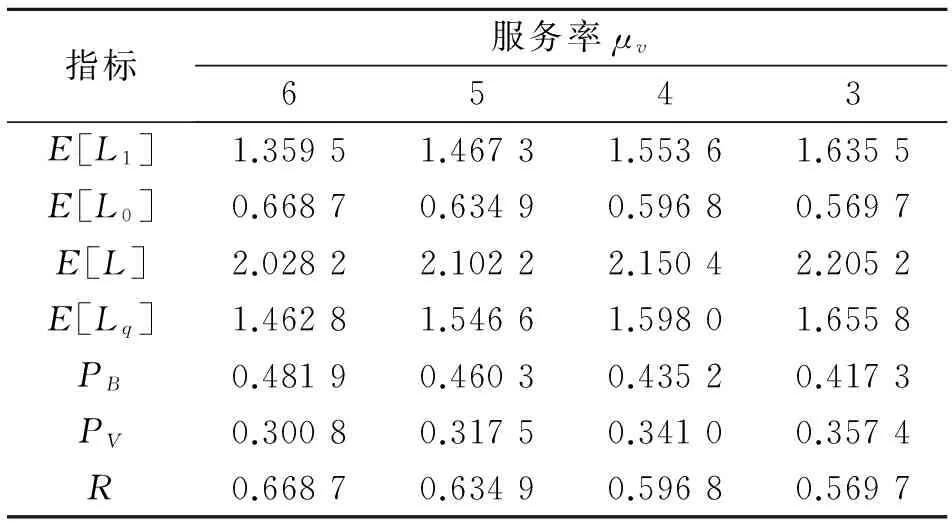
表2 μv取不同值时系统的各项性能指标Tab.2 Performance measures of the system with different μv values

从表1和表2中的结果，可以看出系统的平均队长、平均等待队长、服务员忙的概率随着μb的增加而减少，而服务员休假的概率、顾客平均的中途离去率随着μb的增加而增加；系统的平均队长、平均等待队长、服务员休假的概率随着μv的增加而减少，而服务员忙的概率、顾客平均的中途离去率随着μv的增加而增加.

4 结论

本文提出了具有不耐烦顾客和单重工作休假的M/M/1排队系统模型，利用母函数的方法，求出了忙期和工作休假期的平均队长等性能指标的解析表达式，给出了数值结果并进行分析.

[1] Doshi B T. Single server queues with vacations[C]//Stochastic Analysis of the Computer and Communication Systems.Amsterdam: North-Holland Elsevier,1990:217-264.

[2] Doshi B T. Queueing systems with vacations:a survey[J]. Queueing System,1986, 1(1): 29-66.

[3] Tian N, Zhang Z G. Vacation Queueing Models Theory and Applications[M]. New York: Springer-Verlag, 2006:1-130.

[4] Servi L D, Finn S G.M/M/1 queues with working vacations(M/M/1WV) [J]. Performance Evaluation, 2002, 50(1) : 41-52.

[5] Wu D, Takagi H.M/G/1 queue with multiple working vacation[J]. Performance Evaluation, 2006, 63(7): 654-681.

[6] Baba Y. Analysis of aGI/M/1 queue with multiple working vacations[J]. Operation Research Letters, 2005, 33 (2): 201-209.

[7] Lin C H, Ke J C. Multi-server system with single working vacation[J]. Applied Mathematical Modelling, 2009, 33 (7): 2967-2977.

[8] Altman E, Yechiali U. Analysis of customers’ impatience in queues with server vacations[J]. Queueing System, 2006, 52(1): 261-279.

[9] Yue Dequan, Yue Wuyi, Xu Gang. Analysis of a queueing system with impatient customers and working vacations[C]//Queueing Theory and Network Applications.Seoul,2011:208-212.

TheM/M/1QueuingSystemwiththeImpatientCustomersandSingleWorkingVacation

XU Gang1, YU Yong-bo2

(1.DepartmentofBasicCourses,NortheastPetroleumUniversityatQinhuangdao,Qinhuangdao066004,China; 2.DepartmentofBasicCourses,QinhuangdaoXingrongMaritimeVocationalSchool,Qinhuangdao066100,China)

AnM/M/1 queuing system with impatient customers and single working vacation was considered. When a customer arrived in the system and realized that the server was on vacation, he activated an independent ‘impatient timer’. If the custmer’s service had not been completed before the customer’s timer expired, the customer abandoned the queue, without returning. Some performance measures of the system were derived such as the mean queue sizes in the busy period and in the working vacation period by balance equations and generating functions. The effects of the two service rates on the system performance measures were investigated by numerical experiment.

impatient customers； working vacation； queuing； balance equations； generating functions

2012-08-07

徐刚(1978-)，男，讲师，硕士，主要从事排队论研究，E-mail:xg99228@163.com．

O 226

A

1671-6841(2013)01-0023-04

10.3969/j.issn/1671-6841.2013.01.006